Building a search function is something that every developer has to do. In fact, basic Linear Search functions are usually some of the first patterns that developers learn to write. If you are unfamiliar with this concept I suggest you get up to speed with the basics of Linear Search Algorithms before you dig into Binary Search.

What is Binary Search?

This algorithm allows you to find out if a certain element exists within a larger list. It will help you answer a question like this: Does the number 5 exist in a list of 10, 000 random numbers (that have been sorted)?

Binary search is the most popular Search algorithm.It is efficient and also one of the most commonly used techniques that is used to solve problems. If all the names in the world are written down together in order and you want to search for the position of a specific name, binary search will accomplish this in a maximum of 35 iterations.

It works only on a sorted set of elements. To use binary search on a collection, the collection must first be sorted.

Why do we need this algorithm: the use of binary search significantly speeds up the search for the desired element by reducing the search ranges and therefore is often useful in Big Data.

Let's Learn with some examples:

🚀 Example 1: Find "3"

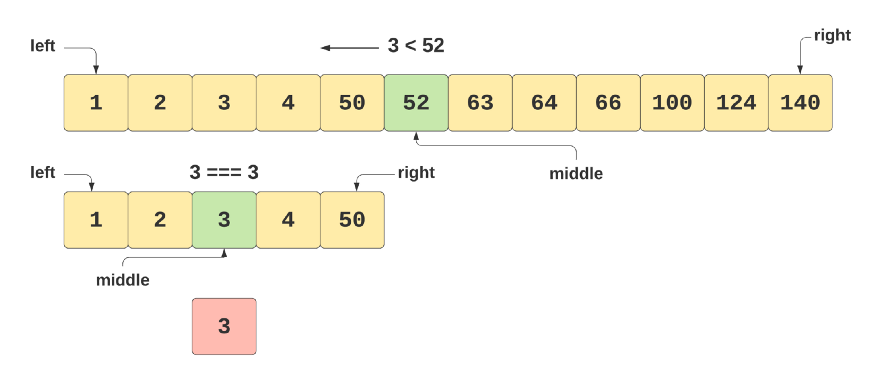
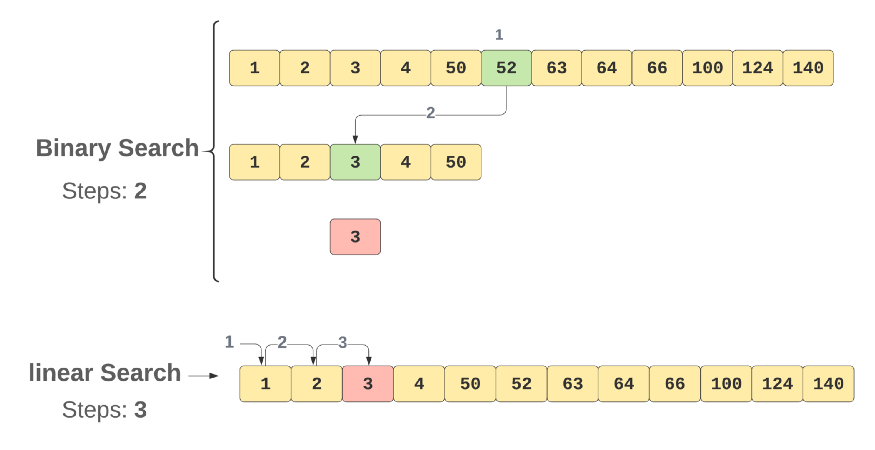
💡 Binary Search: the result will be found in 2 steps | O(Log n);
💡 Linear/Sequential Search: the result will be found in 3 steps | O(n);

🚀 Example 2: Find "124"

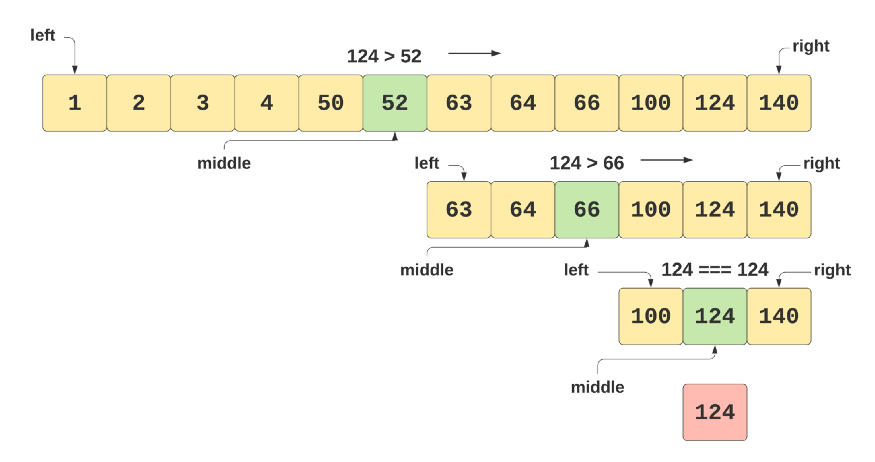
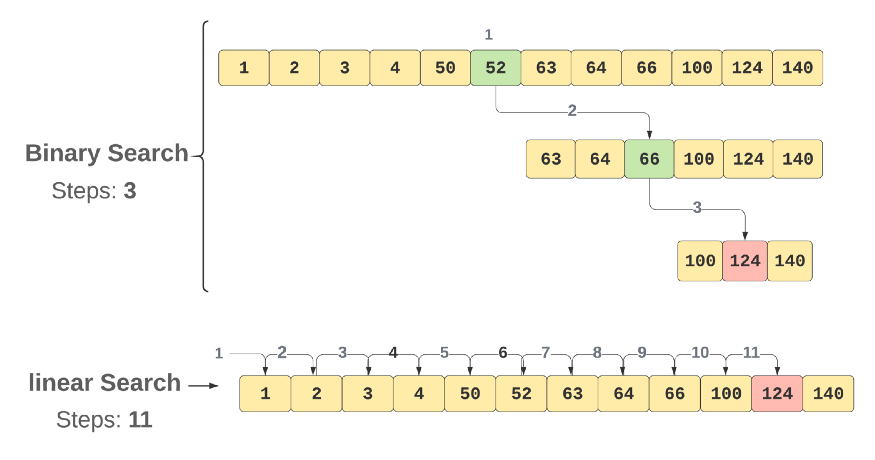
💡 Binary Search: the result will be found in 3 steps | O(Log n);
💡 Linear/Sequential Search: the result will be found in 11 steps | O(n);

Binary Search Logic

The logic behind binary search is:

1. Divide the sorted array in half-half part (lower half and upper half) by using (first index)+(last index)/2

2. Now you will get the index number (middle index) by applying this division

3. Check whether the number present at this index is equal to the number (to be search) or not

4. If it is equal, then stop searching. Print the value of that index where the number is found

5. And if it is not, then check whether the given number is greater than or less than the number present at middle index or not

6. If it is greater than the number present at middle index, then skip the lower half part, and process for the upper half part using the same logic as used from first step. Except, put the value of first index with middle+1. That is, middle+1 replaces the value of first index

7. And if it is less than the number present at middle index, then skip the upper half part, and process for the lower half part using the same logic as used from first step. Except, put the value of last index with middle-1. That is, middle-1 replaces the value of last index

8. Continue checking until the value is found or the interval becomes zero

9. If the value is found, the print the index number as the position of the given number. Otherwise, if interval becomes zero, then print as the number is not found in the array

Implementation

Iterative Function

def binarySearch(arr, l, r, x):
 
    while l <= r:
 
        mid = l + (r - l) // 2;
         
        # Check if x is present at mid
        if arr[mid] == x:
            return mid
 
        # If x is greater, ignore left half
        elif arr[mid] < x:
            l = mid + 1
 
        # If x is smaller, ignore right half
        else:
            r = mid - 1
     
    # If we reach here, then the element
    # was not present
    return -1
 
# Driver Code
arr = [ 2, 3, 4, 10, 40 ]
x = 10
 
# Function call
result = binarySearch(arr, 0, len(arr)-1, x)
 
if result != -1:
    print ("Element is present at index % d" % result)
else:
    print ("Element is not present in array")

Recursive Function

# Returns index of x in arr if present, else -1
 
 
def binarySearch(arr, l, r, x):
 
    # Check base case
    if r >= l:
 
        mid = l + (r - l) // 2
 
        # If element is present at the middle itself
        if arr[mid] == x:
            return mid
 
        # If element is smaller than mid, then it
        # can only be present in left subarray
        elif arr[mid] > x:
            return binarySearch(arr, l, mid-1, x)
 
        # Else the element can only be present
        # in right subarray
        else:
            return binarySearch(arr, mid + 1, r, x)
 
    else:
        # Element is not present in the array
        return -1
 
 
# Driver Code
arr = [2, 3, 4, 10, 40]
x = 10
 
# Function call
result = binarySearch(arr, 0, len(arr)-1, x)
 
if result != -1:
    print("Element is present at index % d" % result)
else:
    print("Element is not present in array")

Time & Space Complexity Analysis

Binary Search is an algorithm is efficiently search an element in a given list of sorted elements. Binary Search reduces the size of data set to searched by half at each step.

Best Case Time Complexity of Binary Search

The best case of Binary Search occurs when: The element to be search is in the middle of the list

In this case, the element is found in the first step itself and this involves 1 comparison.
Therefore, Best Case Time Complexity of Binary Search is O(1).

Average Case Time Complexity of Binary Search

Let there be N distinct numbers: a1, a2, ..., a(N-1), aN. We need to find element P.
There are two cases:

Case 1: The element P can be in N distinct indexes from 0 to N-1.
Case 2: There will be a case when the element P is not present in the list.

There are N case 1 and 1 case 2. So, there are N+1 distinct cases to consider in total.

If element P is in index K, then Binary Search will do K+1 comparisons. This is because the element at index N/2 can be found in 1 comparison as Binary Search starts from middle.

Similarly, in the 2nd comparisons, elements at index N/4 and 3N/4 are compared based on the result of 1st comparison.

Therefore, Elements requiring I comparisons: 2^(I-1)

Total number of comparisons = 1 * (Elements requiring 1 comparison) + 2 * (Elements requiring 2 comparisons) + ... + logN * (Elements requiring logN comparisons)
Total number of comparisons = 1 * (1) + 2 * (2) + 3 * (4) + ... + logN * (2^(logN-1))

Therefore, average number of comparisons = ( N * (logN - 1) + 1 ) / (N+1)
Average number of comparisons = N * logN / (N+1) - N/(N+1) + 1/(N+1)

The dominant term is N * logN / (N+1) which is approximately logN. Therefore, Average Case Time Complexity of Binary Search is O(logN).

Analysis of Worst Case Time Complexity of Binary Search

The worst case of Binary Search occurs when: The element is to search is in the first index or last index

In this case, the total number of comparisons required is logN comparisons. Therefore, Worst Case Time Complexity of Binary Search is O(logN).

Analysis of Space Complexity of Binary Search

In an iterative implementation of Binary Search, the space complexity will be O(1). This is because we need two variable to keep track of the range of elements that are to be checked. No other data is needed.

In a recursive implementation of Binary Search, the space complexity will be O(logN). This is because in the worst case, there will be logN recursive calls and all these recursive calls will be stacked in memory. In fact, if I comparisons are needed, then I recursive calls will be stacked in memory and from our analysis of average case time complexity, we know that the average memory will be O(logN) as well.

Conclusion

The conclusion of our Time and Space Complexity analysis of Binary Search is as follows:

With this article at Logicmojo, you must have the complete idea of analyzing Binary Search algorithm.

Good Luck & Happy Learning!!