Binary Tree from Preorder and Inorder Traversal

Back to home

𝑻𝒂𝒃𝒍𝒆 𝒐𝒇 𝑪𝒐𝒏𝒕𝒆𝒏𝒕

Problem Statement: Construct Binary Tree from Preorder and Inorder Traversal
Approach: Recursion

Logicmojo - Updated Aug 28, 2021

Problem Statement: Construct Binary Tree from Preorder and Inorder Traversal

Given two integer arrays preorder and inorder where preorder is the preorder traversal of a binary tree and inorder is the inorder traversal of the same tree, construct and return the binary tree.

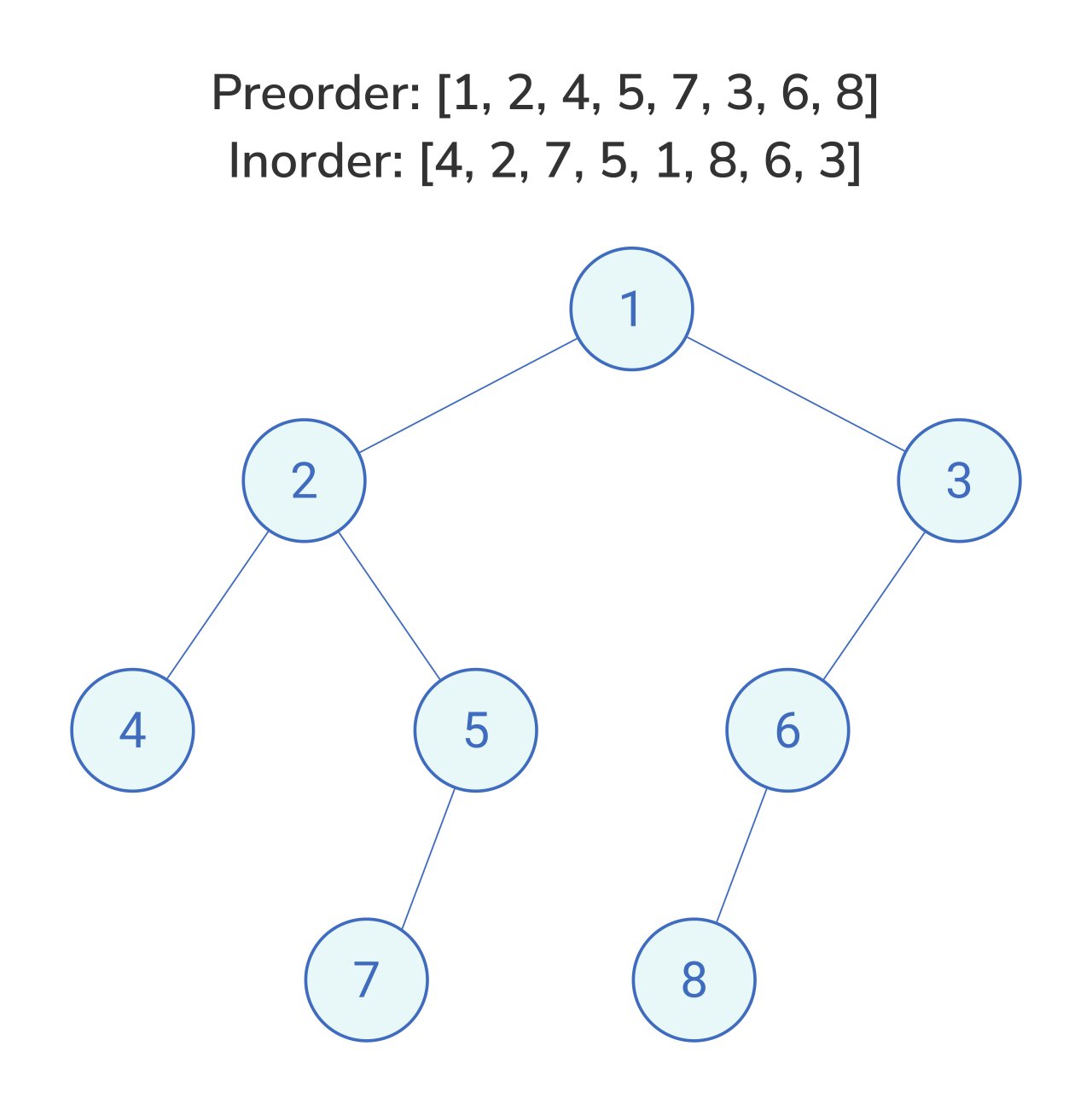
Approach: Recursive

You need to understand preorder and inorder traversal first, and then go ahead.

Basic idea is:preorder[0] is the root node of the tree, preorder[x] is a root node of a sub tree

In in-order traversal: When inorder[index] is an item in the in-order traversal, inorder[0]-inorder[index-1] are on the left branch

inorder[index+1]-inorder[size()-1] are on the right branch. if there is nothing on the left, that means the left child of the node is NULL

if there is nothing on the right, that means the right child of the node is NULL

Algorithm:

1. Start from rootIdx 0

2. Find preorder[rootIdx] from inorder, let's call the index pivot

3. Create a new node with inorder[pivot]

4. Create its left child recursively

5. Create its right child recursively

Return the created node.

C++ Implementation:

class Solution {
public:
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int rootIdx = 0;
        return build(preorder, inorder, rootIdx, 0, inorder.size()-1);
    }
    
    TreeNode* build(vector<int>& preorder, vector<int>& inorder, int& rootIdx, int left, int right) {
        if (left > right) return NULL;
        int pivot = left;  // find the root from inorder
        while(inorder[pivot] != preorder[rootIdx]) pivot++;
        
        rootIdx++;
        TreeNode* newNode = new TreeNode(inorder[pivot]);
        newNode->left = build(preorder, inorder, rootIdx, left, pivot-1);
        newNode->right = build(preorder, inorder, rootIdx, pivot+1, right);
        return newNode;
    }
};

Python Implementation:

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
class Solution:
    def buildTree(self, preorder, inorder):
        def construct(preorder, inorder):
            if inorder:
                root = TreeNode(preorder.pop(0))
                index = inorder.index(root.val)
                root.left = construct(preorder, inorder[:index])
                root.right = construct(preorder, inorder[index + 1:])
                return root
        return construct(preorder, inorder)
def traverse(root):
    if not root:    return root
    traverse(root.left)
    print(root.val, end = ' ')
    traverse(root.right)
if __name__=='__main__':
    ob1 = Solution()
    in_order = [ 9, 8, 4, 2, 10, 5, 10, 1, 6, 3, 13, 12, 7 ]
    pre_order = [ 1, 2, 4, 8, 9, 5, 10, 10, 3, 6, 7, 12, 13 ]
    root = ob1.buildTree(pre_order, in_order)
    traverse(root)
    print()

Time Compexity: O(n²)

Space Compexity: O(n)

With this article at Logicmojo, you must have the complete idea of solving Construct Binary Tree from Preorder and Inorder Traversal problem.