Bit Manipulation for Beginners
Back to home
- Introduction to Bits
- Basics of Bit Manipulation
- Applications of Bit Operations
- Common Bit Tasks
- Bit Tricks
- Commonly Interview Questions
π»ππππ ππ πͺππππππ
Logicmojo - Jan 2, 2023
Computers do not understand words and numbers the way we do. All the data it receives are encoded at the lowest level to a series of zeros and ones. (0 and 1), and this is the only way it makes sense of any command itβs given. This series of 0 and 1 are known as bits.
Working on bytes, or data types comprising of bytes like ints, floats, doubles or even data structures which stores large amount of bytes is normal for a programmer. In some cases, a programmer needs to go beyond this - that is to say that in a deeper level where the importance of bits is realized. Computer programming tasks that require bit manipulation include low-level device control, error detection and correction algorithms, data compression, encryption algorithms, and optimization. For most other tasks, modern programming languages allow the programmer to work directly with abstractions instead of bits that represent those abstractions. Source code that does bit manipulation makes use of the bitwise operations: AND, OR, XOR, NOT, and bit shifts.
Introduction to Bits
Bit stands for Binary Digit, a basic and smallest unit of data in a computer. Binary representation is based on 1s and 0s. A Bit represents a logical state with only 2 boolean values, either 0 or 1, as they are a 2 base number. They are the lowest level of language used in machines.
Basics of Bit manipulation
There are different bitwise operations used in the bit manipulation. These bit operations operate on the individual bits of the bit patterns. Bit operations are fast and can be used in optimizing time complexity. Some common bit operators are:
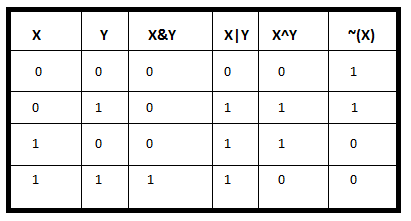
NOT ( ~ ): Bitwise NOT is an unary operator that flips the bits of the number i.e., if the ith bit is 0, it will change it to 1 and vice versa. Bitwise NOT is nothing but simply the oneβs complement of a number. Lets take an example.
N = 5 = (101)2
~N = ~5 = ~(101)2 = (010)2 = 2
AND ( & ): Bitwise AND is a binary operator that operates on two equal-length bit patterns. If both bits in the compared position of the bit patterns are 1,
the bit in the resulting bit pattern is 1, otherwise 0.
A = 5 = (101)2 , B = 3 = (011)2
A & B = (101)2 & (011)2= (001)2 = 1
OR ( | ): Bitwise OR is also a binary operator that operates on two equal-length bit patterns, similar to bitwise AND.
If both bits in the compared position of the bit patterns are 0, the bit in the resulting bit pattern is 0, otherwise 1.
A = 5 = (101)2 , B = 3 = (011)2
A | B = (101)2 | (011)2 = (111)2 = 7
XOR ( ^ ): Bitwise XOR also takes two equal-length bit patterns. If both bits in the compared position of the bit patterns are 0 or 1,
the bit in the resulting bit pattern is 0, otherwise 1.
A = 5 = (101)2 , B = 3 = (011)2
A ^ B = (101)2 ^ (011)2 = (110)2 = 6
Left Shift ( << ): Left shift operator is a binary operator which shift the some number of bits, in the given bit pattern, to the left and append 0 at the end.
Left shift is equivalent to multiplying the bit pattern with ( if we are shifting k bits ).
1 << 1 = 2 = 21
1 << 2 = 4 = 22 1 << 3 = 8 = 23
1 << 4 = 16 = 24
1 << n = 2n
Right Shift ( >> ): Right shift operator is a binary operator which shift the some number of bits, in the given bit pattern, to the right and append 1 at the end.
Right shift is equivalent to dividing the bit pattern with 2k ( if we are shifting k bits ).
4 >> 1 = 2
6 >> 1 = 3
5 >> 1 = 2
16 >> 4 = 1
Applications of bit operations:
1. They are widely used in areas of graphics ,specially XOR(Exclusive OR) operations.
2. They are widely used in the embedded systems, in situations, where we need to set/clear/toggle just one single bit of a specific register without modifying the other contents. We can do OR/AND/XOR operations with the appropriate mask for the bit position.
3. Data structure like n-bit map can be used to allocate n-size resource pool to represent the current status.
4. Bits are used in networking, framing the packets of numerous bits which is sent to another system generally through any type of serial interface.
Common Bit Tasks
πSet Bit: Set bits in a binary number is represented by 1. Whenever we calculate the binary number of an integer value then it is formed as the combination of 0's and 1's. So, the digit 1 is known as set bit in the terms of the computer.
int setBit(int num, int position) {
int mask = 1 << position;
return x | mask;
}
πGet Bit:
boolean getBit(int num, int position) {
return ((num & (1 << i)) != 0);
}
πClear Bit:
int clearBit(int num, int position) {
int mask = 1 << position;
return x & ~mask;
}
πUpdate Bit:
int updateBit(int num, int position, boolean isOne) {
int value = isOne? 1:0;
int mask = ~(1 << i)l
return (num & mask) | (value << i);
}
Bit Tricks
Check if a given number is even?
if the least bit is 0, this can be done by using the bit-wise AND
(x & 1 ) == 0
0110 (6)
& 0001
= 0000 TRUE
Check if the number is a power of 2?
a number that is a power of two, should only have one 1 set; if we subtract 1, all the zeros following will be set to one. If we & that with the original number we get 0
(x & x-1) == 0
Division by power of 2
num = num >> i; //division by pow(2,i)
Suppose an example
8= 1000(binary)
8/pow(2,1)=4 = 0100 (shifed all bits one position to right if we compare with 1000)=8>>1 (right shift by 1)
8/pow(2,2)=2 = 0010 (shifted all bits two position to right if we compare with 1000 )=8>>2 (right shift by 2)
To Swap two numbers
x = x ^ y;
y = x ^ y;
x = x ^ y;
Approach
x = x ^ y -------------------------- eq. 1
y = x ^ y --------------------------eq. 2
x = x ^ y ---------------------------eq. 3
put the value of x from eq. 1 to eq. 2 we got
y = (x ^ y) ^ y = x ^ (y ^ y) = x ^ 0 = x ..... we got y = x ----------eq 4
put the value of y from eq. 4 and x from eq. 1 to eq. 3 we got
x = (x ^ y) ^ x = (x ^ x) ^ y = 0 ^ y = y ...... we got x = y -----------eq 5
according to eq 4 and eq 5
y = x
x = y
hence x and y are swapped
Find max min of two numbers
minimum = y ^ ((x ^ y) & -(x < y)); // min(x, y)
maximum = x ^ ((x ^ y) & -(x < y)); // max(x, y)
Approach
if x < y holds, then -(x < y) will be -1 which is all ones(11111β¦.)
so minimum = y ^ ((x ^ y) & (111111β¦)) = y ^ x ^ y = x.
And if x>y holds , then-(x
How to count the number of set bits in a number?
We can keep removing the LSB, until the number becomes zero, while doing so, we will keep a count on number of bits removed, the final count will be the number of set bits.
int c=0;
while(n>0){
n=n&(n-1);
c++;
}
print(c)
Complexity : O(number of set bits).
Subset Generation
Bit Manipulation can help us iterate over or generate all the possible (2^n) subset of a given array (of size n). Basically, we use the idea that we can represent a subset of the array as 0βs and 1βs , there will be total n bits, β1β at the ith bit indicates that the ith element is chosen for the current subset, and 0 indicates that it is not chosen, like if there are 3 (n=3) elements , 110 would indicate zeroth index element is not chosen (0), 1st index element is chosen (1), and 2nd element is also chosen(1), we do the same for all other 3 bit binary numbers too like 101,001,111,etc.
Implementation:
int ar[]={1,2,3};
int n = len(arr); //=3
for(int i = 0;i < (1 << n);i++){
for(int j = 0;j < n;++j){
if(i & (1 << j))
cout << ar[j] << ' ';
}
cout << endl;
}
Complexity : O(n * 2^n)
Commonly Interview Questions
1. Find the missing number in an array without using any extra space
2. Compute modulus division without division and modulo operator
3. Reverse bits of an integer
4. Find the odd occurring element in an array
5. Find XOR of two numbers without using the XOR operator
6. Conditionally negate a value without branching
Good luck and happy learning!