Bottom View of Binary Tree

Back to home
Logicmojo - Updated Aug 28, 2021



Problem Statement: Bottom View of Binary Tree

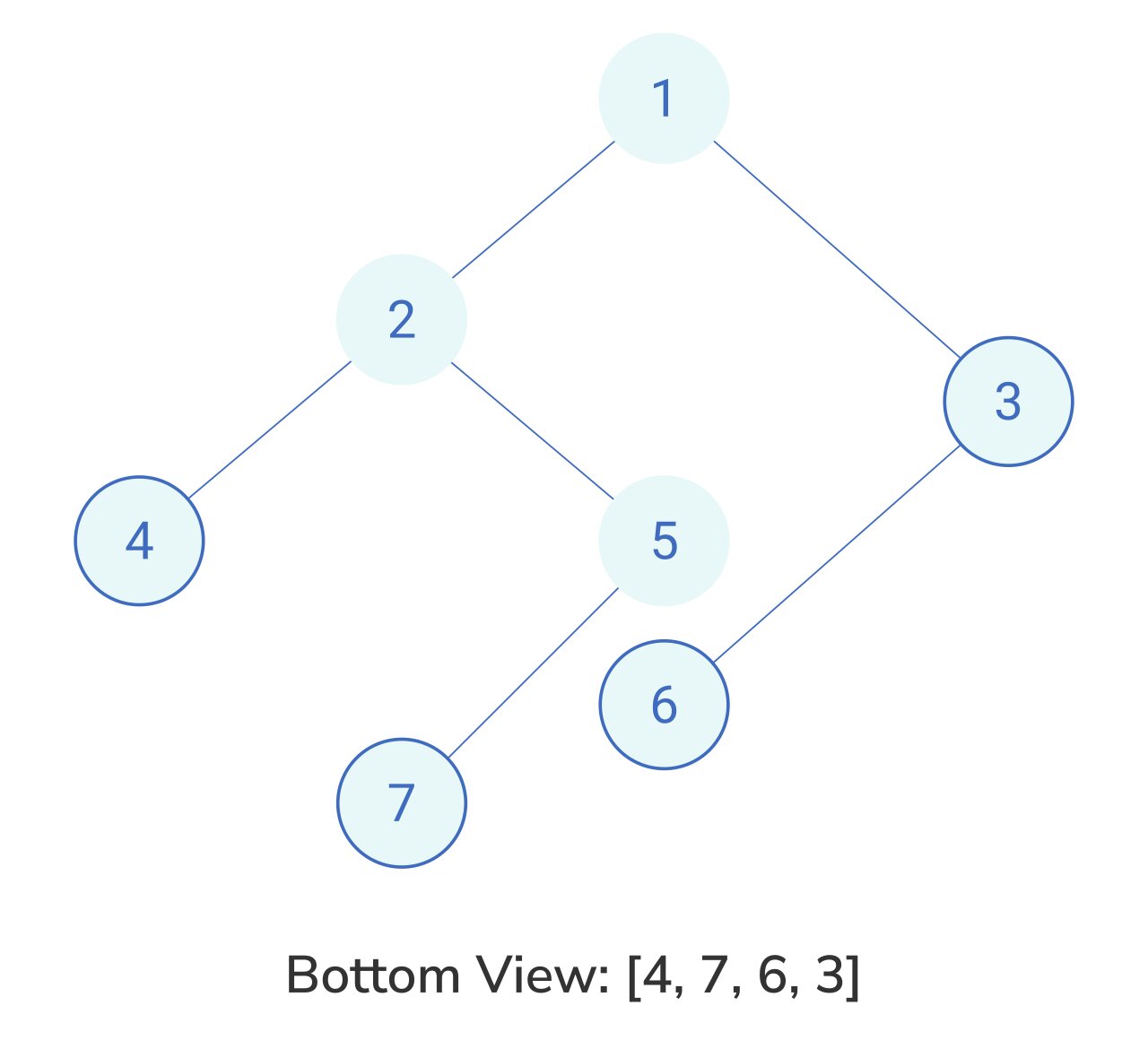
There are different ways to look at a binary tree. The bottom view of a binary tree contains the set of nodes that will be visible if you look at the binary tree from the bottom.


Note: If there are multiple bottom-most nodes for a horizontal distance from root, use the later one in level-order traversal.


Given the root node of a binary tree, return an array containing the node elements in the bottom view, from left to right.


Approach Recursive

The bottom view of a binary tree refers to the bottommost nodes present at their horizontal distance.

For the nodes of a binary tree, the horizontal distance is defined as follows.

Horizontal distance of the root = 0

Horizontal distance of a left child = horizontal distance of its parent - 1

Horizontal distance of a right child = horizontal distance of its parent + 1


Algorithm

1. Perform pre-order traversal to calculate the horizontal distance of each node.

2. For each node add the node to the result if it is the first node to have a particular horizontal distance.

3. If a node exists in the result for a particular edit distance, then only replace that node with the present node if the present node is at a level greater than that of the already added node.


C++ Implementation:

#include <iostream>
#include <map>
using namespace std;
 
// Data structure to store a binary tree node
struct Node
{
    int key;
    Node *left, *right;
 
    Node(int key)
    {
        this->key = key;
        this->left = this->right = nullptr;
    }
};
 
// Recursive function to perform preorder traversal on the tree and fill the map.
// Here, the node has `dist` horizontal distance from the tree's root,
// and the `level` represents the node's level.
 
void printBottom(Node* node, int dist, int level, auto &map)
{
    // base case: empty tree
    if (node == nullptr) {
        return;
    }
 
    // if the current level is more than or equal to the maximum level seen so far
    // for the same horizontal distance or horizontal distance is seen for
    // the first time, update the map
 
    if (level >= map[dist].second)
    {
        // update value and level for the current distance
        map[dist] = { node->key, level };
    }
 
    // recur for the left subtree by decreasing horizontal distance and
    // increasing level by 1
    printBottom(node->left, dist - 1, level + 1, map);
 
    // recur for the right subtree by increasing both level and
    // horizontal distance by 1
    printBottom(node->right, dist + 1, level + 1, map);
}
 
// Function to print the bottom view of a given binary tree
void printBottom(Node* root)
{
    // create an empty map where
    // key —> relative horizontal distance of the node from the root node, and
    // value —> pair containing the node's value and its level
 
    map<int, pair<int, int>> map;
 
    // perform preorder traversal on the tree and fill the map
    printBottom(root, 0, 0, map);
 
    // traverse the map and print the bottom view
    for (auto it: map) {
        cout << it.second.first << " ";
    }
}
 
int main()
{
    Node* root = new Node(1);
    root->left = new Node(2);
    root->right = new Node(3);
    root->left->right = new Node(4);
    root->right->left = new Node(5);
    root->right->right = new Node(6);
    root->right->left->left = new Node(7);
    root->right->left->right = new Node(8);
 
    printBottom(root);
 
    return 0;
}


Python Implementation:

class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None

def bottom_view(root, dist_val, level = 0, dist = 0):
    if root:
        bottom_view(root.left, dist_val, level + 1, dist - 1)
        if dist not in dist_val or level >= dist_val[dist][1]:
                dist_val[dist] = [root.val, level]
        bottom_view(root.right, dist_val, level + 1, dist + 1)

if __name__=='__main__':
    root = Node(1)
    root.left = Node(2)
    root.right = Node(3)
    root.left.right = Node(4)
    root.right.left = Node(5)
    root.right.right = Node(6)
    root.right.left.left = Node(7)
    root.right.left.right = Node(8)
    dist_val = {}
    bottom_view(root, dist_val)
    for dist in dist_val:
        print(dist_val[dist][0])

Time-Complexity: O(n)

Auxiliary Space: O(n)

With this article at Logicmojo, you must have the complete idea of solving Bottom View of Binary Tree problem.
© 2020 Logicmojo. ALL RIGHTS RESERVED