 Logicmojo - Updated Sept 18, 2021
Logicmojo - Updated Sept 18, 2021
The Bubble Sort gets its name because elements tend to move up into the correct order like bubbles rising to the surface. Bubble Sort is the simplest sorting algorithm that works by repeatedly swapping adjacent elements in an array when a condition is met. For example, a simple bubble sort function would be to numerically order the elements in an array from least to greatest.
It also referred to as comparison sort, is a simple sorting algorithm that repeatedly goes through the list, compares adjacent elements and swaps them if they are in the wrong order. This is the most simplest algorithm and inefficient at the same time. Yet, it is very much necessary to learn about it as it represents the basic foundations of sorting.
Bubble Sort Algorithm: Steps on how it works:
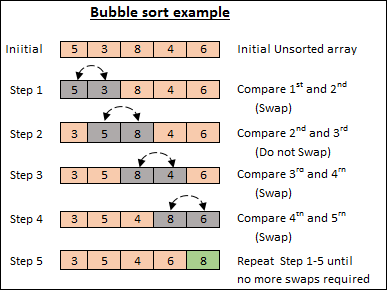
1. In an unsorted array of 5 elements, start with the first two elements and sort them in ascending order. (Compare the element to check which one is greater).
2. Compare the second and third element to check which one is greater, and sort them in ascending order.
3. Compare the third and fourth element to check which one is greater, and sort them in ascending order.
4. Compare the fourth and fifth element to check which one is greater, and sort them in ascending order.
5. Repeat steps 1–5 until no more swaps are required.
Below is an image of an array, which needs to be sorted. We will use the Bubble Sort Algorithm, to sort this array:

Algorithm
bubbleSort(array)
for i <- 1 to indexOfLastUnsortedElement-1
if leftElement > rightElement
swap leftElement and rightElement
end bubbleSort
Characteristics of Bubble Sort
1. Large values are always sorted first.
2. It only takes one iteration to detect that a collection is already sorted.
3. The best time complexity for Bubble Sort is O(n). The average and worst time complexity is O(n²).
4. The space complexity for Bubble Sort is O(1), because only single additional memory space is required.
Implementation in Python
# Bubble sort in Python def bubbleSort(array): # loop to access each array element for i in range(len(array)): # loop to compare array elements for j in range(0, len(array) - i - 1): # compare two adjacent elements # change > to < to sort in descending order if array[j] > array[j + 1]: # swapping elements if elements # are not in the intended order temp = array[j] array[j] = array[j+1] array[j+1] = temp data = [-2, 45, 0, 11, -9] bubbleSort(data) print('Sorted Array in Ascending Order:') print(data)
Implementation in C++
// Bubble sort in C++ #include <iostream> using namespace std; // perform bubble sort void bubbleSort(int array[], int size) { // loop to access each array element for (int step = 0; step < size; ++step) { // loop to compare array elements for (int i = 0; i < size - step; ++i) { // compare two adjacent elements // change > to < to sort in descending order if (array[i] > array[i + 1]) { // swapping elements if elements // are not in the intended order int temp = array[i]; array[i] = array[i + 1]; array[i + 1] = temp; } } } } // print array void printArray(int array[], int size) { for (int i = 0; i < size; ++i) { cout << " " << array[i]; } cout << "\n"; } int main() { int data[] = {-2, 45, 0, 11, -9}; // find array's length int size = sizeof(data) / sizeof(data[0]); bubbleSort(data, size); cout << "Sorted Array in Ascending Order:\n"; printArray(data, size); }
Optimized Bubble Sort Algorithm
In the above algorithm, all the comparisons are made even if the array is already sorted. This increases the execution time.
To solve this, we can introduce an extra variable swapped. The value of swapped is set true if there occurs swapping of elements. Otherwise, it is set false.
After an iteration, if there is no swapping, the value of swapped will be false. This means elements are already sorted and there is no need to perform further iterations.
This will reduce the execution time and helps to optimize the bubble sort.
bubbleSort(array)
swapped <- false
for i <- 1 to indexOfLastUnsortedElement-1
if leftElement > rightElement
swap leftElement and rightElement
swapped <- true
end bubbleSort
Implementation in Python
# Optimized Bubble sort in Python def bubbleSort(array): # loop through each element of array for i in range(len(array)): # keep track of swapping swapped = False # loop to compare array elements for j in range(0, len(array) - i - 1): # compare two adjacent elements # change > to < to sort in descending order if array[j] > array[j + 1]: # swapping occurs if elements # are not in the intended order temp = array[j] array[j] = array[j+1] array[j+1] = temp swapped = True # no swapping means the array is already sorted # so no need for further comparison if not swapped: break data = [-2, 45, 0, 11, -9] bubbleSort(data) print('Sorted Array in Ascending Order:') print(data)
Implementation in C++
// Optimized bubble sort in C++ #include using namespace std; // perform bubble sort void bubbleSort(int array[], int size) { // loop to access each array element for (int step = 0; step < (size-1); ++step) { // check if swapping occurs int swapped = 0; // loop to compare two elements for (int i = 0; i < (size-step-1); ++i) { // compare two array elements // change > to < to sort in descending order if (array[i] > array[i + 1]) { // swapping occurs if elements // are not in intended order int temp = array[i]; array[i] = array[i + 1]; array[i + 1] = temp; swapped = 1; } } // no swapping means the array is already sorted // so no need of further comparison if (swapped == 0) break; } } // print an array void printArray(int array[], int size) { for (int i = 0; i < size; ++i) { cout << " " << array[i]; } cout << "\n"; } int main() { int data[] = {-2, 45, 0, 11, -9}; // find the array's length int size = sizeof(data) / sizeof(data[0]); bubbleSort(data, size); cout << "Sorted Array in Ascending Order:\n"; printArray(data, size); }
Time & Space Complexity Analysis
Best case scenario: The best case scenario occurs when the array is already sorted. In this case, no swapping will happen in the first iteration (The swapped variable will be false). So, when this happens, we break from the loop after the very first iteration. Hence, time complexity in the best case scenario is O(n) because it has to traverse through all the elements once.
Worst case and Average case scenario: In Bubble Sort, n-1 comparisons are done in the 1st pass, n-2 in 2nd pass, n-3 in 3rd pass and so on. So, the total number of comparisons will be:
Sum = (n-1) + (n-2) + (n-3) + ..... + 3 + 2 + 1
Sum = n(n-1)/2
Hence, the time complexity is O(n2).
Space Complexity of Bubble sort
The space complexity for the algorithm is O(1), because only a single additional memory space is required i.e. for temporary variable used for swapping.
With this article at Logicmojo, you must have the complete idea of analyzing Bubble Sort algorithm.
Good Luck & Happy Learning!!
