Combination Sum

Back to home

𝑻𝒂𝒃𝒍𝒆 𝒐𝒇 𝑪𝒐𝒏𝒕𝒆𝒏𝒕

Problem Statement: Combination Sum
Approach: Backtracking

Logicmojo - Updated Aug 28, 2021

Problem Statement: Combination Sum

Given an array of distinct integers candidates and a target integer target, return a list of all unique combinations of candidates where the chosen numbers sum to target. You may return the combinations in any order.

Example:

arr = [2,3,5], target = 8

Output: [[2,2,2,2],[2,3,3],[3,5]]

Approach: Backtracking

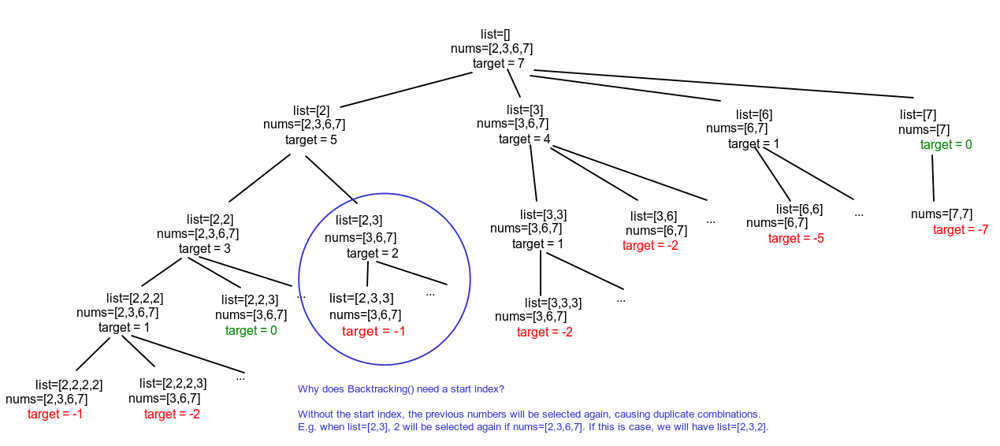
The approach for the problem is simple to find. Generally, in problems such as this, we are required to use backtracking. Because in such questions we are required to do a complete search and find the answer.

Algorithm:

1. If target == 0, it means we found solution, which is kept in curr_sol, so we add it to solution list of all found solutions.

2. If target if negative or k is more than number of candidates, we need to go back.

3. Finally, for each candidate index in k,..., we run our function recursively with updated parameters.

C++ Implementation:

#include<bits/stdc++.h>

using namespace std;
class Solution {
  public:
    void findCombination(int ind, int target, vector < int > & arr, vector < vector < int >> & ans, vector < int > & ds) {
      if (ind == arr.size()) {
        if (target == 0) {
          ans.push_back(ds);
        }
        return;
      }
      // pick up the element 
      if (arr[ind] <= target) {
        ds.push_back(arr[ind]);
        findCombination(ind, target - arr[ind], arr, ans, ds);
        ds.pop_back();
      }

      findCombination(ind + 1, target, arr, ans, ds);

    }
  public:
    vector < vector < int >> combinationSum(vector < int > & candidates, int target) {
      vector < vector < int >> ans;
      vector < int > ds;
      findCombination(0, target, candidates, ans, ds);
      return ans;
    }
};
int main() {
  Solution obj;
  vector < int > v {2,3,6,7};
  int target = 7;

  vector < vector < int >> ans = obj.combinationSum(v, target);
  cout << "Combinations are: " << endl;
  for (int i = 0; i < ans.size(); i++) {
    for (int j = 0; j < ans[i].size(); j++)
      cout << ans[i][j] << " ";
    cout << endl;
  }
}

Python Implementation:

class Solution:
    def combinationSum(self, candidates, target):
        def BackTr(target, curr_sol, k):  
            if target == 0:
                self.sol.append(curr_sol)

            if target < 0 or k >= len(candidates):
                return

            for i in range(k, len(candidates)):
                BackTr(target - candidates[i], curr_sol + [candidates[i]], i)
        
        self.sol = []
        BackTr(target, [], 0)   
        return self.sol
ob1 = Solution()
print(ob1.combinationSum([2,3,5], 8))

Time Complexity: O(n^k) where n is the length of the array and k is the length of the longest possible combination

Space Complexity: O(k), for storing the path, which could be k long at most.

With this article at Logicmojo, you must have the complete idea of solving Combination Sum problem.