Sorting is a near ubiquitous process in our daily lives. It makes sense to organize things to better use them. The same can be said for data. In computer programming—and mathematics, for that matter—sorting algorithms are frequently used to order data as needed to perform a calculation, feed an engine, render an interface, etc.

There are several well known sorting algorithms: e.g. bubble, quick, selection, insertion, merge, heap, bucket. There is also a lesser known sorting algorithm, relegated to the proverbial annex like poor Toby: counting sort. Have you ever heard of it? It is infrequently used because it comes with some caveats which make it impractical in most use cases.

What is Counting Sort Algorithm?

Counting sort is a sorting algorithm that sorts the elements with the technique of counting the number of occurrences of each unique element in an array or list. Counting algorithm is basically a hashing technique with the keys between a specific range and then counting the number of objects having distinct key values. Lastly, we will get the output sequence by doing some arithmetic calculation for positioning each object using their key values. Counting sort uses the partial hashing technique to count the occurrence of the element in O(1). The most important feature of working with counting sort is that it works with negative elements also. It uses the subroutine to another sorting algorithm. The counting sort is not a comparison-based sorting algorithm and its time complexity is O(n) with space proportional to the range of elements. Therefore, the efficiency of counting sort is maximum if the range of elements is not greater than the number of elements to be sorted.

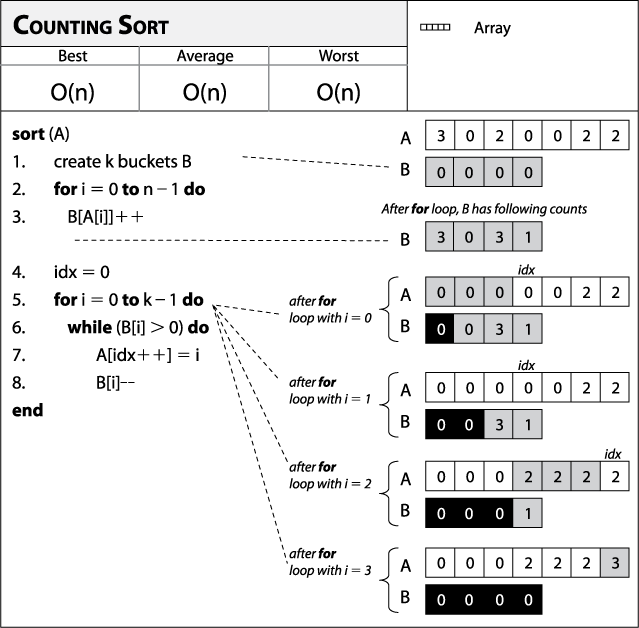
Algorithm of Counting

Implementation in Python

# Counting sort in Python programming


def countingSort(array):
    size = len(array)
    output = [0] * size

    # Initialize count array
    count = [0] * 10

    # Store the count of each elements in count array
    for i in range(0, size):
        count[array[i]] += 1

    # Store the cummulative count
    for i in range(1, 10):
        count[i] += count[i - 1]

    # Find the index of each element of the original array in count array
    # place the elements in output array
    i = size - 1
    while i >= 0:
        output[count[array[i]] - 1] = array[i]
        count[array[i]] -= 1
        i -= 1

    # Copy the sorted elements into original array
    for i in range(0, size):
        array[i] = output[i]


data = [4, 2, 2, 8, 3, 3, 1]
countingSort(data)
print("Sorted Array in Ascending Order: ")
print(data)

Implementation in C++

// Counting sort in C++ programming

#include <iostream>
using namespace std;

void countSort(int array[], int size) {
  // The size of count must be at least the (max+1) but
  // we cannot assign declare it as int count(max+1) in C++ as
  // it does not support dynamic memory allocation.
  // So, its size is provided statically.
  int output[10];
  int count[10];
  int max = array[0];

  // Find the largest element of the array
  for (int i = 1; i < size; i++) {
    if (array[i] > max)
      max = array[i];
  }

  // Initialize count array with all zeros.
  for (int i = 0; i <= max; ++i) {
    count[i] = 0;
  }

  // Store the count of each element
  for (int i = 0; i < size; i++) {
    count[array[i]]++;
  }

  // Store the cummulative count of each array
  for (int i = 1; i <= max; i++) {
    count[i] += count[i - 1];
  }

  // Find the index of each element of the original array in count array, and
  // place the elements in output array
  for (int i = size - 1; i >= 0; i--) {
    output[count[array[i]] - 1] = array[i];
    count[array[i]]--;
  }

  // Copy the sorted elements into original array
  for (int i = 0; i < size; i++) {
    array[i] = output[i];
  }
}

// Function to print an array
void printArray(int array[], int size) {
  for (int i = 0; i < size; i++)
    cout << array[i] << " ";
  cout << endl;
}

// Driver code
int main() {
  int array[] = {4, 2, 2, 8, 3, 3, 1};
  int n = sizeof(array) / sizeof(array[0]);
  countSort(array, n);
  printArray(array, n);
}

Time & Space Complexity Analysis

Counting sort takes O(n+k) time and O(n+k) space, where nn is the number of items we're sorting and k is the number of possible values. We iterate through the input items twice—once to populate counts and once to fill in the output array. Both iterations are O(n) time. Additionally, we iterate through counts once to fill in nextIndex, which is O(k) time. The algorithm allocates three additional arrays: one for counts, one for nextIndex, and one for the output. The first two are O(k) space and the final one is O(n) space.

In many cases cases, k is O(n) (i.e.: the number of items to be sorted is not asymptotically different than the number of values those items can take on. Because of this, counting sort is often said to be O(n) time and space.

With this article at Logicmojo, you must have the complete idea of analyzing Counting Sort algorithm.

Good Luck & Happy Learning!!