Diameter of Binary Tree

Problem Statement: Diameter of Binary Tree

Given a binary tree, return the length of the diameter of the tree. The diameter of a binary tree is the length of the longest path between any two nodes of the tree. The length is the number of edges in the path. The path may or may not include the root node.

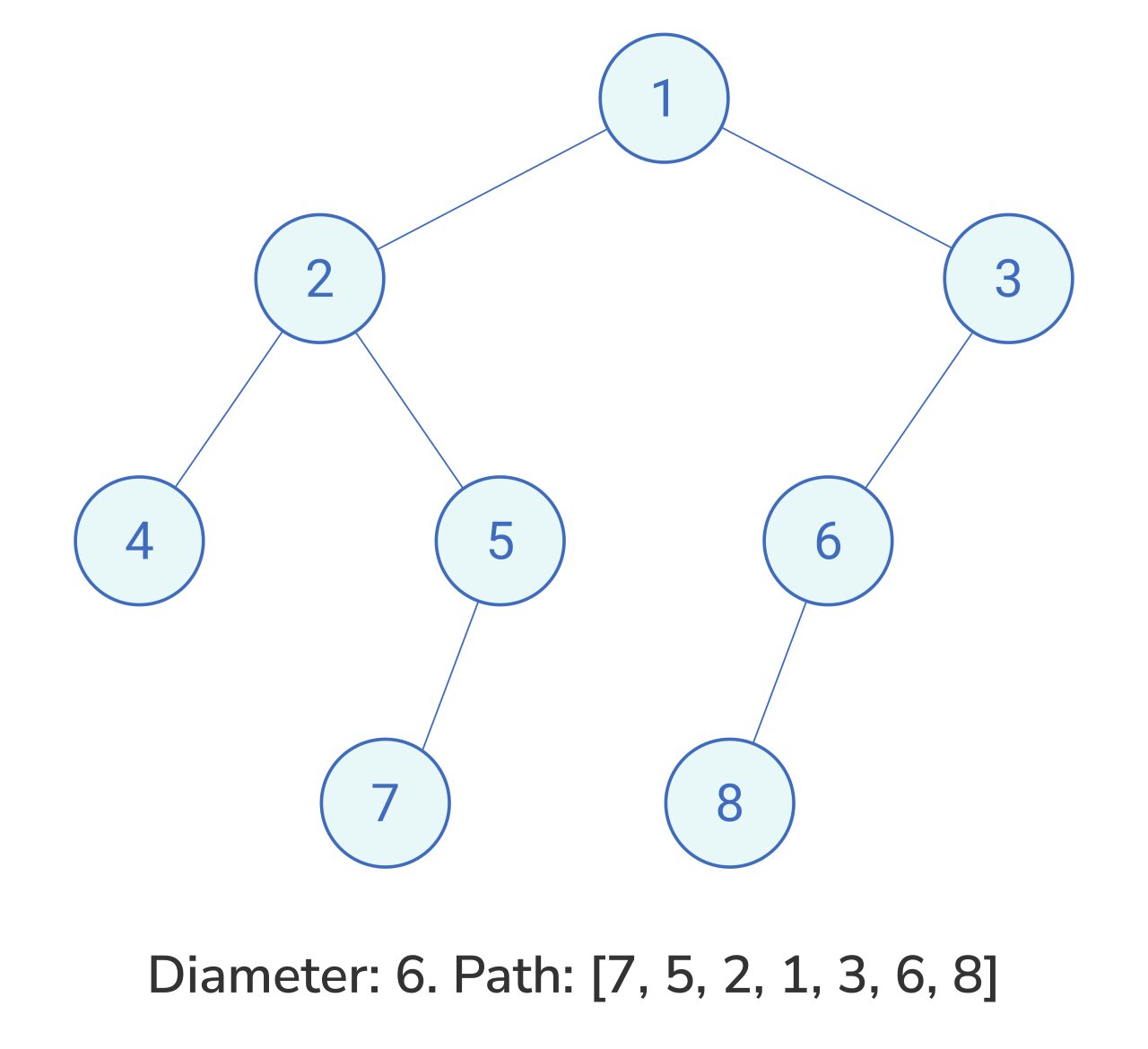
Approach 1: Recursive Approach

There exist two cases, the diameter of every subtree tree may include the sub-root or may not include the sub-root. The diameter of the sub-tree is certainly the maximum sum of the left height and the right height for a sub-root node.

Let’s calculate the depth of a tree for a root TreeNode. The Maximum Depth of Binary Tree problem has a solution that shows how to do this.

If at a root node (without using parents), the diameter is the maximum of either:

1. Max depth for Left Subtree + max depth for right subtree

2. The diameter of Left subtree (without using this sub root TreeNode)

3. The diameter of Right subtree (without using this sub root TreeNode)

We visit every TreeNode recursively and calculate (1), saving the largest value we've found in max. Since we calculate this value for every TreeNode, we have indirectly calculated (2) and (3) as well. Our solution is the final value for max.

class Solution {
public:
    int diameterOfBinaryTree(TreeNode* root) {
        int diameter = 0;
        height(root, diameter);
        return diameter;
    }

private:
    int height(TreeNode* node, int& diameter) {

        if (!node) {
            return 0;
        }

        int lh = height(node->left, diameter);
        int rh = height(node->right, diameter);

        diameter = max(diameter, lh + rh);

        return 1 + max(lh, rh);
    }
};

class Node:
    def __init__(self, val):
        self.val = val
        self.left = None
        self.right = None

def height(root):
    if not root:
        return 0
    return 1 + max(height(root.left), height(root.right))

def diameter(root, dia = 0):
    if root:
        dia = max(dia, 1 + height(root.left) + height(root.right))
        dia = diameter(root.left, dia)
        dia = diameter(root.right, dia)
    return dia

if __name__=='__main__':
    root = Node(1)
    root.left = Node(2)
    root.right = Node(3)
    root.left.right = Node(4)
    root.right.left = Node(5)
    root.right.right = Node(6)
    root.right.left.left = Node(7)
    root.right.left.right = Node(8)
    dia = diameter(root)
    print(dia)

Time Complexity:O(n), since we must visit each node.

Space Complexity: O(log n), if a balanced tree, O(n) otherwise. Space complexity is due to recursion.