Dijkstra’s Algorithm
 Logicmojo - Updated Sept 18, 2021
Logicmojo - Updated Sept 18, 2021
Imagine that you’re traveling to N cities and what if you want save some time and fuel? You have to calculate the shortest distance to that city. Don’t worry, a Dutch scientist, Dijkstra, has discovered a trick to make your life easier.It’s called Dijkstra’s Algorithm. This is a very important algorithm that will boost up your competitive coding skills and also help you face your interview may be
What is this Dijkstra’s algorithm?
Dijkstra’s algorithm is an algorithm for finding the shortest paths between nodes in a graph, which may represent, for example, road maps. It was derived by a computer scientist Edsger W. Dijkstra in 1956. The best example to depict the application of Dijkstra’s algorithm is Google Maps. It gives you number of ways from one destination to the other. But, it primarily focuses on the shortest path between the 2 places.
Algorithm
Now let’s see the algorithm step by step:
1. First of all, we will mark all vertex as unvisited vertex
2. Then, we will mark the source vertex as 0 and all other vertices as infinity
3. Consider source vertex as current vertex
4. Calculate the path length of all the neighboring vertex from the current vertex by adding the weight of the edge in the current vertex
5. Now, if the new path length is smaller than the previous path length then replace it otherwise ignore it
6. Mark the current vertex as visited after visiting the neighbor vertex of the current vertex
7. Select the vertex with the smallest path length as the new current vertex and go back to step 4.
8. Repeat this process until all the vertex are marked as visited.
To explain how this algorithm works first I need to show you the graph that we are going to use in the rest of this section:
1. Step 1: We begin with the list of visited vertices empty and all the nodes in the list of unvisited vertices. The distance from A to A is 0. The shortest distance to all other vertices is infinity. The current vertex is set to A.
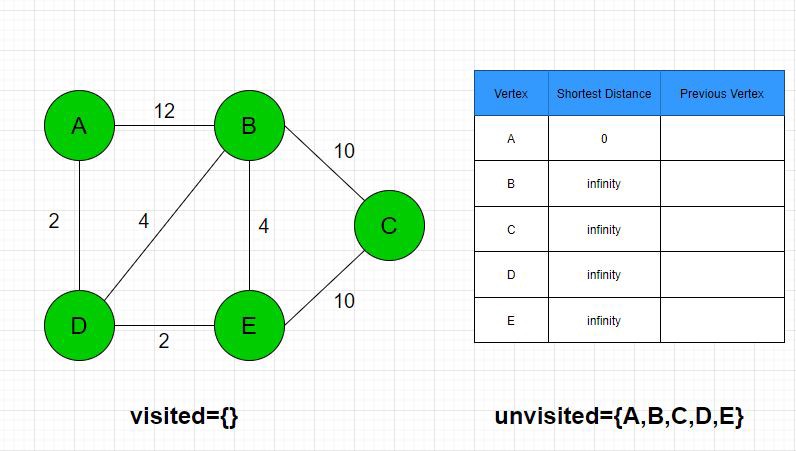
Step 2: A’s unvisited neighbors are B and D. The distance to B and D through A are 0 + 12 = 12 and 0 + 2 = 2 respectively. These are shorter than infinity and thus set to the new shortest distances. A is added to the list of visited vertices. Both distances change; therefore, A is set to the previous vertex for B and D. D has the shortest distance and is set to the next current node.
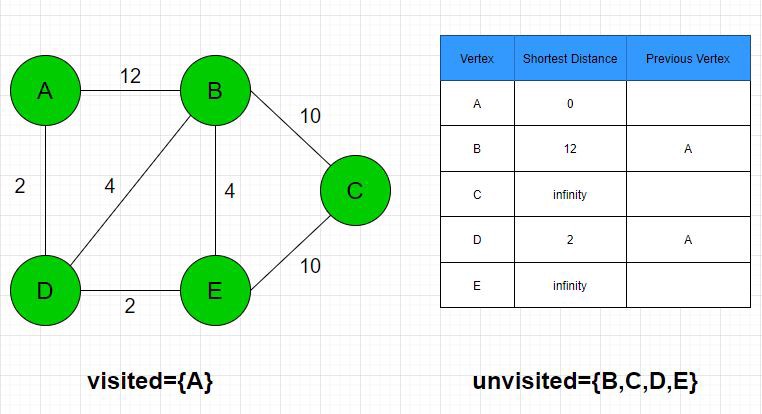
3. Step 3: D’s unvisited neighbors are B and E. The distance to B and E through D are 2 + 4= 6 and 2 + 2 = 4 respectively. The B node distance is changed to 6, and E’s distance is changed to 4 as both are lower distances. D is added to the list of visited vertices and as the previous vertex for B and E. The new shortest distance for the D’s neighbors is 4. E is now the new current node.
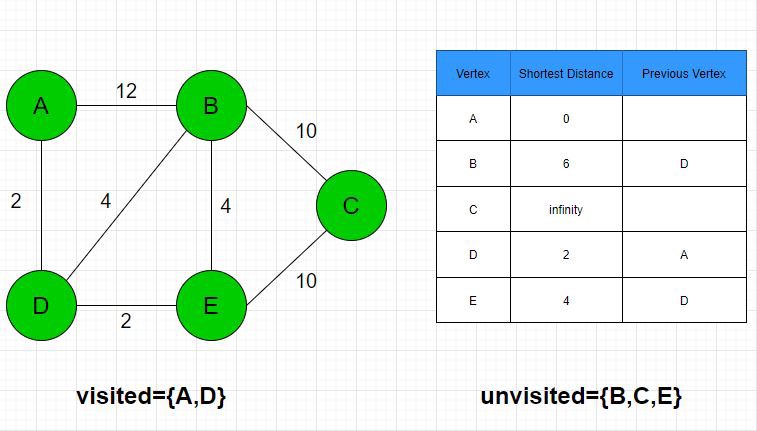
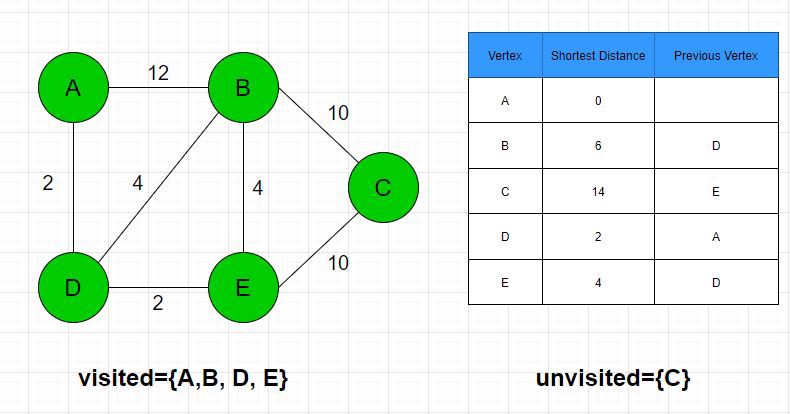
4. Step 4: E’s unvisited neighbors are B and C. The distance to B and C through E are 4+ 4= 8 and 4+ 10= 14, respectively. The distance to C is changed to 14. E is added as C’s previous vertex. The new shortest distance for the E’s neighbors is 6. B is now the new current node.
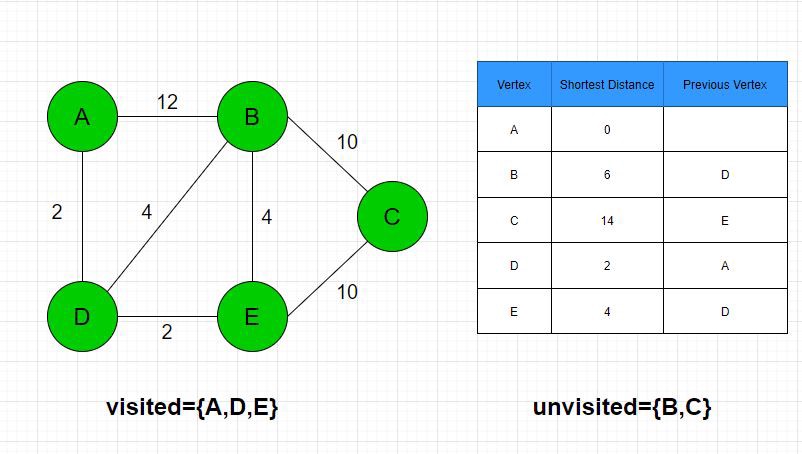
Step 5: B’s only remaining unvisited neighbor is C. The distance to C through B is 6+ 10= 16. Nothing is changed. C is set to the current node. However, it has no unvisited vertice neighbors left, so the algorithm returns the table information and ceases.
Implementation in Python
# Dijkstra's Algorithm in Python import sys # Providing the graph vertices = [[0, 0, 1, 1, 0, 0, 0], [0, 0, 1, 0, 0, 1, 0], [1, 1, 0, 1, 1, 0, 0], [1, 0, 1, 0, 0, 0, 1], [0, 0, 1, 0, 0, 1, 0], [0, 1, 0, 0, 1, 0, 1], [0, 0, 0, 1, 0, 1, 0]] edges = [[0, 0, 1, 2, 0, 0, 0], [0, 0, 2, 0, 0, 3, 0], [1, 2, 0, 1, 3, 0, 0], [2, 0, 1, 0, 0, 0, 1], [0, 0, 3, 0, 0, 2, 0], [0, 3, 0, 0, 2, 0, 1], [0, 0, 0, 1, 0, 1, 0]] # Find which vertex is to be visited next def to_be_visited(): global visited_and_distance v = -10 for index in range(num_of_vertices): if visited_and_distance[index][0] == 0 \ and (v < 0 or visited_and_distance[index][1] <= visited_and_distance[v][1]): v = index return v num_of_vertices = len(vertices[0]) visited_and_distance = [[0, 0]] for i in range(num_of_vertices-1): visited_and_distance.append([0, sys.maxsize]) for vertex in range(num_of_vertices): # Find next vertex to be visited to_visit = to_be_visited() for neighbor_index in range(num_of_vertices): # Updating new distances if vertices[to_visit][neighbor_index] == 1 and \ visited_and_distance[neighbor_index][0] == 0: new_distance = visited_and_distance[to_visit][1] \ + edges[to_visit][neighbor_index] if visited_and_distance[neighbor_index][1] > new_distance: visited_and_distance[neighbor_index][1] = new_distance visited_and_distance[to_visit][0] = 1 i = 0 # Printing the distance for distance in visited_and_distance: print("Distance of ", chr(ord('a') + i), " from source vertex: ", distance[1]) i = i + 1
Implementation in C++
// Dijkstra's Algorithm in C++ #include <iostream> #include <vector> #define INT_MAX 10000000 using namespace std; void DijkstrasTest(); int main() { DijkstrasTest(); return 0; } class Node; class Edge; void Dijkstras(); vector<Node*>* AdjacentRemainingNodes(Node* node); Node* ExtractSmallest(vector<Node*>& nodes); int Distance(Node* node1, Node* node2); bool Contains(vector<Node*>& nodes, Node* node); void PrintShortestRouteTo(Node* destination); vector<Node*> nodes; vector<Edge*> edges; class Node { public: Node(char id) : id(id), previous(NULL), distanceFromStart(INT_MAX) { nodes.push_back(this); } public: char id; Node* previous; int distanceFromStart; }; class Edge { public: Edge(Node* node1, Node* node2, int distance) : node1(node1), node2(node2), distance(distance) { edges.push_back(this); } bool Connects(Node* node1, Node* node2) { return ( (node1 == this->node1 && node2 == this->node2) || (node1 == this->node2 && node2 == this->node1)); } public: Node* node1; Node* node2; int distance; }; /////////////////// void DijkstrasTest() { Node* a = new Node('a'); Node* b = new Node('b'); Node* c = new Node('c'); Node* d = new Node('d'); Node* e = new Node('e'); Node* f = new Node('f'); Node* g = new Node('g'); Edge* e1 = new Edge(a, c, 1); Edge* e2 = new Edge(a, d, 2); Edge* e3 = new Edge(b, c, 2); Edge* e4 = new Edge(c, d, 1); Edge* e5 = new Edge(b, f, 3); Edge* e6 = new Edge(c, e, 3); Edge* e7 = new Edge(e, f, 2); Edge* e8 = new Edge(d, g, 1); Edge* e9 = new Edge(g, f, 1); a->distanceFromStart = 0; // set start node Dijkstras(); PrintShortestRouteTo(f); } /////////////////// void Dijkstras() { while (nodes.size() > 0) { Node* smallest = ExtractSmallest(nodes); vector<Node*>* adjacentNodes = AdjacentRemainingNodes(smallest); const int size = adjacentNodes->size(); for (int i = 0; i < size; ++i) { Node* adjacent = adjacentNodes->at(i); int distance = Distance(smallest, adjacent) + smallest->distanceFromStart; if (distance < adjacent->distanceFromStart) { adjacent->distanceFromStart = distance; adjacent->previous = smallest; } } delete adjacentNodes; } } // Find the node with the smallest distance, // remove it, and return it. Node* ExtractSmallest(vector<Node*>& nodes) { int size = nodes.size(); if (size == 0) return NULL; int smallestPosition = 0; Node* smallest = nodes.at(0); for (int i = 1; i < size; ++i) { Node* current = nodes.at(i); if (current->distanceFromStart < smallest->distanceFromStart) { smallest = current; smallestPosition = i; } } nodes.erase(nodes.begin() + smallestPosition); return smallest; } // Return all nodes adjacent to 'node' which are still // in the 'nodes' collection. vector<Node*>* AdjacentRemainingNodes(Node* node) { vector<Node*>* adjacentNodes = new vector<Node*>(); const int size = edges.size(); for (int i = 0; i < size; ++i) { Edge* edge = edges.at(i); Node* adjacent = NULL; if (edge->node1 == node) { adjacent = edge->node2; } else if (edge->node2 == node) { adjacent = edge->node1; } if (adjacent && Contains(nodes, adjacent)) { adjacentNodes->push_back(adjacent); } } return adjacentNodes; } // Return distance between two connected nodes int Distance(Node* node1, Node* node2) { const int size = edges.size(); for (int i = 0; i < size; ++i) { Edge* edge = edges.at(i); if (edge->Connects(node1, node2)) { return edge->distance; } } return -1; // should never happen } // Does the 'nodes' vector contain 'node' bool Contains(vector<Node*>& nodes, Node* node) { const int size = nodes.size(); for (int i = 0; i < size; ++i) { if (node == nodes.at(i)) { return true; } } return false; } /////////////////// void PrintShortestRouteTo(Node* destination) { Node* previous = destination; cout << "Distance from start: " << destination->distanceFromStart << endl; while (previous) { cout << previous->id << " "; previous = previous->previous; } cout << endl; } // these two not needed vector<Edge*>* AdjacentEdges(vector<Edge*>& Edges, Node* node); void RemoveEdge(vector<Edge*>& Edges, Edge* edge); vector<Edge*>* AdjacentEdges(vector<Edge*>& edges, Node* node) { vector<Edge*>* adjacentEdges = new vector<Edge*>(); const int size = edges.size(); for (int i = 0; i < size; ++i) { Edge* edge = edges.at(i); if (edge->node1 == node) { cout << "adjacent: " << edge->node2->id << endl; adjacentEdges->push_back(edge); } else if (edge->node2 == node) { cout << "adjacent: " << edge->node1->id << endl; adjacentEdges->push_back(edge); } } return adjacentEdges; } void RemoveEdge(vector<Edge*>& edges, Edge* edge) { vector<Edge*>::iterator it; for (it = edges.begin(); it < edges.end(); ++it) { if (*it == edge) { edges.erase(it); return; } } }
Time & Space Complexity Analysis
Time Complexity: O(E Log V)
where, E is the number of edges and V is the number of vertices.
Space Complexity: O(V)
Dijkstra's Algorithm Applications
1. To find the shortest path
2. In social networking applications
3. In a telephone network
4. To find the locations in the map
With this article at Logicmojo, you must have the complete idea of analyzing Dijkstra's algorithm.
Good Luck & Happy Learning!!
