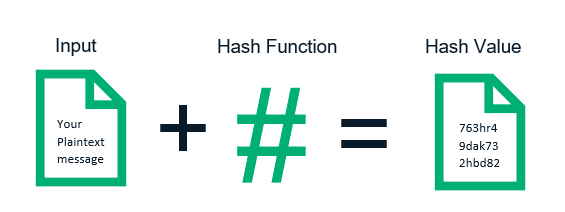
Hashing is the most important Data Struct that we use every day which is designed to use a special formula to encode the given value with a particular key for faster access of elements. the efficiency of hashing depends on the formula we used. Let's go into detail

What is a hash table?

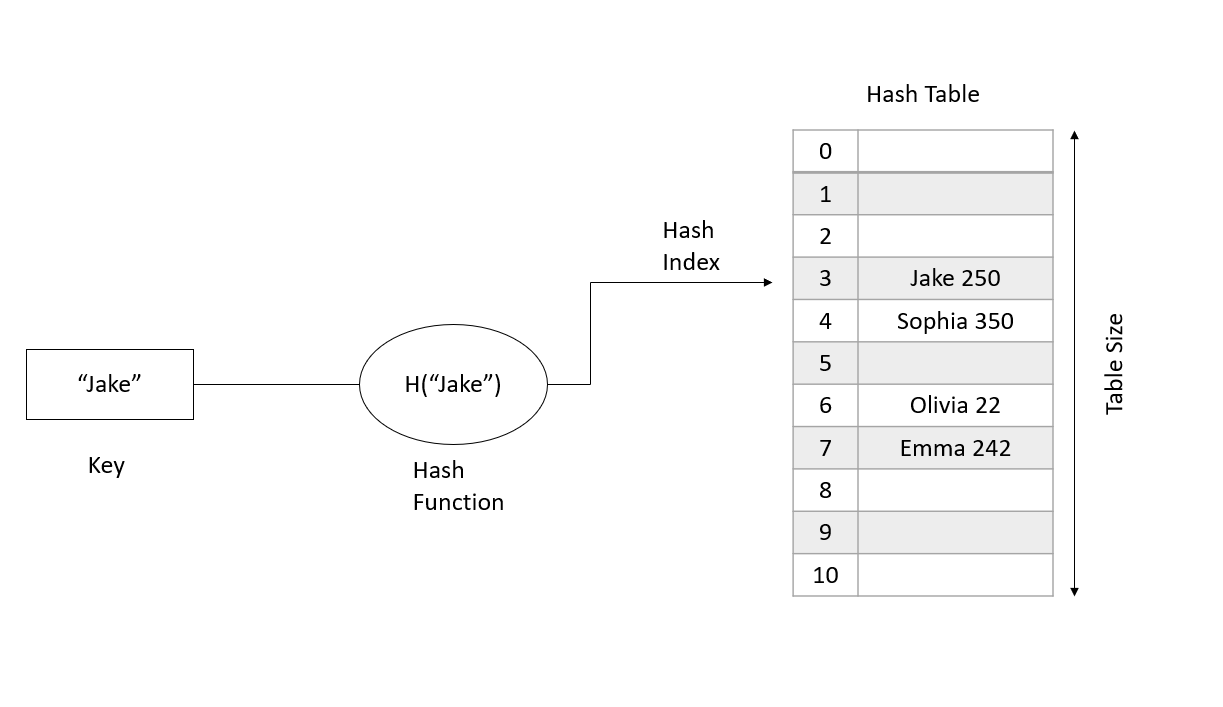
A hash table is a data structure that is used to store data. Initially it looks a lot like an array or a list but it separates itself from those by allowing for very fast data retrieval, no matter how much data there is.

A hash table accomplishes this by using a hash function. This is a function that maps the index of the hash table, to the value of the data that is stored. This means that in contrast to other data structures, the time complexity of finding elements is always equal to one.

When and why do we need HashTable??

Hash Table data structure is used when we have elements in key-value pairs and we want to search, insert, or delete any pair in average constant time. However, we should keep in mind that the elements are arranged in any irrelevant order in a hash table.

Key Components Required for Hashing:

Hash Function: This function converts a key into integer values which serve as the location(array index)where the key-value pair is stored corresponding to that key. A good hash function is one that is fast to compute and if using that hash function there are fewer chances of a collision.

Operation in hash function:

Insert - T[ h(key) ] = value;
It calculates the hash, uses it as the key and stores the value in hash table.

Delete - T[ h(key) ] = NULL;
It calculates the hash, resets the value stored in the hash table for that key.

Search - return T[ h(key) ];
It calculates the hash, finds and returns the value stored in the hash table for that key.

Hash Collision: When two or more inputs are mapped to the same keys as used in the hash table. Example: h(“John”) == h( “joe”)

A collision cannot be completely avoided but can be minimized using a ‘good’ hash function and a bigger table size. The chances of hash collision are less if the table size is a prime number.

How to choose a Hash Function

 • An efficient hash function should be built such that the index value of the added item is distributed equally across the table.
 • An effective collision resolution technique should be created to generate an alternate index for a key whose hash index corresponds to a previously inserted position in a hash table.

 • We must select a hash algorithm that is fast to calculate.

What makes up a good hash function?

 • Uses only the data being hashed
 • Is deterministic
 • Uniformly distributes data
 • Generates very different hash codes for similar data

Hash Collision

When the hash function generates the same index for multiple keys, there will be a conflict (what value to be stored in that index). This is called a hash collision.

We can resolve the hash collision using one of the following techniques.
Collision resolution by chaining
Open Addressing: Linear/Quadratic Probing and Double Hashing

Collisions and How to Handle Them

Two or more keys can generate same hash values sometimes. This is called a collision. A collision can be handled using various techniques.
Separate Chaining Technique

The idea is to make each cell of the hash table point to a linked list of records that have the same hash function values. It is simple but requires additional memory outside the table. In this technique, the worst case occurs when all the values are in the same index or linked list, making the search complexity linear (n=length of the linked list). This method should be used when we do not know how many keys will be there or how frequently the insert/delete operations will take place.

To maintain the O(1) time of insertions, we make the new value as head of the linked list of the particular index.

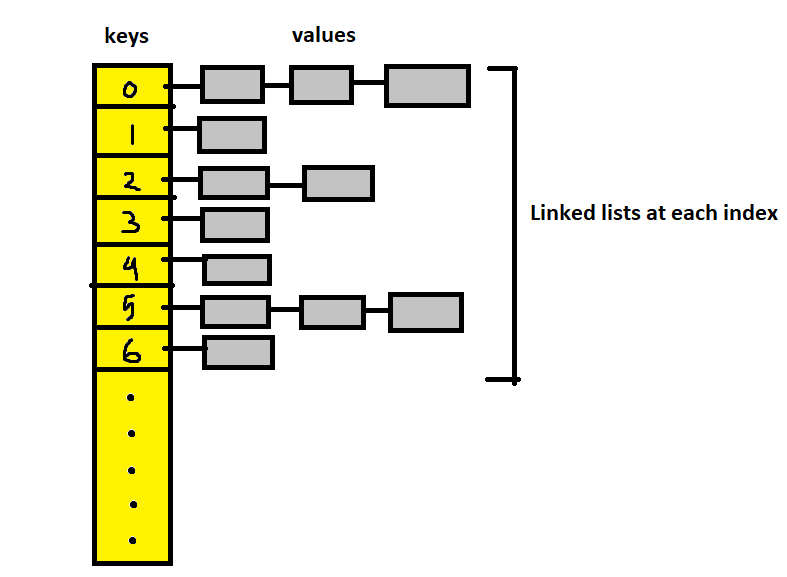
Below is the code of a generic hash table implementation with separate chaining technique, using an ArrayList of linked lists.

// this is the custom generic node class
public class HashNode<K,V> {
    
    K key;
    V value;
    HashNode<K,V> next;
    
    public HashNode(K key,V value){
        this.key = key;
        this.value = value;
    }
}

Open Addressing technique

In this method, the values are all stored in the hash table itself. If collision occurs, we look for availability in the next spot generated by an algorithm. The table size at all times should be greater than the number of keys. It is used when there is space restrictions, like in embedded processors. Point to note in delete operations, the deleted slot needs to be marked in some way so that during searching, we don’t stop probing at empty slots.

Types of Open Addressing:
Linear Probing: We linearly probe/look for next slot. If slot [hash(x)%size] is full, we try [hash(x)%size+1]. If that is full too, we try [hash(x)%size+2]…until an available space is found. Linear Probing has the best cache performance but downside includes primary and secondary clustering.
Quadratic Probing: We look for i²th iteration. If slot [hash(x)%size] is full, we try [(hash(x)+1*1)%size]. If that is also full, we try [(hash(x)+2*2)%size]…until an available space is found. Secondary clustering might arise here and there is no guarantee of finding a slot in this approach.
Double Hashing: We use a second hash function hash2(x) and look for i*hash2(x) slot. If slot [hash(x)%size] is full, we try [(hash(x)+1*hash2(x))%size]. If that is full too, we try [(hash(x)+2*hash2(x))%size]…until an available space is found. No primary or secondary clustering but lot more computation here.

Working of Hashtable in Python, C++

# Python program to demonstrate working of HashTable 

hashTable = [[],] * 10

def checkPrime(n):
    if n == 1 or n == 0:
        return 0

    for i in range(2, n//2):
        if n % i == 0:
            return 0

    return 1


def getPrime(n):
    if n % 2 == 0:
        n = n + 1

    while not checkPrime(n):
        n += 2

    return n


def hashFunction(key):
    capacity = getPrime(10)
    return key % capacity


def insertData(key, data):
    index = hashFunction(key)
    hashTable[index] = [key, data]

def removeData(key):
    index = hashFunction(key)
    hashTable[index] = 0

insertData(123, "apple")
insertData(432, "mango")
insertData(213, "banana")
insertData(654, "guava")

print(hashTable)

removeData(123)

print(hashTable)

// Implementing hash table in C++

#include <iostream>
#include <list>
using namespace std;

class HashTable
{
  int capacity;
  list<int> *table;

public:
  HashTable(int V);
  void insertItem(int key, int data);
  void deleteItem(int key);

  int checkPrime(int n)
  {
  int i;
  if (n == 1 || n == 0)
  {
    return 0;
  }
  for (i = 2; i < n / 2; i++)
  {
    if (n % i == 0)
    {
    return 0;
    }
  }
  return 1;
  }
  int getPrime(int n)
  {
  if (n % 2 == 0)
  {
    n++;
  }
  while (!checkPrime(n))
  {
    n += 2;
  }
  return n;
  }

  int hashFunction(int key)
  {
  return (key % capacity);
  }
  void displayHash();
};
HashTable::HashTable(int c)
{
  int size = getPrime(c);
  this->capacity = size;
  table = new list<int>[capacity];
}
void HashTable::insertItem(int key, int data)
{
  int index = hashFunction(key);
  table[index].push_back(data);
}

void HashTable::deleteItem(int key)
{
  int index = hashFunction(key);

  list<int>::iterator i;
  for (i = table[index].begin();
   i != table[index].end(); i++)
  {
  if (*i == key)
    break;
  }

  if (i != table[index].end())
  table[index].erase(i);
}

void HashTable::displayHash()
{
  for (int i = 0; i < capacity; i++)
  {
  cout << "table[" << i << "]";
  for (auto x : table[i])
    cout << " --> " << x;
  cout << endl;
  }
}

int main()
{
  int key[] = {231, 321, 212, 321, 433, 262};
  int data[] = {123, 432, 523, 43, 423, 111};
  int size = sizeof(key) / sizeof(key[0]);

  HashTable h(size);

  for (int i = 0; i < size; i++)
  h.insertItem(key[i], data[i]);

  h.deleteItem(12);
  h.displayHash();
}

Applications of Hash Table

Hash tables are implemented where< constant time lookup and insertion is required
cryptographic applications
indexing data is required

With this article at Logicmojo, you must have the complete idea of analyzing Hash Data Structure.

Good Luck & Happy Learning!!