 Logicmojo - Updated Sept 18, 2021
Logicmojo - Updated Sept 18, 2021
When talking about Computer Science, sorting algorithms are one of the most essential part of the theme. These algorithms can be different from each other owing to its efficiency and the time that is taken to finish the task. Despite the fact that there are a myriad of sorting algorithms, today we’ ll learn the algorithm with the time complexity of O(n lg(n)) which is averagely so fast.
A heap sort is a sorting algorithm based on the binary heap data structure. The idea behind a heap sort is to find the highest value and place it at the end, repeating the process until everything is sorted.
In order to fully understand how a heap sort works, we first have to understand a binary heap, and subsequently, a binary tree. A binary tree is a tree data structure where each element has at most 2 children. A binary heap is simply a complete binary tree, in which each level of the tree (except, perhaps, the last level) is completely filled and all nodes are stored starting from the left to right. A binary heap also takes into account how the values are stored. Either the value of the parent node is always greater than the value of its children (called a max heap), or vice versa, where the value of the parent is smaller than that of its children (called a min heap). A heap sort will utilize a max heap to sort its elements.
WHAT IS HEAP?
Heap is a tree-based data structure in which all the nodes of the tree are in a specific order. Heap is always a complete binary tree. While converting a Heap to an array we must keep in mind the following:
The root element of the heap should be at index 0 in the array.
For the node at index i:
At index (i-1)/2 is the parent node
At index (2*i)+1 is the left child node
At index (2*i)+2 is the right child node
Heaps are of the following two types:
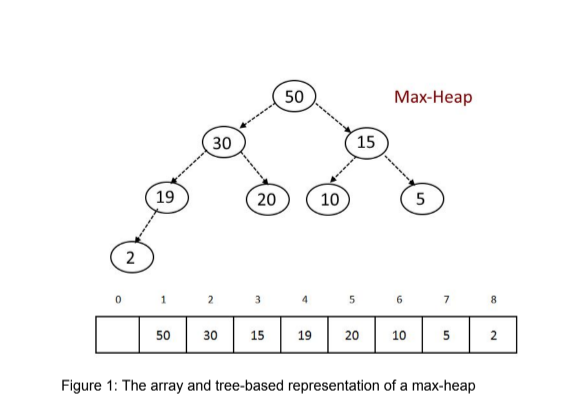
MAX HEAP
In this type of heap, the value of the parent node is always larger than the child nodes. Hence, the root node is occupied by the largest value in the whole heap.
To understand how to convert a heap into a max heap, let’s see the example below.
Complexity for max heap in O(logN).
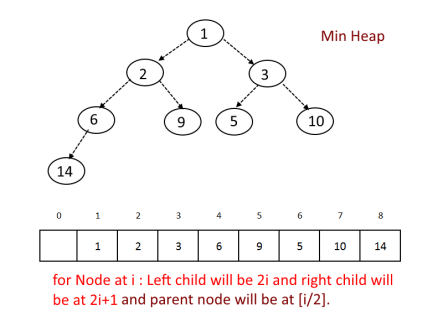
MIN HEAP
In this type of heap, the value of the parent will always be less than both of the children. Hence, the least value in the whole heap is at the root of the heap.
To understand this better let's see this quick example.
HEAP SORT ALGORITHM
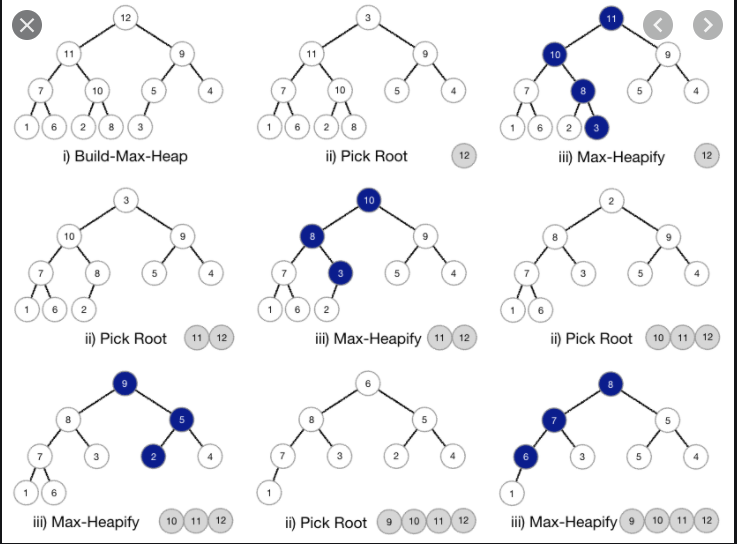
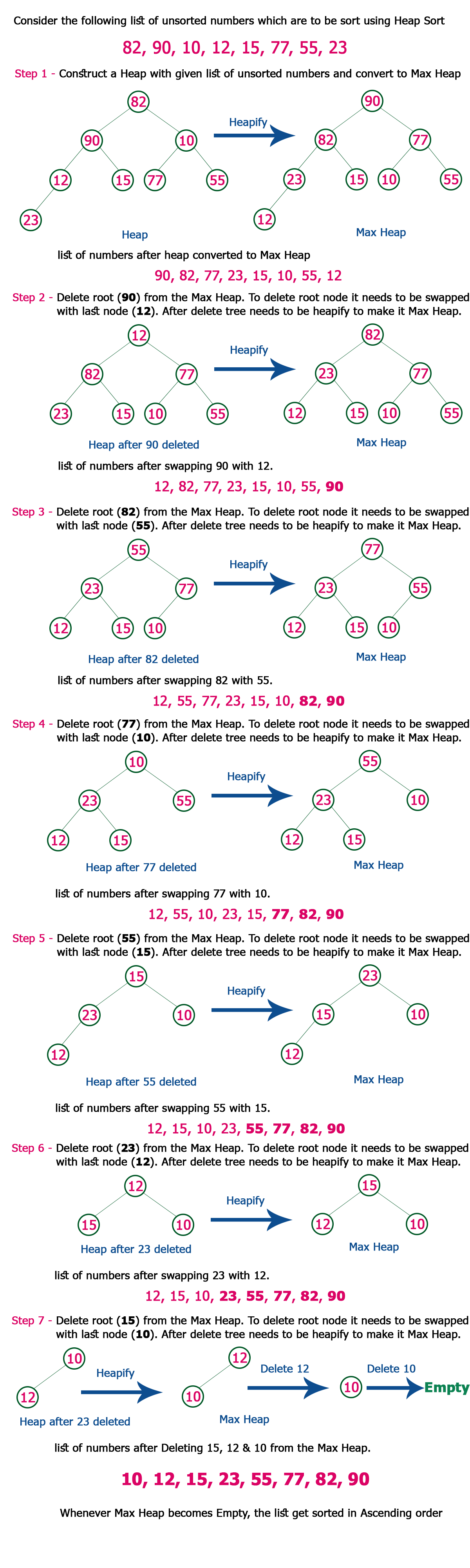
There are various kinds of sorting methods used in sorting different kinds of data structures. One of the popular and efficient sorting methods in computer science is Heap Sort which requires the knowledge of arrays and trees/heap. Now let us see how heap sort works and what steps we have to use.
1. From the elements of the given array, we have to make a max heap. We can start heapifying each sub-tree from the bottom up and end up with a max-heap after the function is applied to all the elements including the root element.
2. Remove the root element and put it at the end of the array (nth position) Put the last item of the tree (heap) at the vacant place.
3. Reduce the size of the heap by 1.
4. Heapify the root element again so that we have the highest element at root.
5. Keep repeating this process again and again until all the items of the list are sorted in the array successfully.
HEAP SORT APPLICATION
Systems concerned with security and embedded systems such as Linux Kernel use Heap Sort because of the O(nlog n) upper bound on Heapsort's running time and constant o(1) upper bound on its auxiliary storage.
Heap can be efficiently used if we want to extract the smallest (or largest) from the list of items without the overhead of keeping the remaining items in the sorted order. For e.g Priority Queues.
Implementation in Python
# Heap Sort in python def heapify(arr, n, i): # Find largest among root and children largest = i l = 2 * i + 1 r = 2 * i + 2 if l < n and arr[i] < arr[l]: largest = l if r < n and arr[largest] < arr[r]: largest = r # If root is not largest, swap with largest and continue heapifying if largest != i: arr[i], arr[largest] = arr[largest], arr[i] heapify(arr, n, largest) def heapSort(arr): n = len(arr) # Build max heap for i in range(n//2, -1, -1): heapify(arr, n, i) for i in range(n-1, 0, -1): # Swap arr[i], arr[0] = arr[0], arr[i] # Heapify root element heapify(arr, i, 0) arr = [1, 12, 9, 5, 6, 10] heapSort(arr) n = len(arr) print("Sorted array is") for i in range(n): print("%d " % arr[i], end='')
Implementation in C++
// Heap Sort in C++ #include <iostream> using namespace std; void heapify(int arr[], int n, int i) { // Find largest among root, left child and right child int largest = i; int left = 2 * i + 1; int right = 2 * i + 2; if (left < n && arr[left] > arr[largest]) largest = left; if (right < n && arr[right] > arr[largest]) largest = right; // Swap and continue heapifying if root is not largest if (largest != i) { swap(arr[i], arr[largest]); heapify(arr, n, largest); } } // main function to do heap sort void heapSort(int arr[], int n) { // Build max heap for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // Heap sort for (int i = n - 1; i >= 0; i--) { swap(arr[0], arr[i]); // Heapify root element to get highest element at root again heapify(arr, i, 0); } } // Print an array void printArray(int arr[], int n) { for (int i = 0; i < n; ++i) cout << arr[i] << " "; cout << "\n"; } // Driver code int main() { int arr[] = {1, 12, 9, 5, 6, 10}; int n = sizeof(arr) / sizeof(arr[0]); heapSort(arr, n); cout << "Sorted array is \n"; printArray(arr, n); }
Time & Space Complexity Analysis
Time complexity of heapify is O(Logn). Time complexity of createAndBuildHeap() is O(n) and the overall time complexity of Heap Sort is O(nLogn).
| Time complexity | |
|---|---|
| Best | O(nlogn) |
| Worst | O(nlogn) |
| Average | O(nlogn) |
| Stability | No |
Space Complexity:O(1)
With this article at Logicmojo, you must have the complete idea of analyzing Heap Sort algorithm.
Good Luck & Happy Learning!!
