Intersection of Two Linked Lists

Back to home

𝑻𝒂𝒃𝒍𝒆 𝒐𝒇 𝑪𝒐𝒏𝒕𝒆𝒏𝒕

Problem Statement: Intersection of Two Linked Lists
Naive Approach
Efficient-Length Difference
Efficient-Two Pointer

Logicmojo - Updated Aug 28, 2021

Problem Statement: Intersection of Two Linked Lists

Given the heads of two singly linked-lists headA and headB, return the node at which the two lists intersect. If the two linked lists have no intersection at all, return null.

Example

listA = [4,1,8,4,5], listB = [5,6,1,8,4,5]

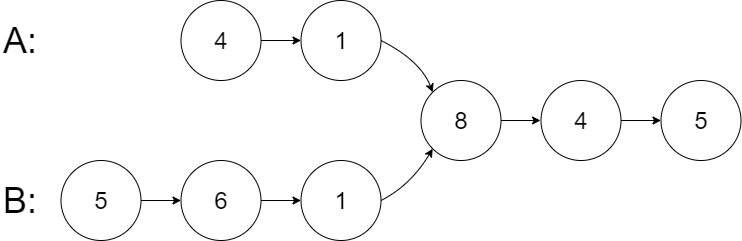
Output: Intersected at '8'

We have presented three approaches to solve the problem:

• Naive Approach
• Efficient - Length Difference
• Efficient - Two Pointer

Naive Approach

For every node in the List A, traverse the entire List B. Return the node if the nodes from List A and List B are equal. Else return null. Time Complexity will be O(M*N), i.e not efficient so we need to optimise it.

Approach 2: Efficient - Length Difference

Find out the two linked lists lengths. Whichever list is longer, traverse the length difference of that list from the head so that both pointers are at the same position to the list ends. Then traverse both lists in parallel then you will automatically reach the intersection point.

C++ Implementation:

class Solution {
public:
	ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) {
		int n = 0;
		int m = 0;
		ListNode* ptr1 = headA;
		ListNode* ptr2 = headB;
		while(ptr1 != NULL){
			n++;
			ptr1 = ptr1 -> next;
		}
		while(ptr2 != NULL){
			m++;
			ptr2 = ptr2 -> next;
		}
		int t = abs(n - m);
		if(n > m){
			while(t){
				headA = headA -> next;
				t--;
			}
		}
		else{
			while(t){
				headB = headB -> next;
				t--;
			}
		}
		while(headA != NULL and headB != NULL){
			if(headA == headB){
				return headA;
			}
			headA = headA -> next;
			headB = headB -> next;
		}
		return NULL;
	}
};

Python Implementation:

# A Linked List Node-->
class Node:
    def __init__(self, data, next = None):
        self.data = data
        self.next = next
 
 
# Utility function to find the total number of nodes in a linked list
def size(head):
    nodes = 0
    while head:
        nodes += 1
        head = head.next
    return nodes
 
 
# Function to find the intersection point of two linked lists.
# Assume that the first list contains `k` nodes more than the second list
def findIntersection(first, second, k):
 
    # advance the bigger list by `k` nodes
    i = 0
    while i < k and first:
        first = first.next
        i += 1
 
    # simultaneously move both lists at the same speed until they meet
    while first and second:
        # if both lists meet any node, then that node is the intersection point
        if first == second:
            return first
        # advance both lists by one node
        first = first.next
        second = second.next
 
    # return None if both lists don't meet
    return None
 
 
# Function to find the intersection point of two linked lists
def findIntersectionPt(first, second):
 
    # get the difference in the number of nodes in both lists
    diff = size(first) - size(second)
 
    # if the first list has a smaller number of nodes, exchange both lists
    if diff < 0:
        node = first
        first = second
        second = node
 
    # find and return the intersection node
    return findIntersection(first, second, abs(diff))
 
 
if __name__ == '__main__':
 
    # construct the first linked list (1 —> 2 —> 3 —> 4 —> 5 —> None)
    first = None
    for i in reversed(range(1, 6)):
        first = Node(i, first)
 
    # construct the second linked list (1 —> 2 —> 3 —> None)
    second = None
    for i in reversed(range(1, 4)):
        second = Node(i, second)
 
    # link tail of the second list to the fourth node of the first list
    second.next.next.next = first.next.next.next
 
    addr = findIntersectionPt(first, second)
    if addr:
        print('The intersection point is', addr.data)
    else:
        print('The lists do not intersect.')

Time Complexity: O(M + N) where M and N are number of nodes in ListA and ListB

Space Complexity:O(1)

Approach 3: Two Pointer

We can use two iterations to do that. In the first iteration, we will reset the pointer of one linkedlist to the head of another linkedlist after it reaches the tail node. In the second iteration, we will move two pointers until they points to the same node. Our operations in first iteration will help us counteract the difference. So if two linkedlist intersects, the meeting point in second iteration must be the intersection point. If the two linked lists have no intersection at all, then the meeting pointer in second iteration must be the tail node of both lists, which is null

C++ Implementation:

ListNode *getIntersectionNode(ListNode *headA, ListNode *headB) 
{
    ListNode *p1 = headA;
    ListNode *p2 = headB;
        
    if (p1 == NULL || p2 == NULL) return NULL;

    while (p1 != NULL && p2 != NULL && p1 != p2) {
        p1 = p1->next;
        p2 = p2->next;

        //
        // Any time they collide or reach end together without colliding 
        // then return any one of the pointers.
        //
        if (p1 == p2) return p1;

        //
        // If one of them reaches the end earlier then reuse it 
        // by moving it to the beginning of other list.
        // Once both of them go through reassigning, 
        // they will be equidistant from the collision point.
        //
        if (p1 == NULL) p1 = headB;
        if (p2 == NULL) p2 = headA;
    }
        
    return p1;
}

Python Implementation:

class Solution:
    def getIntersectionNode(self, headA, headB):
        if headA is None or headB is None:
            return None

        pa = headA // 2 pointers
        pb = headB

        while pa is not pb:
            // if either pointer hits the end, switch head and continue the second traversal, 
            // if not hit the end, just move on to next
            pa = headB if pa is None else pa.next
            pb = headA if pb is None else pb.next

        return pa // only 2 ways to get out of the loop, they meet or the both hit the end=None

Time Complexity: O(N) N are number of nodes in Linked List

Space Complexity:O(1)

With this article at Logicmojo, you must have the complete idea of solving Intersection of Two Linked Lists problem.