Knight's Journey On A Chessboard

Back to home

𝑻𝒂𝒃𝒍𝒆 𝒐𝒇 𝑪𝒐𝒏𝒕𝒆𝒏𝒕

Problem Statement: Knight's Journey On A Chessboard
Approach: Using BFS

Logicmojo - Updated Aug 28, 2021

Problem Statement: Knight's Journey On A Chessboard

You have a chessboard of size n*n. A knight sits on the board at a position start(x, y). The knight wants to go to another cell end(x, y). Find the minimum number of moves required to go from the start position to the end position. If this is not possible, return -1.

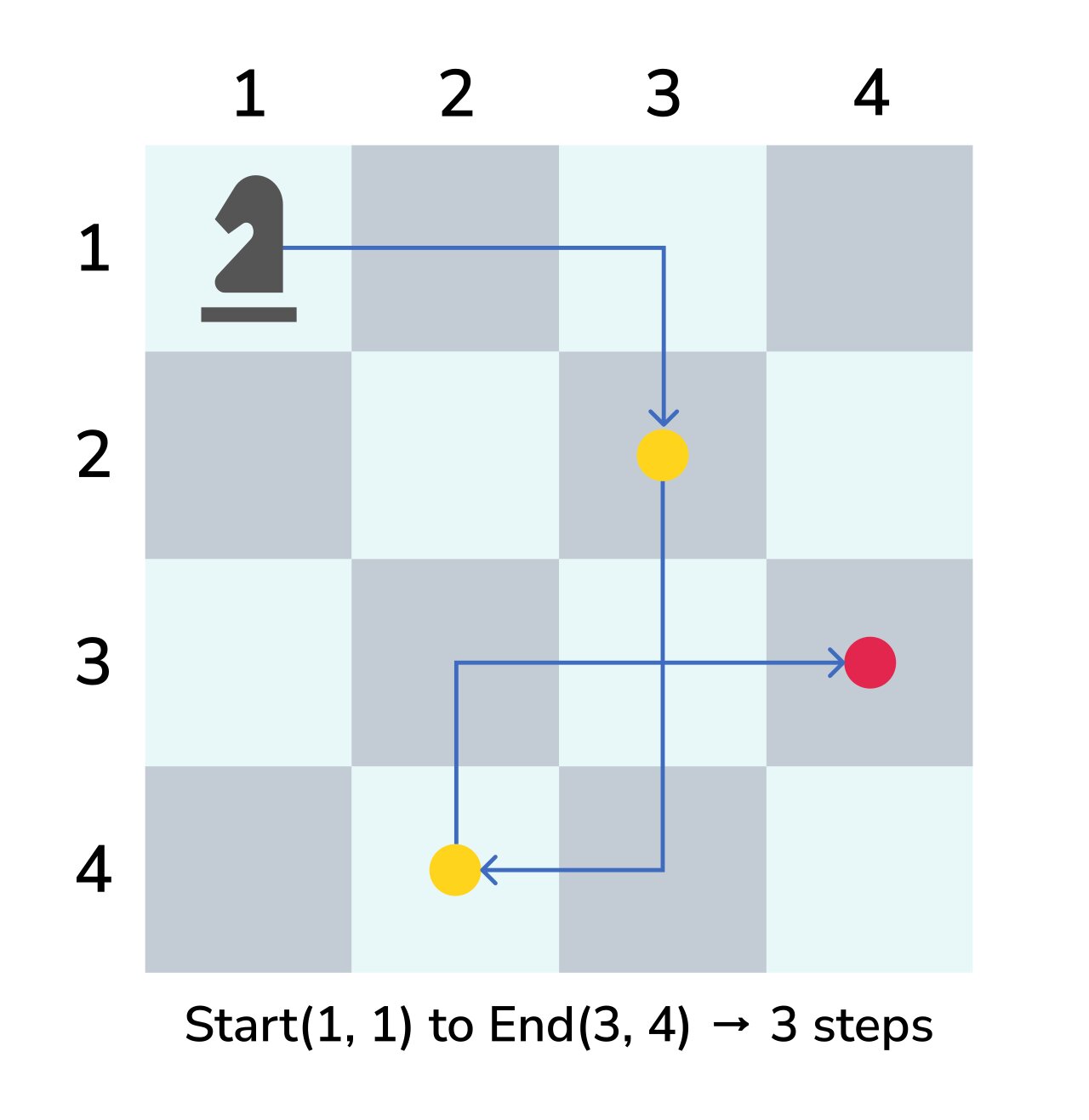
Example: N = 30, knightpos = [1, 1], targetpos = [30, 30]

Output: 20

Approach: Using BFS

This problem can be seen as shortest path in unweighted graph. Therefore we use BFS to solve this problem. We try all 8 possible positions where a Knight can reach from its position. If reachable position is not already visited and is inside the board, we push this state into queue with distance 1 more than its parent state. Finally we return distance of target position, when it gets pop out from queue.

C++ Implementation:

#include <bits/stdc++.h>
using namespace std;

// structure for storing a cell's data
struct cell {
	int x, y;
	int dis;
	cell() {}
	cell(int x, int y, int dis)
		: x(x), y(y), dis(dis)
	{
	}
};


bool isInside(int x, int y, int N)
{
	if (x >= 1 && x <= N && y >= 1 && y <= N)
		return true;
	return false;
}


int minStepToReachTarget(
	int knightPos[], int targetPos[],
	int N)
{
	// x and y direction, where a knight can move
	int dx[] = { -2, -1, 1, 2, -2, -1, 1, 2 };
	int dy[] = { -1, -2, -2, -1, 1, 2, 2, 1 };

	
	q.push(cell(knightPos[0], knightPos[1], 0));

	cell t;
	int x, y;
	bool visit[N + 1][N + 1];

	
	for (int i = 1; i <= N; i++)
		for (int j = 1; j <= N; j++)
			visit[i][j] = false;

	
	visit[knightPos[0]][knightPos[1]] = true;

	
	while (!q.empty()) {
		t = q.front();
		q.pop();

		
		if (t.x == targetPos[0] && t.y == targetPos[1])
			return t.dis;

		// loop for all reachable states
		for (int i = 0; i < 8; i++) {
			x = t.x + dx[i];
			y = t.y + dy[i];

			
			if (isInside(x, y, N) && !visit[x][y]) {
				visit[x][y] = true;
				q.push(cell(x, y, t.dis + 1));
			}
		}
	}
}

// Driver code to test above methods
int main()
{
	int N = 30;
	int knightPos[] = { 1, 1 };
	int targetPos[] = { 30, 30 };
	cout << minStepToReachTarget(knightPos, targetPos, N);
	return 0;
}

Python Implementation:

from collections import deque
def mini_step(knightpos, targetpos):
    queue = deque([[knightpos[0], knightpos[1], 0]])
    seen = set()
    seen.add((knightpos[0], knightpos[1]))
    while queue:
        i, j, dist = queue.popleft()
        if i == targetpos[0] and j == targetpos[1]: return dist
        for k in range(8):
            x, y = i + X[k], j + Y[k]
            if 1 <= x <= n and 1 <= y <= n and (x, y) not in seen:
                queue.append((x, y, dist + 1))
                seen.add((x, y))
                
knightpos = [1,1]
targetpos = [30,30]
X = [2, 2, -2, -2, 1, 1, -1, -1]
Y = [1, -1, 1, -1, 2, -2, 2, -2]
n = 30
print(mini_step(knightpos, targetpos))

Time Complexity: O(N²) At worst case, all the cells will be visited so time complexity is O(N²).

Space Complexity: O(N²). The nodes are stored in queue. So the space Complexity is O(N²).

With this article at Logicmojo, you must have the complete idea of solving Knight's Journey On A Chessboard problem.