Greedy algorithms are generally used for optimization problems. For this suppose we have a graph and edges of a graph that may be used to build a path. Minimum spanning tree is subset of the edges of a connected graph, edge weighted undirected graph that connects all the vertices together, without any cycles and with the minimum possible total edge weight and that’s call minimum spanning tree. Kruskal’s algorithm is one of them, we are using this algorithm for minimum spanning tree.

What is Minimum Spanning Tree?

• It is a tree (i.e., it is acyclic).
• It covers all the vertices V – contains |V| — 1 edges.
• The total cost associated with tree edges is the minimum among all possible spanning trees.
• not necessarily unique.

Implementation of Krushkal’s Algorithm

• The algorithm first sorts all the edges in nondecreasing order of their weight.

• Edge with minimum weight is selected and its feasibility is tested.

• If inclusion of the edge to a partial solution does not form the cycle, then the edge is feasible and added to the partial solution.

• If is not feasible then skip it and check for the next edge. The process is repeated until all edges are scanned.

• Let, list unvisited edges UE = {e1, e2, e3, . . . , em}, be the edges sorted by increasing order of their weight.

• Select minimum weight edge emin from input graph G, which is not already added.

• If the addition of edge emin to a partial solution does not form a cycle, add it. Otherwise look for next minimum weight edge until we get the feasible edge. Remove checked edges from E.

• Go to step 1 and repeat the procedure until all edges in E are scanned.

Krushkal’s Algorithm Example

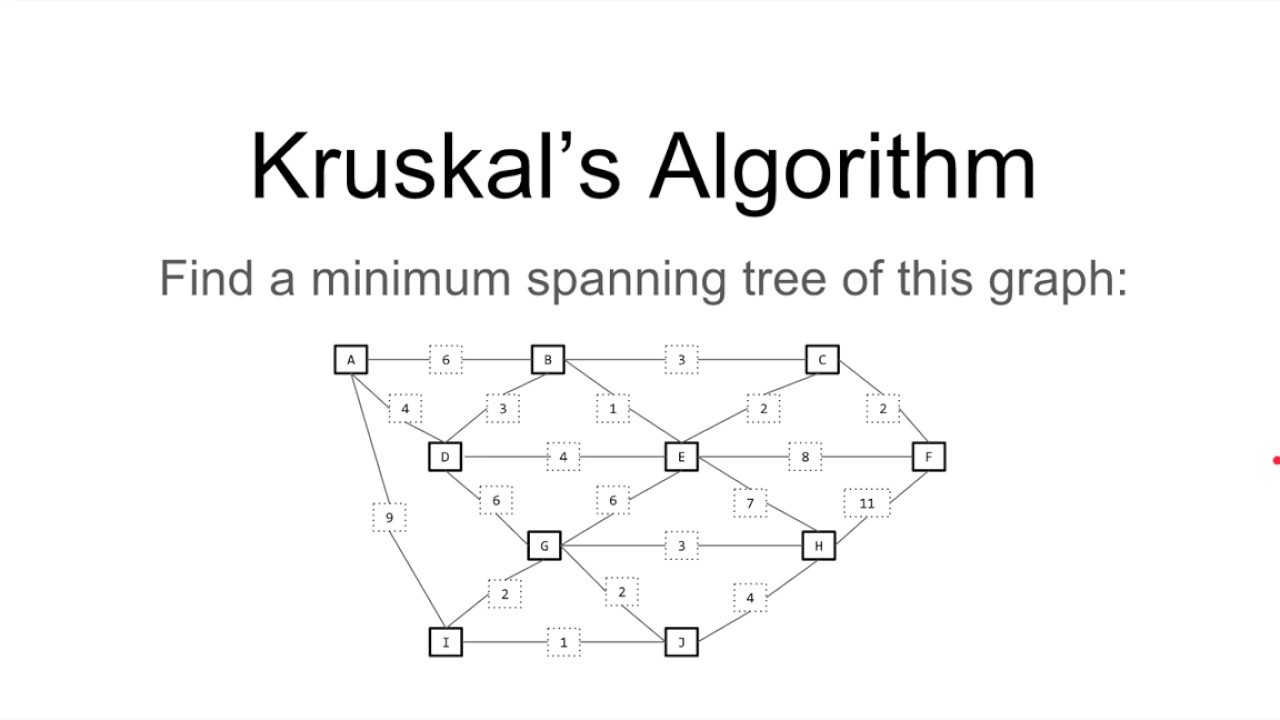
Example: Find the cost of Minimal Spanning Tree of the given graph by using Kruskal’s Algorithm

Let’s See an Example to understand Kruskal’s algorithm

Step 1 – Remove all loops and Parallel Edges

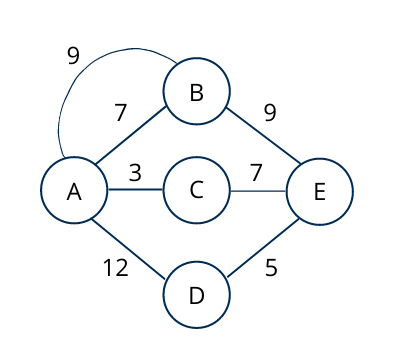
After removing parallel edge from the graph, graph will look like below.

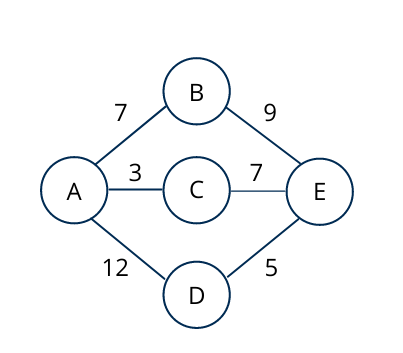
Step 2 – Sort all the edges in non-decreasing order of their weight
AC – 3, DE – 5, AB – 7, BE – 9, CE – 7, AD – 12

Step 3 – Pick the least weightage edge and include this edge

We will add edges to the graph beginning from the one which has the least weight. As well as also we will keep checking this edge should not form any cycle. In cycle will create by adding one edge or any other property that violates the spanning-tree property then we will not include the edge in the graph.

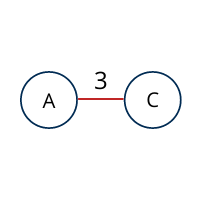
The least cost is 3 and the edges involved is AC. We add them. Adding them does not violate spanning-tree properties, so we continue to our next edge selection.

Next we will select Edge DE which have least weight 5 and not violating spanning tree properties.

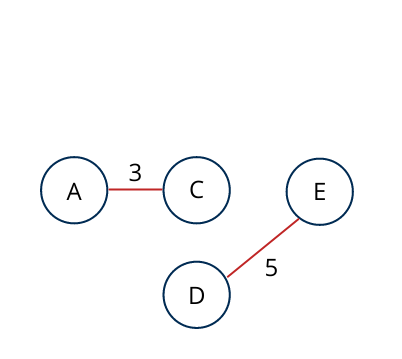
Next we will select Edge AB which have least weight 7 and not violating spanning tree properties.

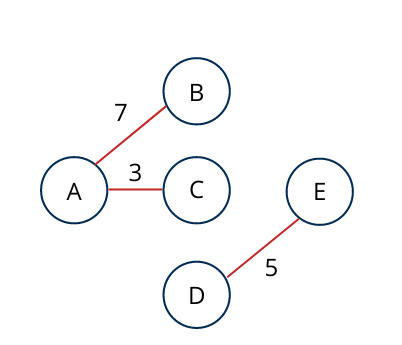
Next we will select Edge CE which have least weight 7 and not violating spanning tree properties.

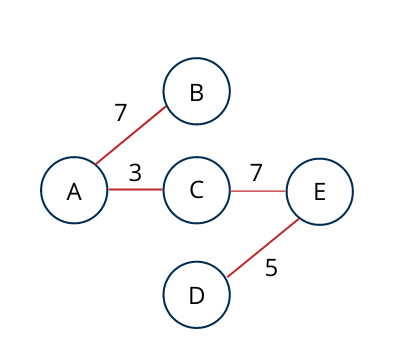
So Create Minimum spanning tree using Kruskal’s algorithm will look like above.

Implementation in Python

# Kruskal's algorithm in Python


class Graph:
    def __init__(self, vertices):
        self.V = vertices
        self.graph = []

    def add_edge(self, u, v, w):
        self.graph.append([u, v, w])

    # Search function

    def find(self, parent, i):
        if parent[i] == i:
            return i
        return self.find(parent, parent[i])

    def apply_union(self, parent, rank, x, y):
        xroot = self.find(parent, x)
        yroot = self.find(parent, y)
        if rank[xroot] < rank[yroot]:
            parent[xroot] = yroot
        elif rank[xroot] > rank[yroot]:
            parent[yroot] = xroot
        else:
            parent[yroot] = xroot
            rank[xroot] += 1

    #  Applying Kruskal algorithm
    def kruskal_algo(self):
        result = []
        i, e = 0, 0
        self.graph = sorted(self.graph, key=lambda item: item[2])
        parent = []
        rank = []
        for node in range(self.V):
            parent.append(node)
            rank.append(0)
        while e < self.V - 1:
            u, v, w = self.graph[i]
            i = i + 1
            x = self.find(parent, u)
            y = self.find(parent, v)
            if x != y:
                e = e + 1
                result.append([u, v, w])
                self.apply_union(parent, rank, x, y)
        for u, v, weight in result:
            print("%d - %d: %d" % (u, v, weight))


g = Graph(6)
g.add_edge(0, 1, 4)
g.add_edge(0, 2, 4)
g.add_edge(1, 2, 2)
g.add_edge(1, 0, 4)
g.add_edge(2, 0, 4)
g.add_edge(2, 1, 2)
g.add_edge(2, 3, 3)
g.add_edge(2, 5, 2)
g.add_edge(2, 4, 4)
g.add_edge(3, 2, 3)
g.add_edge(3, 4, 3)
g.add_edge(4, 2, 4)
g.add_edge(4, 3, 3)
g.add_edge(5, 2, 2)
g.add_edge(5, 4, 3)
g.kruskal_algo()

Implementation in C++

// Kruskal's algorithm in C++

#include <algorithm>
#include <iostream>
#include <vector>
using namespace std;

#define edge pair<int, int>

class Graph {
   private:
  vector<pair<int, edge> > G;  // graph
  vector<pair<int, edge> > T;  // mst
  int *parent;
  int V;  // number of vertices/nodes in graph
   public:
  Graph(int V);
  void AddWeightedEdge(int u, int v, int w);
  int find_set(int i);
  void union_set(int u, int v);
  void kruskal();
  void print();
};
Graph::Graph(int V) {
  parent = new int[V];

  //i 0 1 2 3 4 5
  //parent[i] 0 1 2 3 4 5
  for (int i = 0; i < V; i++)
    parent[i] = i;

  G.clear();
  T.clear();
}
void Graph::AddWeightedEdge(int u, int v, int w) {
  G.push_back(make_pair(w, edge(u, v)));
}
int Graph::find_set(int i) {
  // If i is the parent of itself
  if (i == parent[i])
    return i;
  else
    // Else if i is not the parent of itself
    // Then i is not the representative of his set,
    // so we recursively call Find on its parent
    return find_set(parent[i]);
}

void Graph::union_set(int u, int v) {
  parent[u] = parent[v];
}
void Graph::kruskal() {
  int i, uRep, vRep;
  sort(G.begin(), G.end());  // increasing weight
  for (i = 0; i < G.size(); i++) {
    uRep = find_set(G[i].second.first);
    vRep = find_set(G[i].second.second);
    if (uRep != vRep) {
      T.push_back(G[i]);  // add to tree
      union_set(uRep, vRep);
    }
  }
}
void Graph::print() {
  cout << "Edge :"
     << " Weight" << endl;
  for (int i = 0; i < T.size(); i++) {
    cout << T[i].second.first << " - " << T[i].second.second << " : "
       << T[i].first;
    cout << endl;
  }
}
int main() {
  Graph g(6);
  g.AddWeightedEdge(0, 1, 4);
  g.AddWeightedEdge(0, 2, 4);
  g.AddWeightedEdge(1, 2, 2);
  g.AddWeightedEdge(1, 0, 4);
  g.AddWeightedEdge(2, 0, 4);
  g.AddWeightedEdge(2, 1, 2);
  g.AddWeightedEdge(2, 3, 3);
  g.AddWeightedEdge(2, 5, 2);
  g.AddWeightedEdge(2, 4, 4);
  g.AddWeightedEdge(3, 2, 3);
  g.AddWeightedEdge(3, 4, 3);
  g.AddWeightedEdge(4, 2, 4);
  g.AddWeightedEdge(4, 3, 3);
  g.AddWeightedEdge(5, 2, 2);
  g.AddWeightedEdge(5, 4, 3);
  g.kruskal();
  g.print();
  return 0;
}

Time & Space Complexity Analysis

Time Complexity : O(ElogE) or O(ElogV)
Sorting of edges takes O(ELogE) time.
After sorting, we iterate through all edges and apply find-union algorithm.
The find and union operations can take at most O(LogV) time.
So overall complexity is O(ELogE + ELogV) time.
The value of E can be at most O(V2), so O(LogV) is O(LogE) the same.
Therefore, the overall time complexity is O(ElogE) or O(ElogV)

With this article at Logicmojo, you must have the complete idea of analyzing Krushkal's Algorithm.

Good Luck & Happy Learning!!