Kadane's Algorithm

Problem Statement: Largest Contiguous Sum

Kadane's Algorithm: Given an integer array arr, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum and print the subarray.

Example 1:
Input: arr = [-2,1,-3,4,-1,2,1,-5,4]
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.
Examples 2:
Input: arr = [1]
Output: 1
Explanation: Array has only one element and which is giving positive sum of 1.

We have presented two approaches to find the two elements:

Naive Approach

The array will have n numbers a₀ a₁...a_n An obvious solution runs in O(n³) time and it just iterates over all O(n²)slices and for each of them it calculates their sum. Of course it can be speeded-up to O(n²) by reusing the calculations, as below C++ implementation:

PseudoCode

Optimal Solution: Kadane’s Algorithm

What is Kadane’s Algorithm?

Kadane’s algorithm is one of the famous approaches to solve the problem using dynamic programming. As we all know, the maximum subarray problem is one of the famous problems in the field of dynamic programming. You must be thinking that the problem seems to be easy and the result of the problem will be the sum of all elements in an array. But this is not correct. There will be negative integer elements in the array that can decrease the sum of the entire array. Therefore, to solve this problem, we will use the kadane’s algorithm.

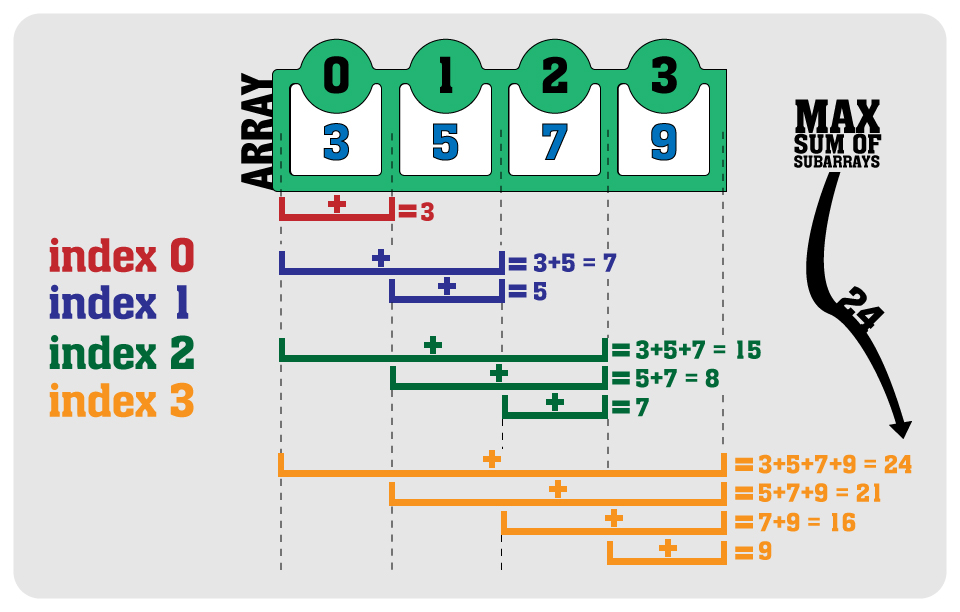
Here the algorithm will find the continuous subarray in the 1D integer array which has the largest sum possible. The first approach for everyone after understanding the problem statement will be applying the brute-force approach and solving the problem. But by doing so, the time complexity of the solution will be O(n2) which is not very good. Therefore, we will apply the kadane’s algorithm which solves the problem by traversing over the whole array using two variables to track the sum so far and maximum total. The most important thing to pay attention to while using this algorithm is the condition using which we will update both variables.

Algorithm for Maximum Subarray Sum:

1. Initializing max_till_now = 0

2. Initializing max_ending = 0

3. Repeat steps 4 to 6 for every element in the array

4. Set max_ending = max_ending + a[i]

5. if (max_ending < 0) then set max_ending = 0

6. if (max_till_now < max_ending) then set max_till_now = max_ending

7. return max_till_now

#include<bits/stdc++.h>

using namespace std;
int maxSubArray(vector < int > & nums, vector < int > & subarray) {
  int msf = nums[0], meh = 0;
  int s = 0;
  for (int i = 0; i < nums.size(); i++) {
    meh += nums[i];
    if (meh > msf) {
      subarray.clear();
      msf = meh;
      subarray.push_back(s);
      subarray.push_back(i);

    }
    if (meh < 0) {
      meh = 0;
      s = i + 1;

    }
  }

  return msf;
}

int main() {
  vector<int> arr{-2,1,-3,4,-1,2,1,-5,4};
  vector < int > subarray;
  int lon = maxSubArray(arr, subarray);
  cout << "The longest subarray with maximum sum is " << lon << endl;
  cout << "The subarray is " << endl;
  for (int i = subarray[0]; i <= subarray[1]; i++) {
    cout << arr[i] << " ";
  }

}

def maxSubArraySum(arr,size):
    
    max_till_now = arr[0]
    max_ending = 0
    
    for i in range(0, size):
        max_ending = max_ending + arr[i]
        if max_ending < 0:
            max_ending = 0
        
        
        elif (max_till_now < max_ending):
            max_till_now = max_ending
            
    return max_till_now

arr = [-2, -3, 4, -1, -2, 5, -3]
print("Maximum Sub Array Sum Is" , maxSubArraySum(arr,len(arr)))