 Logicmojo - Updated Dec 19, 2022
Logicmojo - Updated Dec 19, 2022
Problem Statement: Largest Rectangle in Histogram
Given an array of integers heights representing the histogram's bar height where the width of each bar is 1, return the area of the largest rectangle in the histogram.
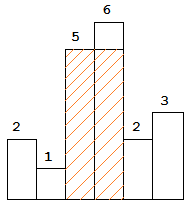
Example:
heights = [2,1,5,6,2,3]
Output: 10
Explanation: The above is a histogram where width of each bar is 1. The largest rectangle is shown in the red area, which has an area = 10 units.

Approach 1: Brute Force
A simple solution is to one by one consider all bars as starting points and calculate area of all rectangles starting with every bar. Finally return maximum of all possible areas. Time complexity of this solution would be O(n2). Since it is not the optimal solution so we need to optimse it.
Approach 2: Using Left Right array(Three pass)
For any bar i the maximum rectangle is of width r - l - 1 where r - is the last coordinate of the bar to the right with height h[r] >= h[i] and l - is the last coordinate of the bar to the left which height h[l] >= h[i]
So if for any i coordinate we know his utmost higher (or of the same height) neighbors to the right and to the left, we can easily find the largest rectangle
The main trick is how to effectively calculate lessFromRight and lessFromLeft arrays. The trivial solution is to use O(n^2) solution and for each i element first find his left/right heighbour in the second inner loop just iterating back or forward
The only line change shifts this algorithm from O(n2) to O(n) complexity: we don't need to rescan each item to the left - we can reuse results of previous calculations and "jump" through indices in quick manner
C++ Implementation:
#include <bits/stdc++.h> using namespace std; class Solution { public: int largestRectangleArea(vector < int > & heights) { int n = heights.size(); stack < int > st; int leftsmall[n], rightsmall[n]; for (int i = 0; i < n; i++) { while (!st.empty() && heights[st.top()] >= heights[i]) { st.pop(); } if (st.empty()) leftsmall[i] = 0; else leftsmall[i] = st.top() + 1; st.push(i); } // clear the stack to be re-used while (!st.empty()) st.pop(); for (int i = n - 1; i >= 0; i--) { while (!st.empty() && heights[st.top()] >= heights[i]) st.pop(); if (st.empty()) rightsmall[i] = n - 1; else rightsmall[i] = st.top() - 1; st.push(i); } int maxA = 0; for (int i = 0; i < n; i++) { maxA = max(maxA, heights[i] * (rightsmall[i] - leftsmall[i] + 1)); } return maxA; } }; int main() { vector<int> heights = {2, 1, 5, 6, 2, 3, 1}; Solution obj; cout << "The largest area in the histogram is " << obj.largestRectangleArea(heights); return 0; }
Python Implementation:
class Solution: def largestRectangleArea(self, arr): if not arr: return 0 left = [0] * len(arr) right = [0] * len(arr) right[-1] = len(arr) left[0] = -1 for i in range(1, len(arr)): p = i - 1 while p >= 0 and arr[p] >= arr[i]: p = left[p] left[i] = p for i in range(len(arr) - 2, -1, -1): p = i + 1 while p < len(arr) and arr[p] >= arr[i]: p = right[p] right[i] = p maxi = 0 for i in range(len(arr)): maxi = max(maxi, (right[i] - left[i] - 1) * arr[i]) return maxi ob1 = Solution() print(ob1.largestRectangleArea([2,1,5,6,2,3]))
Time Complexity:O(3n)~O(n) Since we are doing 3 pass
Auxiliary Space: O(n)+O(n) = O(2n)~O(n), Since we are using left and right array
Approach 3: Using Stack(Single pass)
For given bar i with value h, how to find the biggest rectangle, which is ending with this bar? We need to find the previous smallest place, where value is less or equal than h: that is smallest j, such that j < i and heights[j] >= heights[i]. Ideal data structure for these type of problems is monostack: stack which has the following invariant: elements inside will be always in increasing order.
The stack maintain the indexes of buildings with ascending height. Before adding a new building pop the building who is taller than the new one. The building popped out represent the height of a rectangle with the new building as the right boundary and the current stack top as the left boundary. Calculate its area and update ans of maximum area. Boundary is handled using dummy buildings.
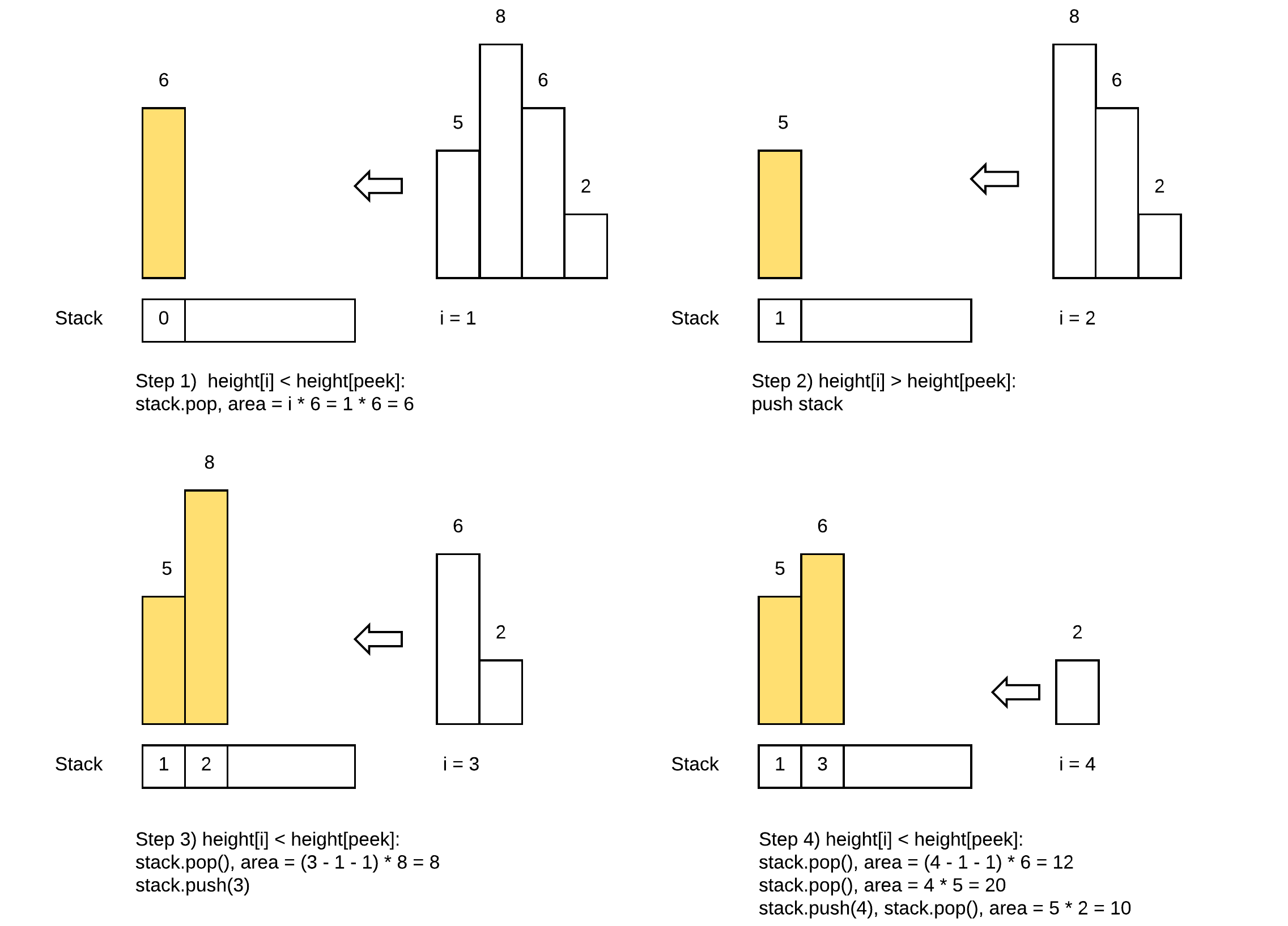
C++ Implementation:
#include <bits/stdc++.h> using namespace std; class Solution { public: int largestRectangleArea(vector < int > & histo) { stack < int > st; int maxA = 0; int n = histo.size(); for (int i = 0; i <= n; i++) { while (!st.empty() && (i == n || histo[st.top()] >= histo[i])) { int height = histo[st.top()]; st.pop(); int width; if (st.empty()) width = i; else width = i - st.top() - 1; maxA = max(maxA, width * height); } st.push(i); } return maxA; } }; int main() { vector < int > histo = {2, 1, 5, 6, 2, 3, 1}; Solution obj; cout << "The largest area in the histogram is " << obj.largestRectangleArea(histo) << endl; return 0; }
Python Implementation:
class Solution: def largestRectangleArea(self, heights): # store x coordination, init as -1 stack = [ -1 ] # add zero as dummy tail heights.append( 0 ) # top index for stack top = -1 # area of rectangle rectangle = 0 # scan each x coordination and y coordination for x_coord, y_coord in enumerate(heights): while heights[ stack[top] ] > y_coord: # current height is lower than previous # update rectangle area from previous heights # get height h = heights[ stack.pop() ] # compute width w = x_coord - stack[top] -1 # update maximal area rectangle = max(rectangle, h * w) # push current x coordination into stack stack.append( x_coord ) return rectangle ob1 = Solution() print(ob1.largestRectangleArea([2,1,5,6,2,3]))
Time Complexity: O(n)
Auxiliary Space: O(n), Since we are using stack for storing
With this article at Logicmojo, you must have the complete idea of solving Largest Rectangle in Histogram problem.