 Logicmojo - Updated Aug 28, 2021
Logicmojo - Updated Aug 28, 2021
Problem Statement: Lowest Common Ancestor in Binary Tree
The lowest common ancestor of two nodes p and q is the lowest node in the binary tree that has p and q as its descendants.
Note: A node is also considered a descendant of itself.
Given the reference to the root node and two nodes p and q in a binary tree, return the reference to the lowest common ancestor of p and q.
Note: You can assume that p and q will be present in the tree.
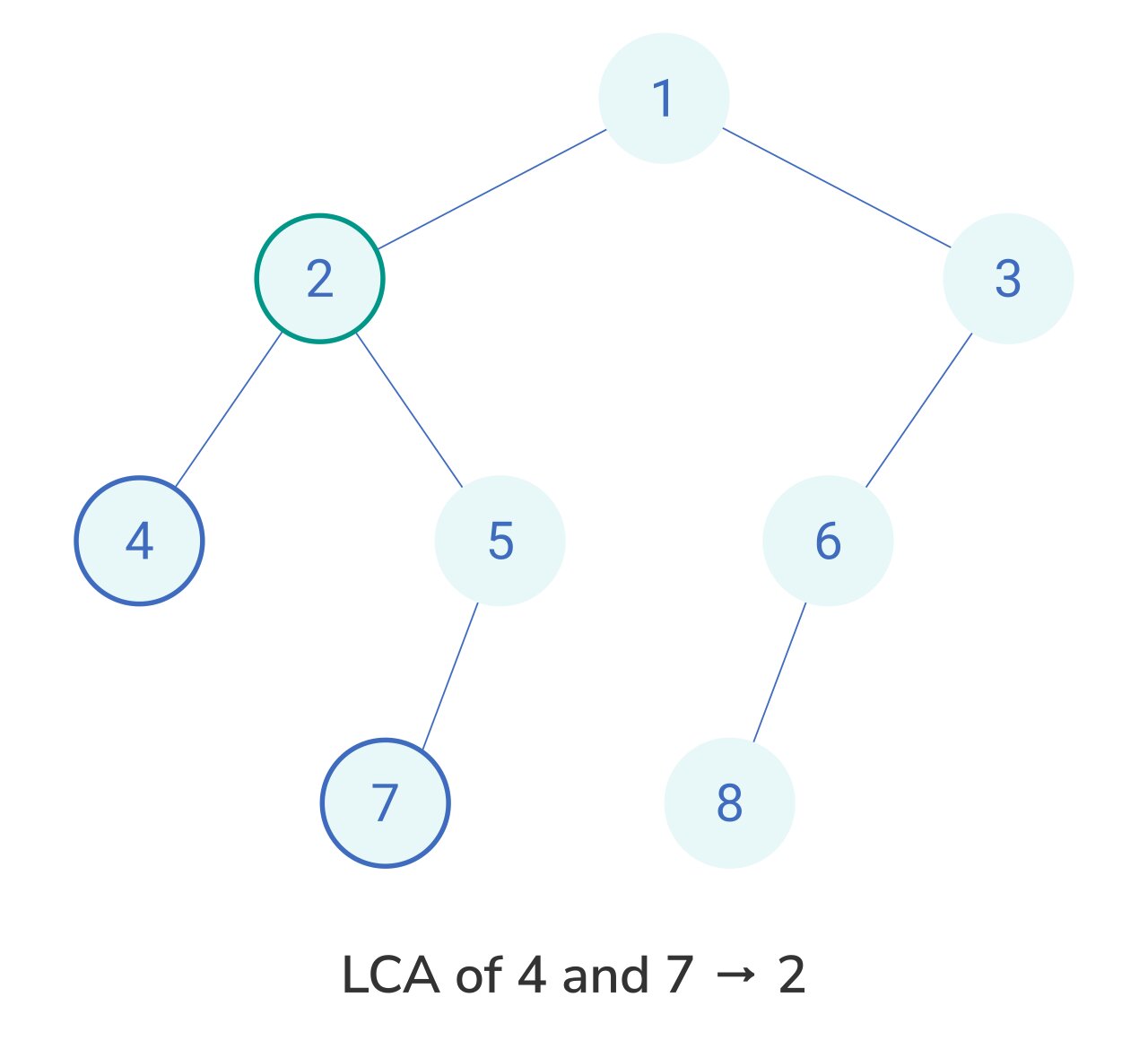
Approach 1: Iterative Tree Traversal
In this method we will iterate from the node p to the root of the tree, while saving the ancestors of the node in a vector. Next, we will iterate from the node q to the root of the tree and determine whether the ancestors of a appear in the ancestors of q. The first ancestor of q which is also an ancestor of p will be the lowest common ancestor. This method will require a total of two traversals of the binary tree.
This method will require a total of two traversals of the binary tree. So the Time-Complexity will be O(2h) ≈ O(h) where h is the height of the tree.
This method will store the ancestors of node a in a vector. So in the worst-case scenario, a is the leaf of the tree at the greatest depth. So a would have h ancestors. The Space-Complexity would hence be O(h).
C++ Implementation:TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { if (!root || root == p || root == q) return root; unordered_map<TreeNode*, TreeNode*> parent; parent[root] = NULL; stack<TreeNode*> stk; stk.push(root); while (!parent[p] || !parent[q]) { TreeNode* node = stk.top(); stk.pop(); if (node->left) { parent[node->left] = node; stk.push(node->left); } if (node->right) { parent[node->right] = node; stk.push(node->right); } } set<TreeNode*> ancestor; while (p) { ancestor.insert(p); p = parent[p]; } while (ancestor.find(q) == ancestor.end()) { q = parent[q]; } return q; }
Python Implementation:
class Node: def __init__(self,val): self.val = val self.left_Node = None self.right_Node = None self.Parent = None class BinaryTree: def __init__(self,val): self.root = Node(val) def lowest_common_ancestor(node1,node2): ancestor_node1 = [] # use slice to store the ancestor of node1 curr = node1 while(curr!=None): curr = curr.Parent if(curr != None): ancestor_node1.append(curr) # add ancestors of node1 curr = node2 while(curr!=None): curr = curr.Parent for i in range(0,len(ancestor_node1)): # find out if the most immediate ancestor of node1 is also the common ancestor of node2 if(ancestor_node1[i]==curr): print ("The nodes ",node1.val," and ",node2.val," have ",curr.val," as their lowest common ancestor") return curr return None def main(): # making the Binary tree structure shown above. BST = BinaryTree('d') BST.root.left_Node = Node('c') BST.root.left_Node.Parent = BST.root BST.root.right_Node = Node('e') BST.root.right_Node.Parent = BST.root BST.root.left_Node.left_Node = Node('a') BST.root.left_Node.left_Node.Parent = BST.root.left_Node BST.root.left_Node.right_Node = Node('b') BST.root.left_Node.right_Node.Parent = BST.root.left_Node BST.root.right_Node.left_Node = Node('f') BST.root.right_Node.left_Node.Parent = BST.root.right_Node BST.root.right_Node.right_Node = Node('g') BST.root.right_Node.right_Node.Parent = BST.root.right_Node result = lowest_common_ancestor(BST.root.right_Node.left_Node,BST.root.right_Node.right_Node) if __name__ == "__main__": main()
Approach 2: Recursive Approach
The approach is pretty intuitive. Traverse the tree in a depth first manner.
Steps :
1. Please note that p and q always exist in the tree.
2. Since we dfs from the root down to its children, if current root == p or root == q then current root must be their LCA.
3. If left subtree contains one of descendant (p or q) and right subtree contains the remaining descendant (q or p) then the root is their LCA.
4. If left subtree contains both p and q then return left as their LCA. If right subtree contains both p and q then return right as their LCA.
C++ Implementation:
class Solution { public: TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { //base case if (root == NULL || root == p || root == q) { return root; } TreeNode* left = lowestCommonAncestor(root->left, p, q); TreeNode* right = lowestCommonAncestor(root->right, p, q); //result if(left == NULL) { return right; } else if(right == NULL) { return left; } else { //both left and right are not null, we found our result return root; } } };
Python Implementation:
# Find LCA class Node: def __init__(self, val): self.val = val self.left = None self.right = None def lca(root, p, q): if root.val == p or root.val == q: return root left = right = None if root.left: left = lca(root.left, p, q) if root.right: right = lca(root.right, p, q) # if both children returned a node, means # both p and q found so parent is LCA if left and right: return root # either one of the chidren returned a node, meaning either p or q founleft or right branch. # Example: assuming 'p' found in left child, right child returned 'None'. This means 'q' is # somewhere below node where 'p' was found we dont need to search all the way, # because in such scenarios, node where 'p' found is LCA else: return left or right root = Node(3) root.left = Node(4) root.right = Node(5) root.left.left = Node(6) root.left.right = Node(7) root.right.left = Node(8) root.right.right = Node(9) print(lca(root, 4, 9).val)
Time-Complexity: O(m+n) ≈ O(n), this method will require one traversal of the binary tree where m is the number of edges and n is the total number of nodes.
Auxiliary Space: O(n)
With this article at Logicmojo, you must have the complete idea of solving Lowest Common Ancestor in Binary Tree problem.