Level Order Traversal of Binary Tree

Name: Merge Overlapping Intervals
Brand: LogicMojo
SKU: .
Availability: InStock
Rating: 4.8 (230 reviews)

Back to home

𝑻𝒂𝒃𝒍𝒆 𝒐𝒇 𝑪𝒐𝒏𝒕𝒆𝒏𝒕

Problem Statement: Level Order Traversal of Binary Tree
Approach 1: Recursive
Approach 2: Using Queue

Logicmojo - Updated Aug 28, 2021

Problem Statement: Level Order Traversal of Binary Tree

Given the root of a binary tree, return the level order traversal of its nodes' values. (i.e., from left to right, level by level).

Level Order Traversal is the algorithm to process all nodes of a tree by traversing through depth, first the root, then the child of the root, etc.

For example, the level order traversal for the following tree is 1, 2, 3, 4, 5, 6, 7:

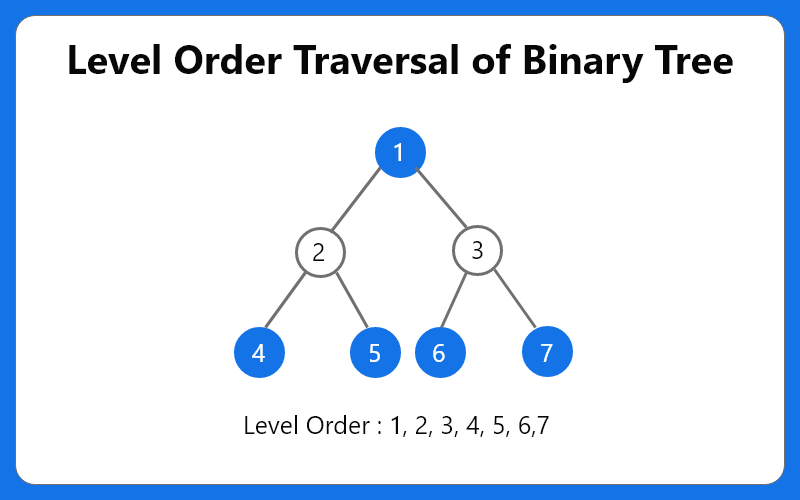
We have presented two approaches to find the two elements:

• Recursive Approach
• Using Queue

Approach 1: Recursive

In this method, there are essentially two functions. One is used to print all nodes at a specific level (CurrentLevel), while the other is used to print the tree's level order traversal (Levelorder).

We obtain the tree's height in the CurrentLevel function and call the LevelOrder function for each level between 1 and height.
We supply two parameters to the LevelOrder function: level and root. The steps are as follows:
1. Return after checking if root is null.
2. Check if level is equal to 1 then print the current root value.
3. Now, call both the children of the current root repeatedly while decreasing the value of level by one.

C++ Implementation:

#include <iostream>
using namespace std;
 
class node {
public:
    int data;
    node *left, *right;
};
node* newNode(int data);
node* newNode(int data)
{
    node* Node = new node();
    Node->data = data;
    Node->left = NULL;
    Node->right = NULL;
 
    return (Node);
}
 
int height(node* node) {
    if (node == NULL)
        return 0;
    else {
        int lheight = height(node->left);
        int rheight = height(node->right);
        if (lheight > rheight) {
            return(lheight + 1);
        }
        else {
          return(rheight + 1);
        }
    }
}
 
void CurrentLevel(node* root, int level) {
    if (root == NULL)
        return;
    if (level == 1)
        cout << root->data << " ";
    else if (level > 1) {
       CurrentLevel(root->left, level-1);
       CurrentLevel(root->right, level-1);
    }
}
 
void LevelOrder(node* root) {
    int h = height(root);
    int i;
    for (i = 1; i <= h; i++)
     CurrentLevel(root, i);
}
 
 
 
int main() {
	node* root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(4);
    root->left->right = newNode(5);
    
    LevelOrder(root);
	return 0;
}

Java Implementation:

class Node {
	int data;
	Node left, right;
	public Node(int item)
	{
		data = item;
		left = right = null;
	}
}

class Main {
	Node root;

	public Main() { root = null; }

	void LevelOrder()
	{
        int h = height(root);
        int i;
        for (i=1; i<=h; i++)
            CurrentLevel(root, i);
	}
	int height(Node root) {
    	if (root == null)
        	  return 0; 
    	else {
       		int lheight = height(root.left);
       		int rheight = height(root.right);
       		if (lheight > rheight)
            	return(lheight+1);
       		else return(rheight+1);
    	}
	}
	void CurrentLevel (Node root ,int level) {
     	if (root == null){
        	    return;
		}
     	if (level == 1){
        	  System.out.print(root.data + " ");
		}
     	else if (level > 1) {
        	CurrentLevel(root.left, level-1);
        	CurrentLevel(root.right, level-1);
     	 }
	}
	public static void main(String args[])
	{
		Main tree = new Main();
		tree.root = new Node(1);
		tree.root.left = new Node(2);
		tree.root.right = new Node(3);
		tree.root.left.left = new Node(4);
		tree.root.left.right = new Node(5);

		tree.LevelOrder();

	}
}

Python Implementation:

class Node:
    def __init__(self, key):
        self.data = key
        self.left = None
        self.right = None

def LevelOrder(root):
    h = height(root)
    for i in range(1, h+1):
        CurrentLevel(root, i)
def CurrentLevel(root , level):
    if root is None:
        return
    if level == 1:
        print(root.data,end=" ")
    elif level > 1 :
        CurrentLevel(root.left , level-1)
        CurrentLevel(root.right , level-1)
def height(node):
    if node is None:
        return 0
    else :
        lheight = height(node.left)
        rheight = height(node.right)
        if lheight > rheight :
            return lheight+1
        else:
            return rheight+1


root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
LevelOrder(root)

Time complexity: For a skewed tree, time complexity will be O(n^2).

Space complexity: For a skewed tree space complexity will be O(n) and for a Balanced tree, the call stack uses O(log n) space, (i.e., the height of the balanced tree).

Approach 2: Using Queue

Now the question is: can we optimize the time complexity of the level order traversal? Can we traverse tree level by level in O(n) time complexity? Think!

Let's have a look at the node order in level order traversal.

At level 0, we process the root node first, followed by the left and right children at level 1. (assuming the order from left to right).
Similarly, at the second level, we first process the children of the left child of the root then process the children of the right child. This process goes on for all the levels in the tree.

So one idea is clear: at any given level, the node which will be processed first, the children of that node will be processed first at the next level. So this is the First In First Out Order (FIFO Order) of processing nodes! So we can use the queue data structure to simulate the BFS traversal.

Algorithm

levelorder(root):
    q —> empty queue
    q.enqueue(root)
    while (not q.isEmpty())
        node —> q.dequeue()
        visit(node)
        if (node.left != null)
            q.enqueue(node.left)
        if (node.right != null)
            q.enqueue(node.right)

C++ Implementation:

#include <bits/stdc++.h>
using namespace std;

struct Node {
	int data;
	struct Node *left, *right;
};

void printLevelOrder(Node* root)
{
	if (root == NULL)
		return;

	queue<Node*> q;
	q.push(root);

	while (q.empty() == false) {
		Node* node = q.front();
		cout << node->data << " ";
		q.pop();

		if (node->left != NULL)
			q.push(node->left);

		if (node->right != NULL)
			q.push(node->right);
	}
}

Node* newNode(int data)
{
	Node* temp = new Node;
	temp->data = data;
	temp->left = temp->right = NULL;
	return temp;
}
int main()
{
	Node* root = newNode(1);
	root->left = newNode(2);
	root->right = newNode(3);
	root->left->left = newNode(4);
	root->left->right = newNode(5);

	printLevelOrder(root);
	return 0;
}

Java Implementation:

import java.util.LinkedList;
import java.util.Queue;

class Node {
	int data;
	Node left, right;

	public Node(int item)
	{
		data = item;
		left = null;
		right = null;
	}
}

class BinaryTree {

	Node root;
	void printLevelOrder()
	{
		Queue<Node> queue = new LinkedList<Node>();
		queue.add(root);
		while (!queue.isEmpty()) {

			Node tempNode = queue.poll();
			System.out.print(tempNode.data + " ");

			if (tempNode.left != null) {
				queue.add(tempNode.left);
			}

			if (tempNode.right != null) {
				queue.add(tempNode.right);
			}
		}
	}

	public static void main(String args[])
	{
		BinaryTree tree_level = new BinaryTree();
		tree_level.root = new Node(1);
		tree_level.root.left = new Node(2);
		tree_level.root.right = new Node(3);
		tree_level.root.left.left = new Node(4);
		tree_level.root.left.right = new Node(5);

		tree_level.printLevelOrder();
	}
}

Python Implementation:

class Node:
	def __init__(self, key):
		self.data = key
		self.left = None
		self.right = None

def printLevelOrder(root):
	if root is None:
		return

	queue = []
	queue.append(root)

	while(len(queue) > 0):

		print(queue[0].data)
		node = queue.pop(0)

		if node.left is not None:
			queue.append(node.left)
		if node.right is not None:
			queue.append(node.right)
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)

printLevelOrder(root)

Time Complexity: O(N) where n is the number of nodes in the binary tree.

Space Complexity: O(N) where n is the number of nodes in the binary tree.

With this article at Logicmojo, you must have the complete idea of solving Level Order Traversal of a Binary Tree problem.