LRU Cache

Back to home
Logicmojo - Updated Aug 28, 2021



Problem Statement: LRU Cache

lru cache : Implement Least Recently Used (LRU) cache. You need to implement the following for the LRUCache class:

LRUCache(int capacity) initializes the cache to store data of size: capacity.


int get(int key) returns the value of the key if it exists, otherwise returns -1.

void add(int key, int value) updates the value of the key if the key exists.

Otherwise, add the key-value pair to the cache. If the number of keys exceeds the capacity from this operation, evict the least recently used key.

Note: Try to achieve each operation in O(1) time complexity.


Approach: Using Hashmap and LinkedList


This is one of the favourite interview question where the interviewer demands a comprehensive explanation of the working principle.Try to explain it in a step-by-step manner.

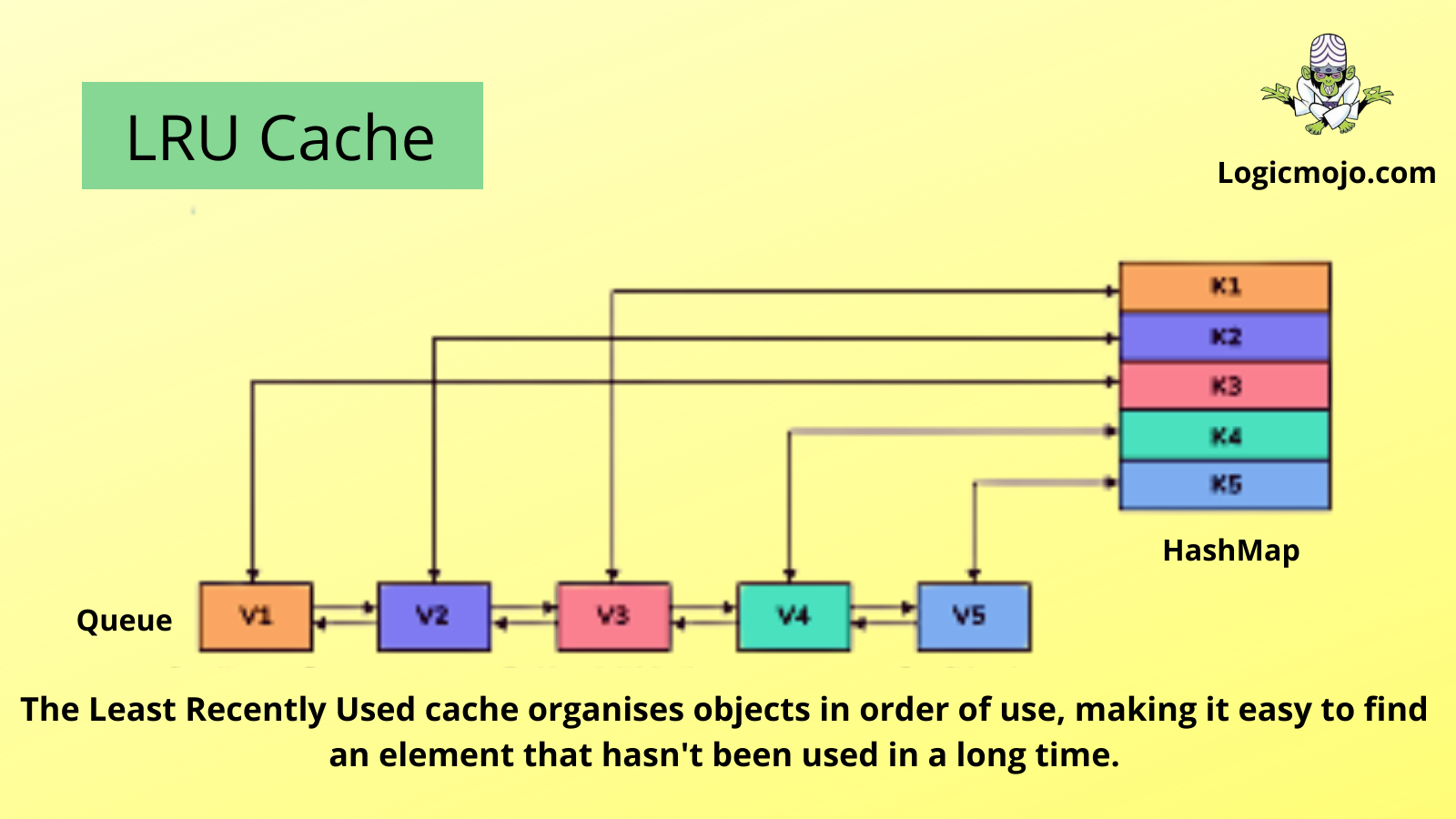
An LRU cache is built by combining two data structures: a doubly linked list and a hash map


We'll set up our linked list with the most-recently used item at the head of the list and the least-recently used item at the tail


The most frequent operation of the problem is changing the node position in the list. Change position of the node means two operations, delete and insert. Double linked list data structure takes constant time O(1) to insert or delete nodes a linked list by repointing the previous and next pointer of the node.


How get(key) works?

 • If the cache contains this key

 • Get the node from the cache.

 • Now this node is recently accessed, we will delete the existing node from the queue and add it to the end.

 • Return the value of this key from the cache.

 • If cache does not contain this key, then return -1

How set(key,value) works?

 • There are 3 cases to consider in this:

Case1:

 • If cache already contains this key:

 • Create a new node using the key and value;

 • Get the old node from the cache for this key.

 • Delete it from the queue.

 • Add new node to the end of the queue. This is because it is recently accessed.

 • Update the cache with the new node (value for the existing key).

Case2:

 • If the capacity of the cache is > 0 i.e (cache is still not full)

 • Create a new node using the key and value

 • Store in the cache.

 • Add the new node to the end of the queue.

Case3:

 • If the capacity is full

 • Get the first element in the queue. This is the least recently used element

 • Remove this element from the cache.

 • Create a new node using the given key and value.

 • Add to cache the key and the new node.

 •Add the new node to the end of the queue.



C++ Implementation:

class LRUCache {
  public:
    class node {
      public:
        int key;
      int val;
      node * next;
      node * prev;
      node(int _key, int _val) {
        key = _key;
        val = _val;
      }
    };

  node * head = new node(-1, -1);
  node * tail = new node(-1, -1);

  int cap;
  unordered_map < int, node * > m;

  LRUCache(int capacity) {
    cap = capacity;
    head -> next = tail;
    tail -> prev = head;
  }

  void addnode(node * newnode) {
    node * temp = head -> next;
    newnode -> next = temp;
    newnode -> prev = head;
    head -> next = newnode;
    temp -> prev = newnode;
  }

  void deletenode(node * delnode) {
    node * delprev = delnode -> prev;
    node * delnext = delnode -> next;
    delprev -> next = delnext;
    delnext -> prev = delprev;
  }

  int get(int key_) {
    if (m.find(key_) != m.end()) {
      node * resnode = m[key_];
      int res = resnode -> val;
      m.erase(key_);
      deletenode(resnode);
      addnode(resnode);
      m[key_] = head -> next;
      return res;
    }

    return -1;
  }

  void put(int key_, int value) {
    if (m.find(key_) != m.end()) {
      node * existingnode = m[key_];
      m.erase(key_);
      deletenode(existingnode);
    }
    if (m.size() == cap) {
      m.erase(tail -> prev -> key);
      deletenode(tail -> prev);
    }

    addnode(new node(key_, value));
    m[key_] = head -> next;
  }
};


Python Implementation:

class ListNode:
    def __init__(self, key, value):
        self.key = key
        self.value = value
        self.prev = None
        self.next = None

class LRUCache:

    def __init__(self, capacity: int):
        self.dic = dict() # key to node
        self.capacity = capacity
        self.head = ListNode(0, 0)
        self.tail = ListNode(-1, -1)
        self.head.next = self.tail
        self.tail.prev = self.head

    def get(self, key):
        if key in self.dic:
            node = self.dic[key]
            self.removeFromList(node)
            self.insertIntoHead(node)
            return node.value
        else:
            return -1

    def put(self, key, value):
        if key in self.dic:             # similar to get()        
            node = self.dic[key]
            self.removeFromList(node)
            self.insertIntoHead(node)
            node.value = value         # replace the value len(dic)
        else: 
            if len(self.dic) >= self.capacity:
                self.removeFromTail()
            node = ListNode(key,value)
            self.dic[key] = node
            self.insertIntoHead(node)
    def removeFromList(self, node):
        node.prev.next = node.next
        node.next.prev = node.prev
    
    def insertIntoHead(self, node):
        headNext = self.head.next 
        self.head.next = node 
        node.prev = self.head 
        node.next = headNext 
        headNext.prev = node
    
    def removeFromTail(self):
        if len(self.dic) == 0: return
        tail_node = self.tail.prev
        del self.dic[tail_node.key]
        self.removeFromList(tail_node)
        
cache = LRUCache(2)
cache.put(1, 1)
cache.put(2, 2)
cache.get(1)
cache.put(3, 3)
cache.get(2)
cache.put(4, 4)
print(cache.get(1))
print(cache.get(3))
print(cache.get(4))

Time Complexity: O(1) for all operations

Space Complexity: O(n) where n is the size of cache

With this article at Logicmojo, you must have the complete idea of solving LRU Cache problem.
© 2020 Logicmojo. ALL RIGHTS RESERVED