 Logicmojo - Updated Aug 28, 2021
Logicmojo - Updated Aug 28, 2021
Problem Statement: Majority Element
Write a function which takes an array and prints the majority element (if it exists), otherwise prints "No Majority Element". A majority element in an array arr[] of size n is an element that appears more than n/2 times (and hence there is at most one such element).
Given an array arr of size n, return the majority element
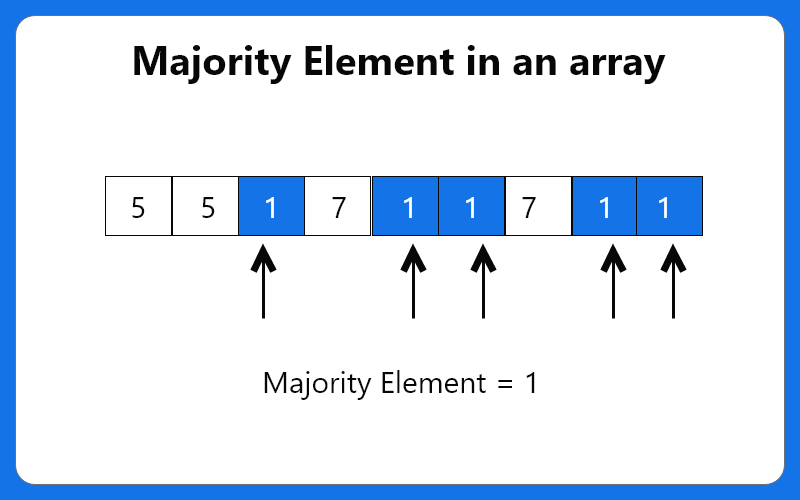
Input : {5, 5, 1, 7, 1, 1, 7, 1, 1}
Output : 1
Explanation : The frequency of 1 is 5 which is greater than the half of the size of the array size.
Input : {1, 1, 9, 5, 9, 9, 5, 9}
Output : No Majority Element
Explanation : There is no element whose frequency is greater than the half of the size of the array size.
We have presented three approaches to find the majority element:
• Naive Approach• Using Moore's Voting Algorithm
• Using Hashmap
Naive Approach
The basic solution is to have two loops and keep track of the maximum count for all different elements. If maximum count becomes greater than n/2 then break the loops and return the element having maximum count. If the maximum count doesn’t become more than n/2 then the majority element doesn’t exist.
Time Complexity: O(n*n).
A nested loop is needed where both the loops traverse the array from start to end, so the time complexity is O(n^2).
Auxiliary Space: O(1).
As no extra space is required for any operation so the space complexity is constant.
C++ Implementation:
#include <bits/stdc++.h> using namespace std; void majorityElement(int arr[], int n) { int max = 0; int index=-1,i=0; for (i = 0; i < n; i++) { int count = 0; for (int j = 0; j < n; j++) { if (arr[i] == arr[j]) count++; } if (count > n/2) { index=i; break; } } if (index!=-1) cout << arr[index] << endl; else cout << "No Majority Element" << endl; } int main() { //int arr[] = {5, 5, 1, 7, 1, 1, 7, 1, 1}; int arr[] = {1, 1, 9, 5, 9, 9, 5, 9}; int n = sizeof(arr) / sizeof(arr[0]); majorityElement(arr, n); return 0; }
Java Implementation:
class Main { public static void majorityElement (int arr[], int n){ int max = 0; int index = -1, i = 0; for (i = 0; i < n; i++){ int count = 0; for (int j = 0; j < n; j++){ if (arr[i] == arr[j]) count++; } if (count > n / 2){ index = i; break; } } if (index != -1) System.out.println (arr[index]); else System.out.println ("No Majority Element"); } public static void main (String[]args){ int arr[] = { 5, 5, 1, 7, 1, 1, 7, 1, 1 }; //int arr[] = {1, 1, 9, 5, 9, 9, 5, 9}; int n = arr.length; majorityElement (arr, n); } }
Python Implementation:
def findMajority(arr, n): maxCount = 0 index = -1 # sentinels for i in range(n): count = 0 for j in range(n): if(arr[i] == arr[j]): count += 1 if(count > maxCount): maxCount = count index = i if (maxCount > n//2): print(arr[index]) else: print("No Majority Element")
Using Moore’s Voting Algorithm
This is a two-step process.
1. The first step gives the element that maybe the majority element in the array. If there is a majority element in an array, then this step will definitely return majority element, otherwise, it will return candidate for majority element.
2. Check if the element obtained from the above step is majority element. This step is necessary as there might be no majority element.
Time Complexity: O(n).
As two traversal of the array is needed, so the time complexity is linear.
Auxiliary Space: O(1).
As no extra space is required.
C++ Implementation:
#include <bits/stdc++.h> using namespace std; int findCandidate(int arr[], int size) { int maj_index = 0, count = 1; for (int i = 1; i < size; i++) { if (arr[maj_index] == arr[i]) count++; else count--; if (count == 0) { maj_index = i; count = 1; } } return arr[maj_index]; } bool isMajority(int arr[], int size, int cand) { int count = 0; for (int i = 0; i < size; i++) if (arr[i] == cand) count++; if (count > size / 2) return 1; else return 0; } void printMajority(int arr[], int size) { int cand = findCandidate(arr, size); if (isMajority(arr, size, cand)) cout << " " << cand << " "; else cout << "No Majority Element"; } int main() { //int arr[] = { 5, 5, 1, 7, 1, 1, 7, 1, 1 }; int arr[] = {1, 1, 9, 5, 9, 9, 5, 9}; int size = (sizeof(arr)) / sizeof(arr[0]); printMajority(arr, size); return 0; }
Java Implementation:
class Main { static void printMajority(int arr[], int size){ int cand = findCandidate(arr, size); if (isMajority(arr, size, cand)) System.out.println(" " + cand + " "); else System.out.println("No Majority Element"); } static int findCandidate(int arr[], int size){ int maj_index = 0, count = 1; int i; for (i = 1; i < size; i++) { if (arr[maj_index] == arr[i]) count++; else count--; if (count == 0) { maj_index = i; count = 1; } } return arr[maj_index]; } static boolean isMajority(int arr[], int size, int cand) { int i, count = 0; for (i = 0; i < size; i++) { if (arr[i] == cand) count++; } if (count > size / 2) return true; else return false; } public static void main(String[] args) { //int arr[] = { 5, 5, 1, 7, 1, 1, 7, 1, 1 }; int arr[] = {1, 1, 9, 5, 9, 9, 5, 9}; int size = arr.length; printMajority(arr, size); } }
Python Implementation:
def findCandidate(A): maj_index = 0 count = 1 for i in range(len(A)): if A[maj_index] == A[i]: count += 1 else: count -= 1 if count == 0: maj_index = i count = 1 return A[maj_index] def isMajority(A, cand): count = 0 for i in range(len(A)): if A[i] == cand: count += 1 if count > len(A)/2: return True else: return False def printMajority(A): cand = findCandidate(A) if isMajority(A, cand) == True: print(cand) else: print("No Majority Element") A = [5, 5, 1, 7, 1, 1, 7, 1, 1] printMajority(A)
Using Hashmap
This method is somewhat similar to Moore voting algorithm in terms of time complexity, but in this case, there is no need for the second step of Moore voting algorithm. But as usual, here space complexity becomes O(n). In Hashmap(key-value pair), at value, maintain a count for each element(key) and whenever the count is greater than half of the array length, return that key(majority element).
The steps are:
• Create a hashmap to store a key-value pair, i.e. element-frequency pair.
• Traverse the array from start to end.
• For every element in the array, insert the element in the hashmap if the element does not exist as key,else fetch the value of the key ( array[i] ), and increase the value by 1
• If the count is greater than half then print the majority element and break.
• If no majority element is found print "No Majority element"
Time Complexity :O(n)
One traversal of the array is needed, so the time complexity is linear.
Space Complexity : O(n)
Since a hashmap requires linear space.
C++ Implementation:
#include <bits/stdc++.h> using namespace std; void findMajority(int arr[], int size) { unordered_map<int, int> m; for(int i = 0; i < size; i++) m[arr[i]]++; int count = 0; for(auto i : m) { if(i.second > size / 2) { count =1; cout<< i.first<<endl; break; } } if(count == 0) cout << "No Majority element" << endl; } int main() { //int arr[] = { 5, 5, 1, 7, 1, 1, 7, 1, 1 }; int arr[] = {1, 1, 9, 5, 9, 9, 5, 9}; int n = sizeof(arr) / sizeof(arr[0]); findMajority(arr, n); return 0; }
Java Implementation:
import java.util.HashMap; class Main { private static void findMajority(int[] arr) { HashMap<Integer,Integer> map = new HashMap<Integer, Integer>(); for(int i = 0; i < arr.length; i++) { if (map.containsKey(arr[i])) { int count = map.get(arr[i]) +1; if (count > arr.length /2) { System.out.println(arr[i]); return; } else map.put(arr[i], count); } else map.put(arr[i],1); } System.out.println(" No Majority element"); } public static void main(String[] args) { int arr[] = { 5, 5, 1, 7, 1, 1, 7, 1, 1 }; //int arr[] = {1, 1, 9, 5, 9, 9, 5, 9}; findMajority(arr); } }
Python Implementation:
def findMajority(arr, size): m = {} for i in range(size): if arr[i] in m: m[arr[i]] += 1 else: m[arr[i]] = 1 count = 0 for key in m: if m[key] > size / 2: count = 1 print(key) break if(count == 0): print("No Majority element") arr = [5, 5, 1, 7, 1, 1, 7, 1, 1 ] n = len(arr) findMajority(arr, n)
With this article at Logicmojo, you must have the complete idea of solving Majority element problem.
