Maximum Path Sum of Binary Tree

Back to home

𝑻𝒂𝒃𝒍𝒆 𝒐𝒇 𝑪𝒐𝒏𝒕𝒆𝒏𝒕

Problem Statement: Maximum Path Sum of Binary Tree
Naive Approach
Approach 2: Using Recursion

Logicmojo - Updated Aug 28, 2021

Problem Statement: Maximum Path Sum of Binary Tree

Given a binary tree, find the maximum path sum. The path may start and end at any node in the tree.

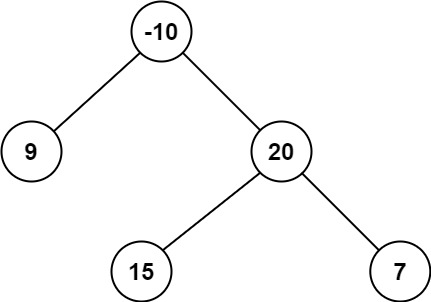
Output: 42

Explanation: The optimal path is 15 -> 20 -> 7 with a path sum of 15 + 20 + 7 = 42.

Approach 1: Brute Force

Traverse left and right subtree of each node and calculate maximum possible sum path. We can update the max path sum passing through each node n in the tree by traversing the n's left subtree and right subtree.

Algorithm:

1. Assume we have nodes numbered 1 to N

2. sum(i) = Maximum sum of a path containing node(i). Clearly the solution of the problem is max(sum(1), sum(2), ...., sum(N))

3. Now, what is the maximum sum of a path containing a particular node(i)?

4. left_result: maximum path sum starting at node(i).left; right_result: maximum path sum starting at node(i).right; sum(i) = max(left_result, 0) + max(right_result, 0) + node(i).val

Time Complexity would be O(n²) and space complexity would be O(n)

Approach 2: Using Recursive Approach

The above approach is also recursive in nature but not the optimal one so to approve the solution we need to think on some important points in above solution, i.e. how can we try to compute the max sum for any node if you have the max sum for their left and right sub-tree?

Each node can be the root of the final maximum path sum. The root here means the topmost node in a path. We calculate the maximum Path Sum rooted at each node and update the max sum during the traversal.

There can only be four different cases when a particular node is involved in the max path.

1. If its the only Node

2. Max path through Left Child + Node

3. Max path through right Child + Node

4. Max path through Left Child + Node + Right Child

C++ Implementation:

#include <bits/stdc++.h>

using namespace std;

struct node {
  int data;
  struct node * left, * right;
};

int findMaxPathSum(node * root, int & maxi) {
  if (root == NULL) return 0;

  int leftMaxPath = max(0, findMaxPathSum(root -> left, maxi));
  int rightMaxPath = max(0, findMaxPathSum(root -> right, maxi));
  int val = root -> data;
  maxi = max(maxi, (leftMaxPath + rightMaxPath) + val);
  return max(leftMaxPath, rightMaxPath) + val;

}

int maxPathSum(node * root) {
  int maxi = INT_MIN;
  findMaxPathSum(root, maxi);
  return maxi;

}

struct node * newNode(int data) {
  struct node * node = (struct node * ) malloc(sizeof(struct node));
  node -> data = data;
  node -> left = NULL;
  node -> right = NULL;

  return (node);
}

int main() {

  struct node * root = newNode(-10);
  root -> left = newNode(9);
  root -> right = newNode(20);
  root -> right -> left = newNode(15);
  root -> right -> right = newNode(7);

  int answer = maxPathSum(root);
  cout << "The Max Path Sum for this tree is " << answer;

  return 0;
}

        Try it Yourself

Python Implementation:

class TreeNode:
    def __init__(self, val=0, left=None, right=None):
        self.val = val
        self.left = left
        self.right = right
class Solution:
    def maxPathSum(self, root: TreeNode) -> int:
        self.result = root.val
        def maxpath(node):
            if not node: return 0
            x = node.val
            l = max(0,maxpath(node.left )) # ignore "left" branch if negative
            r = max(0,maxpath(node.right)) # ignore "right" branch if negative
            self.result = max(self.result, x+l+r ) # Check if merged arc-path (left+node+right) beats the current result
            return max(x+l,x+r) # Try to build maximum branch value
        maxpath(root)
        return self.result

if __name__=='__main__':
    root = TreeNode(10) 
    root.left = TreeNode(2)
    root.right = TreeNode(15)
    root.left.left = TreeNode(-4)
    root.left.right = TreeNode(-6) 
    root.left.left.left = TreeNode(28)
    root.left.left.right = TreeNode(-22)
    root.right.right = TreeNode(-25)
    root.right.right.left = TreeNode(3)
    root.right.right.right = TreeNode(4)
    ob1 = Solution()
    print(ob1.maxPathSum(root))

        Try it Yourself

Time Complexity: O(N), where N is the total number of nodes.

Space Complexity: Space is needed for the recursion stack. In the worst case (skewed tree), space complexity can be O(N).

With this article at Logicmojo, you must have the complete idea of solving Maximum Path Sum of Binary Tree problem.