Merge Overlapping Intervals

Problem Statement: Merge Overlapping Intervals

The problem statement is: Given a list of intervals, merge them to get a list of non-overlapping intervals.

interval = [start, end]

Example:

Intervals: [[1, 2], [2, 3], [1, 4], [5, 6]]

[1, 2] and [2, 3] can be merged to form [1, 3].

Now, [1, 3] and [1, 4] can be merged to form [1, 4].

[1, 4] and [5, 6] have no intersection.

Hence above intervals are merged to form: [[1, 4], [5, 6]]

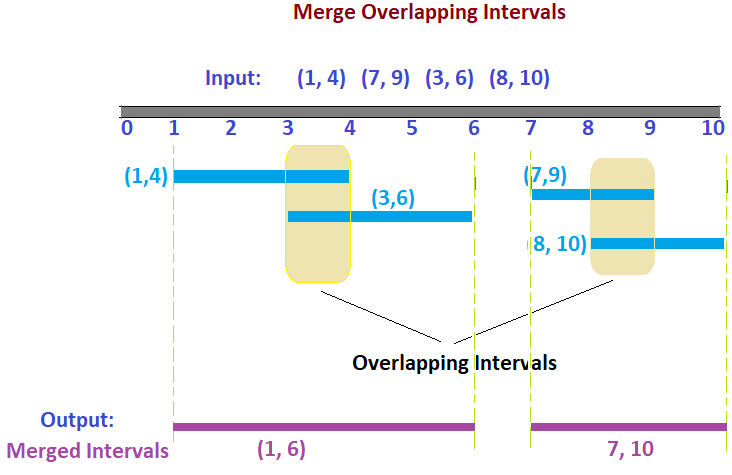
We have presented two approaches to find the two elements:

Approach 1: Brute Force

The goal of this problem is to return a list containing merged intervals for a given list of intervals. Before diving into anything, we would have to define what "overlapping" is in order to solve this problem.

Two intervals overlap if:

1. Interval_1's start time <= Interval_2's start time

2. Interval_1's end time >= Interval_2's start time

Using this idea, we can easily use a nested forloop to go through each possible item and comparing with all other intervals. We would use the conditions above to see if we can merge, and add the output to the answer array. On top of that, we would have to sort our output array if our output array needs to be sorted based on the starting time.

The overall runtime complexity would be O(N²) due to the nested forloop which is not optimal so let's see the optimal.

Approach 2: Efficient- Sorting

if we sort the array from the start, every element to the right will have either a greater or equal start time, so you only need to compare with the next items and merge as you go. You would first have to sort the array, then do a linear pass on the input to merge intervals.

class Solution {
public:
    vector<vector<int>> merge(vector<vector<int>>& intervals) {
        sort(intervals.begin(), intervals.end());
        
        vector<vector<int>> res; 
        
        for (const auto& interval: intervals) {
            if (res.empty()) res.push_back(interval);
            else {
                if (res.back()[1] < interval[0]) res.push_back(interval);
                else res.back()[1] = max(res.back()[1], interval[1]);
            }
        }
        
        return res;
    }
};

class Solution:
    def merge(self, arr: List[List[int]]) -> List[List[int]]:
        arr.sort(key = lambda x: x[0])
        merge = []
        for interval in arr:
            if not merge or merge[-1][1] < interval[0]:
                merge.append(interval)
            else:
                merge[-1][1] = max(merge[-1][1], interval[1])
        return merge

Time Complexity: O(NlogN) logN for sorting and N for traversal

Space Complexity: O(1) No extra space is used.