A spanning tree is a subset of an undirected Graph that has all the vertices connected by minimum number of edges. If all the vertices are connected in a graph, then there exists at least one spanning tree. In a graph, there may exist more than one spanning tree.

Properties
 • A spanning tree does not have any cycle.
 • Any vertex can be reached from any other vertex

What is Minimum Spanning Tree?

A Minimum Spanning Tree(MST) is a subset of edges of a connected weighted undirected graph that connects all the vertices together with the minimum possible total edge weight. To derive an MST, Prim’s algorithm or Kruskal’s algorithm can be used.

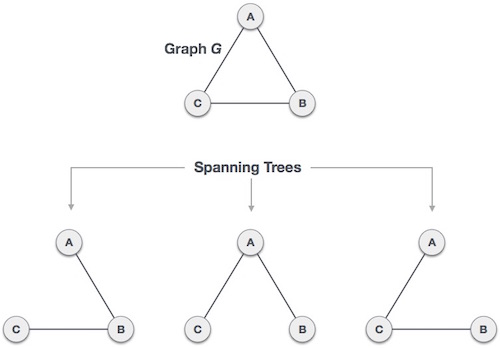
We found three spanning trees off one complete graph. A complete undirected graph can have maximum n^n-2 number of spanning trees, where n is the number of nodes. In the above addressed example, n is 3, hence 3³⁻² = 3 spanning trees are possible.

• It is a tree (i.e., it is acyclic).
• It covers all the vertices V – contains |V| — 1 edges.
• The total cost associated with tree edges is the minimum among all possible spanning trees.
• not necessarily unique.

Properties of Spanning Tree

We now understand that one graph can have more than one spanning tree. Following are a few properties of the spanning tree connected to graph G −

• A connected graph G can have more than one spanning tree.

• All possible spanning trees of graph G, have the same number of edges and vertices.

• The spanning tree does not have any cycle (loops).

• Removing one edge from the spanning tree will make the graph disconnected, i.e. the spanning tree is minimally connected.

• Adding one edge to the spanning tree will create a circuit or loop, i.e. the spanning tree is maximally acyclic.

Mathematical Properties of Spanning Tree

• Spanning tree has n-1 edges, where n is the number of nodes (vertices).

• From a complete graph, by removing maximum e - n + 1 edges, we can construct a spanning tree.

• A complete graph can have maximum n^{n - 2} number of spanning trees.

Application of Spanning Tree

Spanning tree is basically used to find a minimum path to connect all nodes in a graph. Common application of spanning trees are −
• Civil Network Planning
• Computer Network Routing Protocol
• Cluster Analysis

The following algorithms are used to find the minimum spanning tree from a graph, which you can read about in the links below.

Prim's Algorithm
Krushkal’s Algorithm

With this article at Logicmojo, you must have the complete idea of analyzing Minimum Spanning Tree

Good Luck & Happy Learning!!