Minimum Swaps To Make Palindrome

Name: Merge Overlapping Intervals
Brand: LogicMojo
SKU: .
Availability: InStock
Rating: 4.8 (230 reviews)

Back to home

𝑻𝒂𝒃𝒍𝒆 𝒐𝒇 𝑪𝒐𝒏𝒕𝒆𝒏𝒕

Problem Statement: Minimum Swaps To Make Palindrome
Two Pointer Approach

Logicmojo - Updated Aug 28, 2021

Problem Statement: Minimum Swaps To Make Palindrome

Let's say we have a string s and we need to find the minimum number of adjacent swaps to convert it to a palindrome. Return -1 if there is no method to solve the problem.

A palindrome is a string of letter which is equal to itself when reversed.

Input Format: First line of input contain a string str.
Output Format :Integer value which is the Minimum number of adjacent swaps required to convert the string into palindrome.

Example :
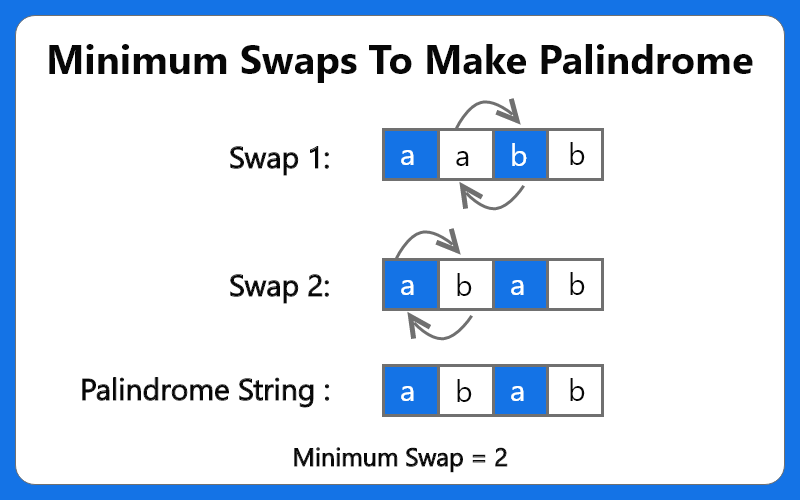
Input: "aabb"
Ouput: 2
Explanation: We can swap the middle "a" and "b" and then swap the first two "a" and "b" to get "baab".

Input: adbcdbad
Output: -1
Explanation: we can't make this string as palindrome by swaping the characters.Hence, the output is -1.

Learn More️

Two Pointer Approach

The steps to solving this problem are outlined below.

Consider a two-pointer with the first pointer tracking from the left side of the string and the second pointer tracking from the right side.
Continue sliding the right cursor one step left until we discover the same character.
Return -1 if the identical character cannot be found.
If the same character found then swap the right pointer’s character towards the right until it is not placed at its correct position in a string.
Increase left pointer and repeat step 2.

C++ Implementation:

#include <bits/stdc++.h>
using namespace std;

int countSwap(string s)
{
	int n = s.length();

	int count = 0;

	for (int i = 0; i < n / 2; i++) {
		int left = i;

		int right = n - left - 1;

		while (left < right) {
			if (s[left] == s[right]) {
				break;
			}
			else {
				right--;
			}
		}

		if (left == right) {
			return -1;
		}

		for (int j = right; j < n - left - 1; j++) {
			swap(s[j], s[j + 1]);
			count++;
		}
	}

	return count;
}

int main()
{
	string s = "aabb";

	int ans1 = countSwap(s);
	reverse(s.begin(), s.end());
	int ans2 = countSwap(s);

	cout << max(ans1, ans2);

	return 0;
}

Java Implementation:

import java.util.*;
import java.io.*;

class Main {
    static int countSwap(String str)
    {
	    int n = str.length();
    	char[] s = str.toCharArray();
    	int count = 0;

	    for (int i = 0; i < n / 2; i++) {
	        int left = i;
    	    int right = n - left - 1;
	      
	        while (left < right) {
        		if (s[left] == s[right]) {
            		break;
		        }
		        else {
	    	        right--;
		        }
	        }

	        if (left == right) {
		        return -1;
	        }
	        else {
		        for (int j = right; j < n - left - 1; j++) {
    		        char t = s[j];
	    	        s[j] = s[j + 1];
		            s[j + 1] = t;
		            count++;
		        }
	        }
	    }
	    return count;
    }
    static void reverse(char a[])
    {
	    int n=a.length;
	    char[] b = new char[n];
	    int j = n;
	    for (int i = 0; i < n; i++) {
	        b[j - 1] = a[i];
	        j = j - 1;
	    }
    }

    public static void main(String[] args)
    {
	    String s = "aabb";
    	int ans1 = countSwap(s);

	    char[] charArray = s.toCharArray();
	    reverse(charArray);
	    s = new String(charArray);

	    int ans2 = countSwap(s);

	    if (ans1 > ans2)
	        System.out.println(ans1);
	    else
	        System.out.println(ans2);
    }
}

Python Implementation:

def CountSwap(s, n):
	s = list(s)

	count = 0
	ans = True
	for i in range(n // 2):
		left = i

		right = n - left - 1

		while left < right:
			if s[left] == s[right]:
				break
			else:
				right -= 1

		if left == right:
			ans = False
			break
		else:
			for j in range(right, n - left - 1):
				(s[j], s[j + 1]) = (s[j + 1], s[j])
				count += 1
	if ans:
		return (count)
	else:
		return -1


s = 'aabb'
n = len(s)

ans1 = CountSwap(s, n)
ans2 = CountSwap(s[::-1], n)
print(max(ans1, ans2))

Time complexity: Since we are running two nested loops on the length of string, the time complexity is O(n^2)

Space complexity: Since we aren’t using any extra space, Therefore Auxiliary space used is O(1).

Make a Career in Data Science & AI in Few Months

With this article at Logicmojo, you must have the complete idea of solving Minimum Swaps To Make Palindrome problem.

Advanced Data Structures Algorithms & System Design(HLD+LLD) by Logicmojo

Minimum Swaps To Make Palindrome

𝑻𝒂𝒃𝒍𝒆 𝒐𝒇 𝑪𝒐𝒏𝒕𝒆𝒏𝒕

Problem Statement: Minimum Swaps To Make Palindrome

Two Pointer Approach

Advanced
Data Structures Algorithms & System Design(HLD+LLD)
by Logicmojo