Missing Number

Problem Statement: Missing Number

You are given a list of n-1 integers, all of which are between 1 and n. The list contains no duplicates. In the list, one of the integers is missing. To find the missing integer, write an efficient code.

Examples:

Input: list[] = {8, 3, 9, 6, 3, 7, 4,10,1}
Output: 5
Explanation: The missing number from 1 to 10 is 5.

Input: list[] = {2, 3, 5, 1}
Output: 4
Explanation: The missing number from 1 to 5 is 4.

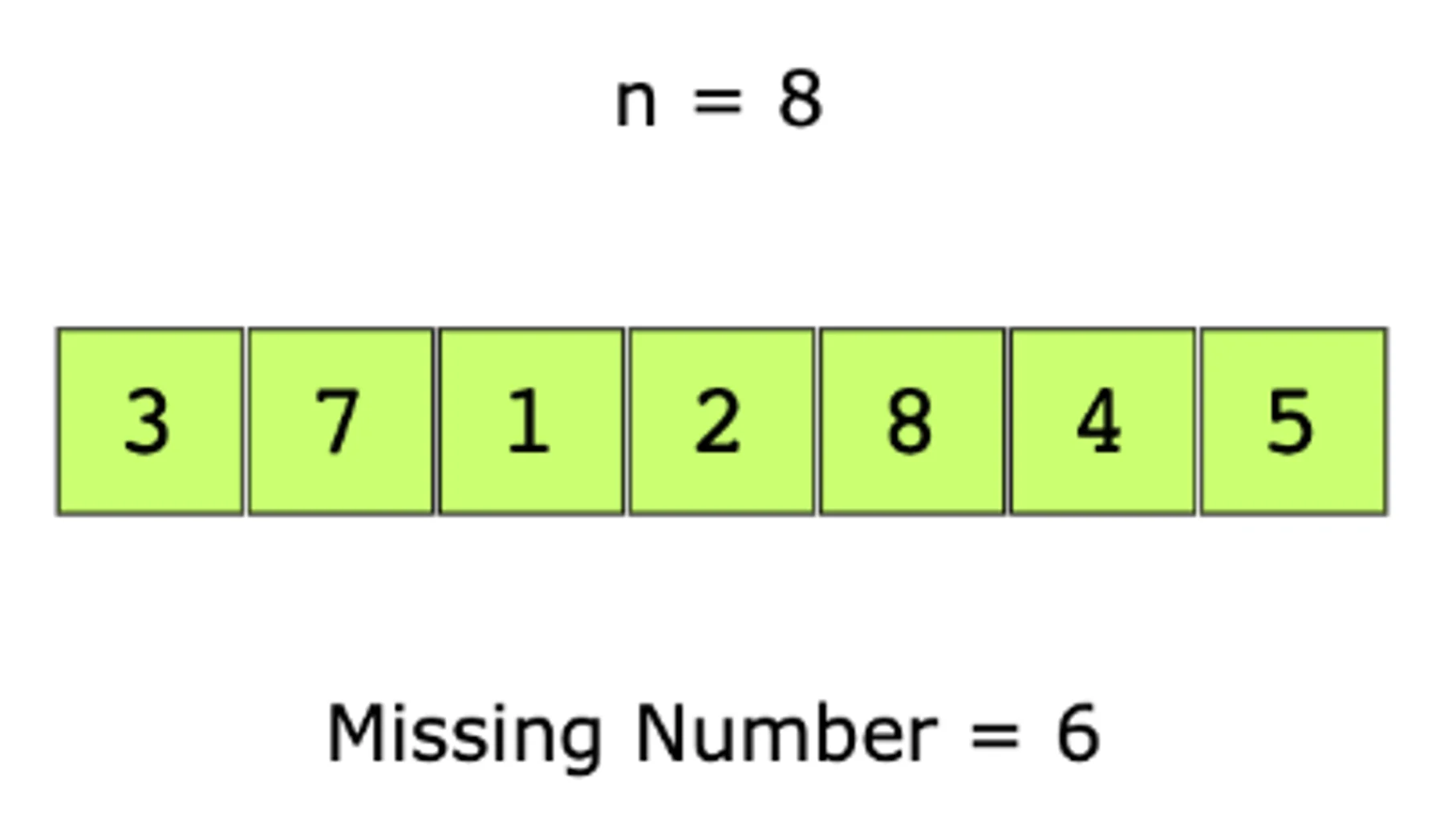
We have presented two approaches to find the two elements:

 • Simple Approach
 • XOR Approach

Simple Approach

A simple solution is to simply scan the input array for every integer between 1 and n, halting the search as soon as a missing number is found. The time complexity of the input array will be O(n^2) because it is not sorted.

Can you do better than O(n^2)? Yes.

You could sort the array and then perform a linear scan O(n) to discover the missing number by comparing all successive elements. However, because of the time spent sorting, the temporal complexity of this approach is O(n log n).

You can do better. Here is a linear, O(n), solution that uses the arithmetic series sum formula.

sum(n)= n*(n+1)/2

Algorithm:

1. Calculate the summation of first N natural numbers as Total = N * (N + 1) / 2

2. Create a variable sum to store the summation of elements of the array.

3. Iterate the array from start to end.

4. Updating the value of sum as sum = sum + array[i]

5. Print the missing number as the Total – sum


C++ Implementation:



#include <bits/stdc++.h>
using namespace std;
int getMissingNo(int a[], int n)
{

	int total = (n + 1) * (n + 2) / 2;
	for (int i = 0; i < n; i++)
		total -= a[i];
	return total;
}
int main()
{
	int arr[] = { 1, 2, 4, 5, 6 };
	int n = sizeof(arr) / sizeof(arr[0]);
	int miss = getMissingNo(arr, n);
	cout << miss;
}



Java Implementation:



import java.util.*;
import java.util.Arrays;
class Main{
	public static int findMissingNumbers(int[] nums)
	{
		int n=nums.length;
		int sum=((n+1)*(n+2))/2;
		for(int i=0;i<n;i++)
		sum-=nums[i];
		return sum;
	}
	public static void main(String[] args)
	{
		int[] a = { 1, 2, 4, 5, 6 };
		System.out.println(findMissingNumbers(a));
	}
}



Python Implementation:



def getMissingNo(A):
	n = len(A)
	total = (n + 1)*(n + 2)/2
	sum_of_A = sum(A)
	return total - sum_of_A

A = [1, 2, 4, 5, 6]
miss = getMissingNo(A)
print(miss)





Time Complexity: O(n).
Only one traversal of the array is needed.
Space Complexity: O(1).
No extra space is needed





XOR Approach

We know that XOR of two equal numbers cancels each other. We can take advantage of this fact to find the missing number in the limited range array.

The idea is to compute XOR of all the elements in the array and compute XOR of all the elements from 1 to n+1, where n is the array’s size. Now the missing number would be the XOR between the two.

This approach is demonstrated below in C++, Java, and Python:

C++ Implementation:



#include <bits/stdc++.h>
using namespace std;


int getMissingNo(int a[], int n)
{
	int x1 = a[0];
	int x2 = 1;

	for (int i = 1; i < n; i++)
		x1 = x1 ^ a[i];

	for (int i = 2; i <= n + 1; i++)
		x2 = x2 ^ i;

	return (x1 ^ x2);
}

int main()
{
	int arr[] = { 1, 2, 4, 5, 6 };
	int n = sizeof(arr) / sizeof(arr[0]);
	int miss = getMissingNo(arr, n);
	cout << miss;
}



Java Implementation:



class Main
{
    
    public static int getMissingNumber(int[] arr)
    {
        int xor = 0;
        for (int i: arr) {
            xor = xor ^ i;
        }
 
        for (int i = 1; i <= arr.length + 1; i++) {
            xor = xor ^ i;
        }
 
        return xor;
    }
 
    public static void main(String[] args)
    {
        int[] arr = { 1, 2, 3, 4, 5, 7, 8, 9, 10 };
 
        System.out.println("The missing number is " + getMissingNumber(arr));
    }
}



Python Implementation:



def getMissingNumber(arr):
    xor = 0
    for i in arr:
        xor = xor ^ i
 
    for i in range(1, len(arr) + 2):
        xor = xor ^ i
 
    return xor
 
if __name__ == '__main__':
 
    arr = [1, 2, 3, 4, 5, 7, 8, 9, 10]
    print('The missing number is', getMissingNumber(arr))





Time Complexity: O(n).
Only one traversal of the array is needed.
Space Complexity: O(1).
No extra space is needed



With this article at Logicmojo, you must have the complete idea of solving Missing Number problem.