Next Greater Permutation

Problem Statement: Next Greater Permutation

Next Greater Permutation: Given an array Arr[] of integers, rearrange the numbers of the given array into the lexicographically next greater permutation of numbers.
If such an arrangement is not possible, it must rearrange it as the lowest possible order (i.e., sorted in ascending order).

Example:

Array: [1, 2, 3, 4]

Next Greater Permutation: [1, 2, 4, 3]

Next Greater Permutation: [1, 3, 2, 4]

Next Greater Permutation: [1, 3, 4, 2]

Next Greater Permutation: [1, 4, 2, 3]

Next Greater Permutation: [1, 4, 3, 2]

Next Greater Permutation: [2, 1, 3, 4]

Array: [4, 3, 2, 1]

Next Greater Permutation: [1, 2, 3, 4]

We have presented two approaches to find the two elements:

Naive Approach

The very first approach that you are gonna tell the interviewer is the brute so for this problem we simply need to find out every possible permutation of list formed by the elements of the given array and find out the permutation which is just larger than the given one. But this one will be a very naive approach, since it requires us to find out every possible permutation which will take really long time and the implementation is complex.

For finding, all possible permutations, it is taking N!xN. N represents the number of elements present in the input array. Also for searching input arrays from all possible permutations will take N!. Therefore, it has a Time complexity of O(N! x N).

Efficient

The following algorithm generates the next permutation lexicographically after a given permutation. It changes the given permutation in-place.

1. Find the largest index k such that a[k] < a[k + 1]. If no such index exists, the permutation is the last permutation.

2. Find the largest index l greater than k such that a[k] < a[l].

3. Swap the value of a[k] with that of a[l].

4. Reverse the sequence from a[k + 1] up to and including the final element a[n].

Let's visualise it through below image

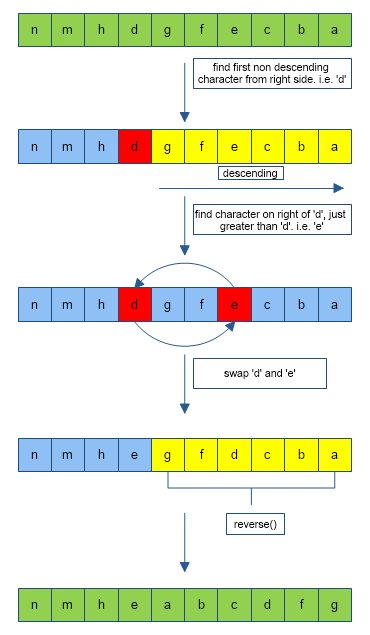
Time: O(N) where N is the number of elements in the input array.

Space: O(1)

class Solution {
public:
    void nextPermutation(vector<int>& nums) {
        int n = nums.size();
        if (n < 2) return;
        
        int i = n-1, j = n-1;
        
        // Find the largest index i such that nums[i] < nums[i + 1]:
        while (i > 0 && nums[i-1] >= nums[i]) i--;
        
        // If no such index exists - reverse the array and were done:
        if (i == 0) {
            reverse(nums.begin(), nums.end());
            return;
        }
        
        // Find the largest index j > i such that nums[i] < nums[j]:
        i--;
        while (j > i && nums[j] <= nums[i]) j--;
        
        // Swap nums[i] and nums[j]:
        swap(nums[i], nums[j]);
        
        // Reverse the array from index i until the end:
        reverse(nums.begin() + i + 1, nums.end());
    }
};

class Solution:
    def nextPermutation(self, nums):
        left = len(nums) - 2
        
        while left >= 0 and nums[left + 1] <= nums[left]:
            left -= 1
            
        if left >= 0:
            right = len(nums) - 1
            while nums[right] <= nums[left]:
                right -= 1
            self.swap(nums, right, left)
            
        self.reverse(nums, left + 1)
        
        return
    
    def swap(self,nums, right, left):
        nums[right], nums[left] = nums[left], nums[right]
        
    def reverse(self, nums, right):
        left = len(nums) - 1
        while right < left:
            self.swap(nums, right, left)
            right += 1
            left -= 1
ob1 = Solution()
print(ob1.nextPermutation([4,3,2,1]))