Pascal's Triangle

Problem Statement: Pascal's Triangle

In this triangle, the value at a position is equal to the sum of values of the 2 elements just above it.

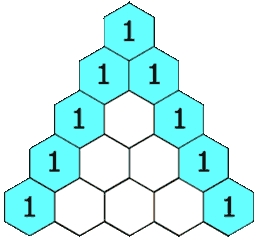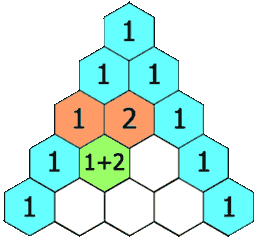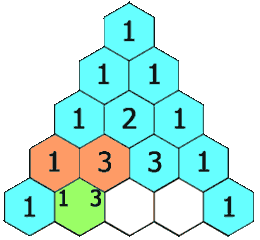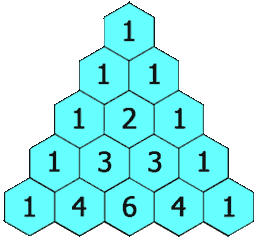
Examples

The 2nd element of 5th row is 1+3 => 4

The 3rd element of 5th row is 3+3 => 6

The 4th element of 5th row is 3+1 => 4

Given a number n, find the first n row of pascal's triangle.

Solution

Intuition: When you see the image above, you get a pretty good idea of what you are supposed to do here. Think about the image as a matrix now where each line is basically a row in the matrix. So, first things first, if you are at the edge of the matrix, the value is 1, that's for sure. Now, what about the inner elements? Well, any inner element is obtained by doing the sum of the 2 values present in the row just above it, i.e., if the element is at index (i, j), then matrix[i][j] can be obtained by doing matrix[i - 1][j - 1] + matrix[i - 1][j].

Approach

To solve the problem, we need to first create an array of size N or numRows (input value). This array is used to store each of the rows expected in the output, so, for example, array[1] = [1,1]. In this array, the number of columns (say, numCols) is equal to the number of the i-th row + 1 (Since, 0-indexed), i.e., for 0-th row, numCols = 1. So, the number of columns is different for each row.

Next, we need to run a loop from i = 0 to numRows - 1 (inclusive) in order to store each row in our array. For each of iteration of this loop, we follow the below steps:

1. Create an array of size (i + 1) (For some languages such as C++, you need to create a 2D array at the start of the program and resize array[i] to (i + 1)).

2. Set the first and last value of array[i] to 1.

3. Run another loop from j = 1 to i - 1 (inclusive) and for each iteration put array[i][j] = array[i - 1][j - 1] + array[i - 1][j].

After iterating numRows times, you return the array.

class Solution {
public:
    vector<vector<int>> generate(int numRows) {
        vector<vector<int>> r(numRows);

        for (int i = 0; i < numRows; i++) {
            r[i].resize(i + 1);
            r[i][0] = r[i][i] = 1;
  
            for (int j = 1; j < i; j++)
                r[i][j] = r[i - 1][j - 1] + r[i - 1][j];
        }
        
        return r;
    }
};

class Solution:
    def generate(self, numRows):
        triangles = []
        for i in range(numRows):
            triangles.append([])
            for j in range(i + 1):
                if j == 0 or j == i:
                    triangles[i].append(1)
                else:
                    triangles[i].append(triangles[i - 1][j - 1] + triangles[i - 1][j])
        return triangles
ob1 = Solution()
print(ob1.generate(5))

Time Complexity: O(numRows²)

Sapce Complexity: O(numRows²)