We have this concept in computer science as well. Take the example of a printer. Suppose we have a shared printer, and several jobs are to be printed at once. The printer maintains a printing "queue" internally, and prints the jobs in sequence based on which came first.

Another instance where queues are extensively used is in the operating system of our machines. An OS maintains several queues such as a job queue, a ready queue, and a device queue for each of the processes.

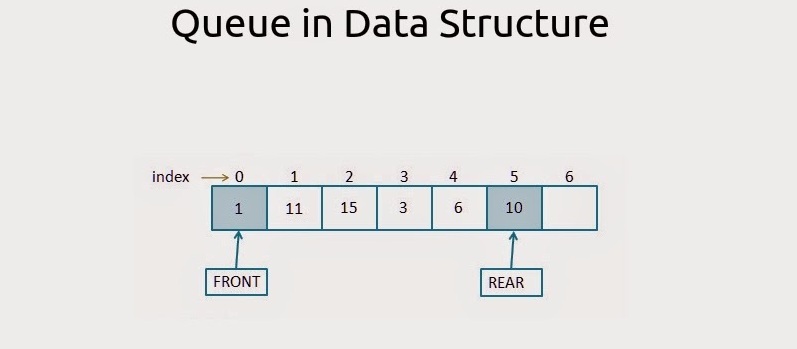
Queue is also an abstract data type or a linear data structure, just like stack data structure, in which the first element is inserted from one end called the REAR(also called tail), and the removal of existing element takes place from the other end called as FRONT(also called head).

Advantages

 • Helps to manage data in FIFO (First In First Out) order
 • Can handle items of any data type which makes it extremely flexible

Disadvantages

 • Adding or deleting elements from the middle is complex

Applications of Queue

Queue, as the name suggests is used whenever we need to manage any group of objects in an order in which the first one coming in, also gets out first while the others wait for their turn, like in the following scenarios:

1. Serving requests on a single shared resource, like a printer, CPU task scheduling etc.

2. In real life scenario, Call Center phone systems uses Queues to hold people calling them in an order, until a service representative is free.

3. Handling of interrupts in real-time systems. The interrupts are handled in the same order as they arrive i.e First come first served.

Basic Operations of Queue

A queue is an object (an abstract data structure - ADT) that allows the following operations:
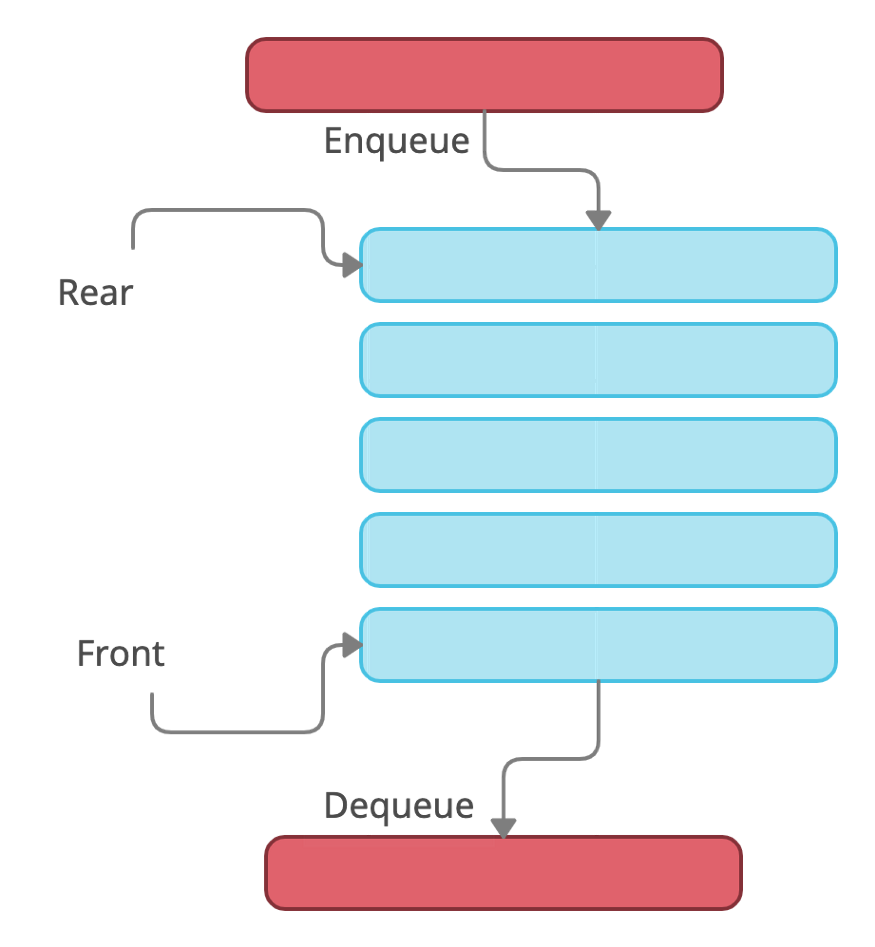
Enqueue: Add an element to the end of the queue
Dequeue: Remove an element from the front of the queue
IsEmpty: Check if the queue is empty
IsFull: Check if the queue is full
Peek: Get the value of the front of the queue without removing it

Algorithm for ENQUEUE operation

1. Check if the queue is full or not.
2. If the queue is full, then print overflow error and exit the program.
3. If the queue is not full, then increment the tail and add the element.

Algorithm for DEQUEUE operation

1. Check if the queue is empty or not.
2. If the queue is empty, then print underflow error and exit the program.
3. If the queue is not empty, then print the element at the head and increment the head.

Implementation in Python

# Queue implementation in Python

class Queue:

    def __init__(self):
        self.queue = []

    # Add an element
    def enqueue(self, item):
        self.queue.append(item)

    # Remove an element
    def dequeue(self):
        if len(self.queue) < 1:
            return None
        return self.queue.pop(0)

    # Display  the queue
    def display(self):
        print(self.queue)

    def size(self):
        return len(self.queue)


q = Queue()
q.enqueue(1)
q.enqueue(2)
q.enqueue(3)
q.enqueue(4)
q.enqueue(5)

q.display()

q.dequeue()

print("After removing an element")
q.display()

Implementation in C++

// Queue implementation in C++

#include <iostream>
#define SIZE 5

using namespace std;

class Queue {
   private:
  int items[SIZE], front, rear;

   public:
  Queue() {
    front = -1;
    rear = -1;
  }

  bool isFull() {
    if (front == 0 && rear == SIZE - 1) {
      return true;
    }
    return false;
  }

  bool isEmpty() {
    if (front == -1)
      return true;
    else
      return false;
  }

  void enQueue(int element) {
    if (isFull()) {
      cout << "Queue is full";
    } else {
      if (front == -1) front = 0;
      rear++;
      items[rear] = element;
      cout << endl
         << "Inserted " << element << endl;
    }
  }

  int deQueue() {
    int element;
    if (isEmpty()) {
      cout << "Queue is empty" << endl;
      return (-1);
    } else {
      element = items[front];
      if (front >= rear) {
        front = -1;
        rear = -1;
      } /* Q has only one element, so we reset the queue after deleting it. */
      else {
        front++;
      }
      cout << endl
         << "Deleted -> " << element << endl;
      return (element);
    }
  }

  void display() {
    /* Function to display elements of Queue */
    int i;
    if (isEmpty()) {
      cout << endl
         << "Empty Queue" << endl;
    } else {
      cout << endl
         << "Front index-> " << front;
      cout << endl
         << "Items -> ";
      for (i = front; i <= rear; i++)
        cout << items[i] << "  ";
      cout << endl
         << "Rear index-> " << rear << endl;
    }
  }
};

int main() {
  Queue q;

  //deQueue is not possible on empty queue
  q.deQueue();

  //enQueue 5 elements
  q.enQueue(1);
  q.enQueue(2);
  q.enQueue(3);
  q.enQueue(4);
  q.enQueue(5);

  // 6th element can't be added to because the queue is full
  q.enQueue(6);

  q.display();

  //deQueue removes element entered first i.e. 1
  q.deQueue();

  //Now we have just 4 elements
  q.display();

  return 0;
}

Limitations of Queue

The main limitation of queues in a data structure is one of the basic operations of deleting an element from it is cumbersome. By the definition of a queue, when we add an element in Queue, the rear pointer is increased by 1 whereas, when we remove an element front pointer is increased by 1. But an array implementation of queue this may cause the problem as follows:

Consider operations performed on a Queue (with SIZE = 5) as follows:

Initially empty Queue is there so,front = 0 and rear = -1

When we add 5 elements to queue, the state of the queue becomes as follows with front = 0 and rear = 4
10
20
30
40
50

Now suppose we delete 2 elements from Queue then, the state of the Queue becomes as follows, with front = 2 and rear = 4

30
40
50
Now, actually we have deleted 2 elements from the queue so, there should be space for another 2 elements in the queue, but as the rear pointer is pointing at last position and Queue overflow condition(Rear == SIZE-1) is true, we can’t insert the new element in the queue even if it has an empty space. To overcome this problem there is another variation of queue called CIRCULAR QUEUE.

Time & Space Complexity Analysis

We know exactly, on which position new element will be added and from where an element will be removed, hence both these operations requires a single step.
Enqueue: O(1)
Dequeue: O(1)
Size: O(1)

With this article at Logicmojo, you must have the complete idea of analyzing Queue Data Structure.

Good Luck & Happy Learning!!