Quicksort is one of the efficient and most commonly used algorithms. Most of the languages used quicksort in their inbuild “sort” method implementations. The name comes from the fact that it sorts data faster than any commonly available sorting algorithm and like Merge sort, it also follows the divide and conquer principle.

Quicksort, in particular, is an interesting one nevertheless it takes enough time to get your head around it. Quicksort breaks down the problem of sorting the complete array into smaller problems by breaking down the array into smaller subarray. This technique of splitting the bigger problem into smaller problems is called divide and conquer approach.

Quick Sort Idea — Divide and Conquer

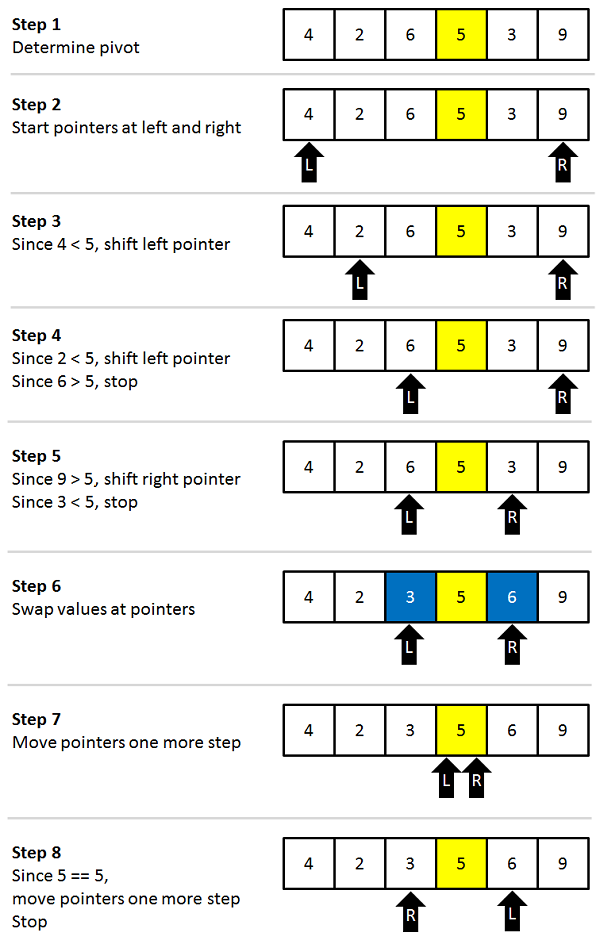
Divide part — Divide the problem into two smaller sub-problems by partition the array X[l…r] into two smaller subarrays around some pivot value in the array. Partition algorithm returns the pivotIndex (index of the pivot in the sorted array) after the partition.

Left Subproblem — Sorting array X[] from l to pivotIndex -1

Right Subproblem— Sorting array X[] from pivotIndex +1 to r

Conquer Part — Now, we solve both the sub-problems or sort both the smaller arrays recursively. We need not worry about the solutions to the sub-problems because recursion will do the rest of the work for us.

Combine Part — There is no need to combine parts because after sorting both smaller arrays, our whole array will get sorted automatically. Why? Think.

Algorithm

Characteristics of Quicksort

The performance of quicksort is in order of nlogn for most of the cases. If the list of elements is already in sorted order or nearly sorted order then it takes n² comparisons to sort the array.

Quicksort has a space complexity of O(logn) even in the worst case when it is carefully implemented such that

in-place partitioning is used. This requires O(1).

After partitioning, the partition with the fewest elements is (recursively) sorted first, requiring at most O(logn) space. Then the other partition is sorted using tail-recursion or iteration.

In-place algorithm: As we have seen above the Quicksort practically needs more than constant O(1) space. It needs memory in order of O(log n) this completely disqualifies quicksort as an in-place algorithm. However, quicksort is always considered to be in-place, it sorts the elements within the array with at most a constant amount of them outside the array at any given time.

Unstable: Quicksort has one bigger difference with merge sort, and this ends up being a key point between these otherwise similar algorithms. This is the fact that quicksort is an unstable algorithm, meaning that it won’t be guaranteed to preserve the order of elements as it reorders; two elements that are exactly the same in the unsorted array could show up in a reversed order in the sorted one! Stability ends up being what causes people to choose merge sort over quicksort, and it’s the one area where merge sort appears as the obvious winner.

Applications of Quick Sort

Before diving into any algorithm, its very much necessary for us to understand what are the real world applications of it. Quick sort provides a fast and methodical approach to sort any lists of things. Following are some of the applications where quick sort is used.

Commercial computing: Used in various government and private organizations for the purpose of sorting various data like sorting of accounts/profiles by name or any given ID, sorting transactions by time or locations, sorting files by name or date of creation etc.

Numerical computations: Most of the efficiently developed algorithms use priority queues and inturn sorting to achieve accuracy in all the calculations.

Information search: Sorting algorithms aid in better search of information and what faster way exists than to achieve sorting using quick sort.

Implementation in Python

# Quick sort in Python

# function to find the partition position
def partition(array, low, high):

  # choose the rightmost element as pivot
  pivot = array[high]

  # pointer for greater element
  i = low - 1

  # traverse through all elements
  # compare each element with pivot
  for j in range(low, high):
    if array[j] <= pivot:
      # if element smaller than pivot is found
      # swap it with the greater element pointed by i
      i = i + 1

      # swapping element at i with element at j
      (array[i], array[j]) = (array[j], array[i])

  # swap the pivot element with the greater element specified by i
  (array[i + 1], array[high]) = (array[high], array[i + 1])

  # return the position from where partition is done
  return i + 1

# function to perform quicksort
def quickSort(array, low, high):
  if low < high:

    # find pivot element such that
    # element smaller than pivot are on the left
    # element greater than pivot are on the right
    pi = partition(array, low, high)

    # recursive call on the left of pivot
    quickSort(array, low, pi - 1)

    # recursive call on the right of pivot
    quickSort(array, pi + 1, high)


data = [8, 7, 2, 1, 0, 9, 6]
print("Unsorted Array")
print(data)

size = len(data)

quickSort(data, 0, size - 1)

print('Sorted Array in Ascending Order:')
print(data)

Implementation in C++

// Quick sort in C++

#include <iostream>
using namespace std;

// function to swap elements
void swap(int *a, int *b) {
  int t = *a;
  *a = *b;
  *b = t;
}

// function to print the array
void printArray(int array[], int size) {
  int i;
  for (i = 0; i < size; i++)
    cout << array[i] << " ";
  cout << endl;
}

// function to rearrange array (find the partition point)
int partition(int array[], int low, int high) {
    
  // select the rightmost element as pivot
  int pivot = array[high];
  
  // pointer for greater element
  int i = (low - 1);

  // traverse each element of the array
  // compare them with the pivot
  for (int j = low; j < high; j++) {
    if (array[j] <= pivot) {
        
      // if element smaller than pivot is found
      // swap it with the greater element pointed by i
      i++;
      
      // swap element at i with element at j
      swap(&array[i], &array[j]);
    }
  }
  
  // swap pivot with the greater element at i
  swap(&array[i + 1], &array[high]);
  
  // return the partition point
  return (i + 1);
}

void quickSort(int array[], int low, int high) {
  if (low < high) {
      
    // find the pivot element such that
    // elements smaller than pivot are on left of pivot
    // elements greater than pivot are on righ of pivot
    int pi = partition(array, low, high);

    // recursive call on the left of pivot
    quickSort(array, low, pi - 1);

    // recursive call on the right of pivot
    quickSort(array, pi + 1, high);
  }
}

// Driver code
int main() {
  int data[] = {8, 7, 6, 1, 0, 9, 2};
  int n = sizeof(data) / sizeof(data[0]);
  
  cout << "Unsorted Array: \n";
  printArray(data, n);
  
  // perform quicksort on data
  quickSort(data, 0, n - 1);
  
  cout << "Sorted array in ascending order: \n";
  printArray(data, n);
}

Time & Space Complexity Analysis

Worst Case Complexity [Big-O]: O(n2)
It occurs when the pivot element picked is either the greatest or the smallest element. This condition leads to the case in which the pivot element lies in an extreme end of the sorted array. One sub-array is always empty and another sub-array contains n - 1 elements. Thus, quicksort is called only on this sub-array. However, the quicksort algorithm has better performance for scattered pivots.

Best Case Complexity [Big-omega]: O(n*log n)
It occurs when the pivot element is always the middle element or near to the middle element.

Average Case Complexity [Big-theta]: O(n*log n)
It occurs when the above conditions do not occur.

Space Complexity: The space complexity for quicksort is O(log n).

With this article at Logicmojo, you must have the complete idea of analyzing Quick Sort algorithm.

Good Luck & Happy Learning!!