Rat In A Maze

Back to home

𝑻𝒂𝒃𝒍𝒆 𝒐𝒇 𝑪𝒐𝒏𝒕𝒆𝒏𝒕

Problem Statement: Rat In A Maze
Approach: Backtracking

Logicmojo - Updated Jan 2, 2023

Problem Statement: Rat In A Maze

You are given a maze in the form of a matrix of size n * m. Each cell is either clear or blocked denoted by 1 and 0 respectively. A rat sits at the top-left cell and there exists a block of cheese at the bottom-right cell. Both these cells are guaranteed to be clear. You need to find if the rat can get the cheese if it can move only in one of the two directions - down and right. It can’t move to blocked cells.

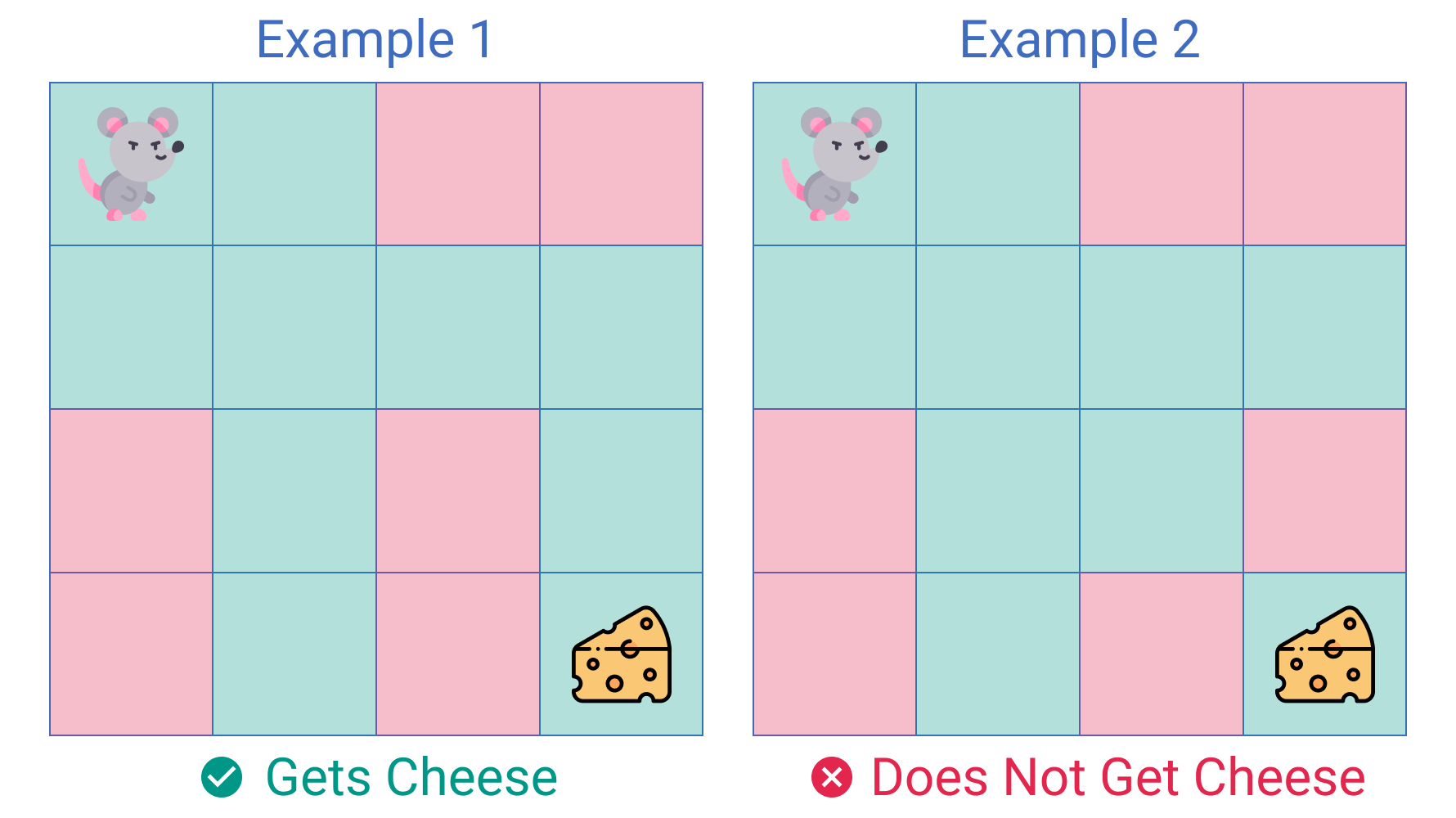
Approach: Backtracking

Backtracking is an algorithmic-technique for solving problems recursively by trying to build a solution incrementally. Solving one piece at a time, and removing those solutions that fail to satisfy the constraints of the problem at any point of time (by time, here, is referred to the time elapsed till reaching any level of the search tree) is the process of backtracking.

Learn More️

Form a recursive function, which will follow a path and check if the path reaches the destination or not. If the path does not reach the destination then backtrack and try other paths.

Algorithm:

1. Firstly, create a matrix to store your solution. It should contain all zeros and should be of the same size as the maze matrix.

2. Make a recursive call with the position of the rat in the matrix: initial maze matrix, solution matrix

3. If the position provided is invalid, return from the function.

4. Otherwise, mark the position as 1 in the solution matrix.

5. Recursively call for position (i+1, j), (i, j+1), (i-1, j), and (i, j-1).

C++ Implementation:

/* C/C++ program to solve Rat in a Maze problem using 
   backtracking */
#include<stdio.h> 
  
// Maze size 
#define N 4  
  
bool solveMazeUtil(int maze[N][N], int x, int y, int sol[N][N]); 
  
/* A utility function to print solution matrix sol[N][N] */
void printSolution(int sol[N][N]) 
{ 
    for (int i = 0; i < N; i++) 
    { 
        for (int j = 0; j < N; j++) 
            printf(" %d ", sol[i][j]); 
        printf(""); 
    } 
} 
  
/* A utility function to check if x,y is valid index for N*N maze */
bool isSafe(int maze[N][N], int x, int y) 
{ 
    // if (x,y outside maze) return false 
    if(x >= 0 && x < N && y >= 0 && y < N && maze[x][y] == 1) 
        return true; 
  
    return false; 
} 
  

bool solveMaze(int maze[N][N]) 
{ 
    int sol[N][N] = { {0, 0, 0, 0}, 
        {0, 0, 0, 0}, 
        {0, 0, 0, 0}, 
        {0, 0, 0, 0} 
    }; 
  
    if(solveMazeUtil(maze, 0, 0, sol) == false) 
    { 
        printf("Solution doesn't exist"); 
        return false; 
    } 
  
    printSolution(sol); 
    return true; 
} 
  

bool solveMazeUtil(int maze[N][N], int x, int y, int sol[N][N]) 
{ 
    // if (x,y is goal) return true 
    if(x == N-1 && y == N-1) 
    { 
        sol[x][y] = 1; 
        return true; 
    } 
  
    // Check if maze[x][y] is valid 
    if(isSafe(maze, x, y) == true) 
    { 
        // mark x,y as part of solution path 
        sol[x][y] = 1; 
  
        /* Move forward in x direction */
        if (solveMazeUtil(maze, x+1, y, sol) == true) 
            return true; 
  
        /* If moving in x direction doesn't give solution then 
           Move down in y direction  */
        if (solveMazeUtil(maze, x, y+1, sol) == true) 
            return true; 
  
        /* If none of the above movements work then BACKTRACK:  
            unmark x,y as part of solution path */
        sol[x][y] = 0; 
        return false; 
    }    
  
    return false; 
} 
  
// driver program to test above function 
int main() 
{ 
    int maze[N][N]  =  { {1, 0, 0, 0}, 
        {1, 1, 0, 1}, 
        {0, 1, 0, 0}, 
        {1, 1, 1, 1} 
    }; 
  
    solveMaze(maze); 
    return 0; 
} 

        Try it Yourself

Python Implementation:

def valid_path(maze, i, j, m, n):
    if i == m or j == n:
        return False
    if maze[i][j] == 1:
        return False
    return True

def rat_maze(maze, i, j, m, n, arr):
    if arr[-1][-1] == 1:
        return True
    if valid_path(maze, i, j, m, n):
        arr[i][j] = 1
        if rat_maze(maze, i + 1, j, m, n, arr):
            return True
        if rat_maze(maze, i, j + 1, m, n, arr):
            return True
        arr[i][j] = 0
    return False

maze = [[0, 1, 0, 1, 1],
        [0, 0, 0, 0, 0],
        [1, 0, 1, 0, 1],
        [0, 0, 1, 0, 0],
        [1, 0, 0, 1, 0]]
arr = [[0 for i in range(len(maze[0]))] for j in range(len(maze))]
rat_maze(maze, 0, 0, len(maze), len(maze[0]), arr)
for i in arr:
    print(i)

        Try it Yourself

Time-Complexity: O(2^(n^2)). The recursion can run upper-bound 2^(n^2) times.

Auxiliary Space: O(n^2). Output matrix is required so an extra space of size n*n is needed.

With this article at Logicmojo, you must have the complete idea of solving Rat In A Maze problem.