 Logicmojo - Updated Jan 3, 2022
Logicmojo - Updated Jan 3, 2022
Problem Statement: Rotting Apples
You are given an n * m grid where each position can contain one of the three values:
Every day, all fresh apples which are adjacent to any rotten apple become rotten. Two cells are adjacent if they have a common edge, i.e., each cell can have upto four adjacent cells.
Find the minimum number of days required for all the apples to be rotten. If this is not possible return -1.
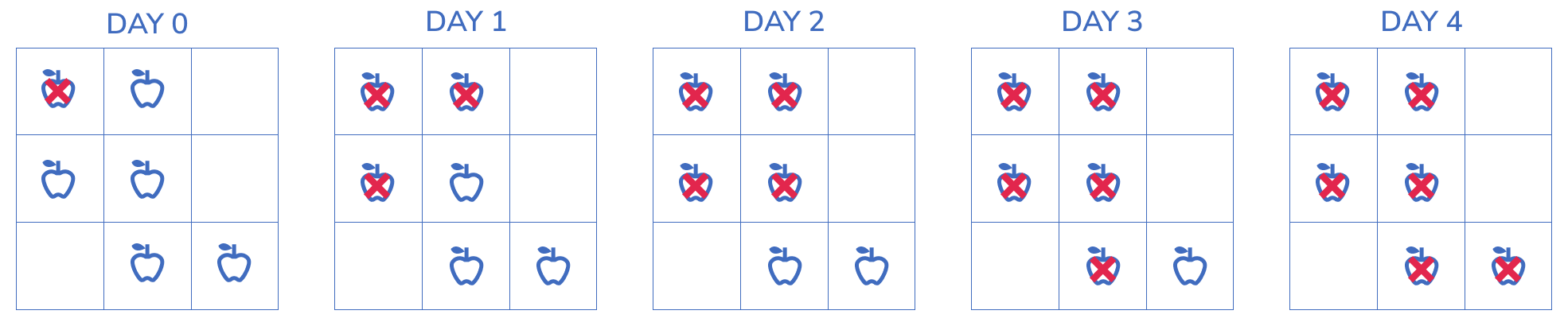
Example: matrix = [[2,1,1],[1,1,0],[0,1,1]]
Output: 4
Approach 1: Brute Force
The idea is very naive. Traverse through all apples in multiple rounds. In every round, rot the apples to the adjacent position of apples which were rotten in the last round. Time complexity is O((r*c)*(r*c)), i.e. matrix needs to be traversed again and again until there is no change in the matrix. This is not an efficient solution so we need to optimise it.
Approach 2: Using BFS
To find the total time required to rot all the apples we can do a breadth-first search(BFS) by assuming all the rotten apples as the starting point of the BFS.
Algorithm:
1. Create a queue of coordinates, to store the coordinates of required cells, that is, the queue should store the data of the form (row, col). Initialize a variable time as 0.
2. Traverse in the given matrix and add the coordinates of all the rotten apples to the queue.
3. While the queue is not empty repeat step 4.
4. Initialize a variable size as the size of the queue. Run a loop for i equals 0 to size(not included), and at every iteration pop out an element from the queue. If there is a fresh apples on its adjacent sides(left, right, top and bottom), push the coordinates of that apples to the queue and mark that apples as rotten. If there were some fresh apples then increment the time by 1 unit.
5. Now check if there is some fresh apples still present in the matrix, if yes, all the apples can not be rotten so return -1, else return time.
C++ Implementation:
#include<bits/stdc++.h> using namespace std; int applesRotting(vector<vector<int>>& grid) { if(grid.empty()) return 0; int m = grid.size(), n = grid[0].size(), days = 0, tot = 0, cnt = 0; queue<pair<int, int>> rotten; for(int i = 0; i < m; ++i){ for(int j = 0; j < n; ++j){ if(grid[i][j] != 0) tot++; if(grid[i][j] == 2) rotten.push({i, j}); } } int dx[4] = {0, 0, 1, -1}; int dy[4] = {1, -1, 0, 0}; while(!rotten.empty()){ int k = rotten.size(); cnt += k; while(k--){ int x = rotten.front().first, y = rotten.front().second; rotten.pop(); for(int i = 0; i < 4; ++i){ int nx = x + dx[i], ny = y + dy[i]; if(nx < 0 || ny < 0 || nx >= m || ny >= n || grid[nx][ny] != 1) continue; grid[nx][ny] = 2; rotten.push({nx, ny}); } } if(!rotten.empty()) days++; } return tot == cnt ? days : -1; } int main() { vector<vector<int>> v{ {2,1,1} , {1,1,0} , {0,1,1} } ; int rotting = applesRotting(v); cout<<"Minimum Number of Minutes Required "<<rotting<<endl; }
Python Implementation:
from collections import deque class Solution: def applesRotting(self, grid): queue = deque() X= [-1,1,0,0] Y = [0,0,1,-1] time = 0 m = len(grid) n = len(grid[0]) for i in range(len(grid)): for j in range(len(grid[0])): if grid[i][j] == 2: queue.append([i, j, time]) while queue: i, j , time = queue.popleft() for k in range(4): x, y = i + X[k], j + Y[k] if 0 <= x < m and 0 <= y < n and grid[x][y] == 1: grid[x][y] = 2 queue.append([x,y,time + 1]) for i in range(len(grid)): for j in range(len(grid[0])): if grid[i][j] == 1: return -1 return time ob1 = Solution() print(ob1.applesRotting([[2,1,1],[1,1,0],[0,1,1]]))
Time Complexity: O(r * c), because we have used breadth First Search which will traverse all the cells in the input matrix. Thus the time complexity is polynomial.
Space Complexity: O(r * c), using BFS takes this space. Because makes use of queue which stores the elements and thus this complexity.
With this article at Logicmojo, you must have the complete idea of solving Rotting Apples problem.