Search Rotated Sorted Array

Back to home

𝑻𝒂𝒃𝒍𝒆 𝒐𝒇 𝑪𝒐𝒏𝒕𝒆𝒏𝒕

Problem Statement: Search Rotated Sorted Array
Naive Approach
Efficient - Binary Search

Logicmojo - Updated Aug 28, 2021

Problem Statement: Search Rotated Sorted Array

Search for a given number in a sorted array, with unique elements, that has been rotated by some arbitrary number. Return -1 if the number does not exist.

arr[] = [5, 6, 7, 8, 9, 10, 1, 2, 3]

target = 3

Answer: At 8th index

We have presented two approaches to find the two elements:

• Naive Approach
• Efficient - Binary Search

Naive Approach

You can just return the index of the targeted value using linear search. But since it is not the optimised solution the interviewer will ask you to optimise it.

Approach 2: Efficient Using Binary Search

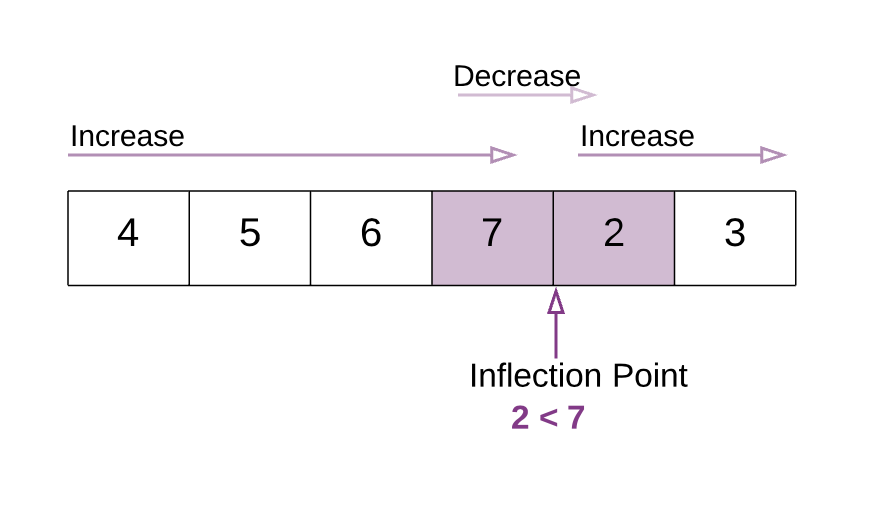
We have an ascending array, which is rotated at some pivot. Let's call the rotation the inflection point(IP)

One characteristic the inflection point holds is: arr[IP] > arr[IP + 1] and arr[IP] > arr[IP - 1]. So if we had an array like: [7, 8, 9, 0, 1, 2, 3, 4] the inflection point, IP would be the number 9.

We can perform a Binary Search. If A[mid] is bigger than A[left] we know the inflection point will be to the right of us, meaning values from a[left]...a[mid] are ascending.

So if target is between that range we just cut our search space to the left. Otherwise go right.

The other condition is that A[mid] is not bigger than A[left] meaning a[mid]...a[right] is ascending.

C++ Implementation:

int search(vector<int>& nums, int target) {
    int l = 0, r = nums.size()-1;
    while (l<=r) {
        int mid = (r-l)/2+l;
        if (nums[mid] == target)
            return mid;
        if (nums[mid] < nums[r]) {
            if (nums[mid]<target && target<=nums[r])
                l = mid+1;
            else
                r = mid-1;
        } else {
            if(nums[l]<=target && target<nums[mid])
                r = mid-1;
            else
                l = mid+1;
        }
    }
    return -1;
}

Python Implementation:

class Solution:
    def search(self, A, target):
        n = len(A)
        left, right = 0, n - 1
        if n == 0: return -1
        
        while left <= right:
            mid = left + (right - left) // 2
            if A[mid] == target: return mid
            
            # inflection point to the right. Left is strictly increasing
            if A[mid] >= A[left]:
                if A[left] <= target < A[mid]:
                    right = mid - 1
                else:
                    left = mid + 1
                    
            # inflection point to the left of me. Right is strictly increasing
            else:
                if A[mid] < target <= A[right]:
                    left = mid + 1
                else:
                    right = mid - 1
            
        return -1
ob1 = Solution()
print(ob1.search([5, 6, 7, 8, 9, 10, 1, 2, 3], 3))

Time Complexity:O(logn)

Space Complexity:O(1)

With this article at Logicmojo, you must have the complete idea of solving Search Rotated Sorted Array problem.