- What is Topological Sort
- Algorithm
- Implementation
- Time & Space Complexity Analysis
𝑻𝒂𝒃𝒍𝒆 𝒐𝒇 𝑪𝒐𝒏𝒕𝒆𝒏𝒕
 Logicmojo - Updated Sept 18, 2021
Logicmojo - Updated Sept 18, 2021
One of the difficulties in dealing with directed acyclic graphs (DAGs) is that they can look complicated and messy. This makes it difficult to see the relationships that vertices have with each other.
In this article, we’re going to discuss and learn how to rearrange the vertices of DAGs in such a way that will allow us to simplify these graphs and see possible patterns much easier.
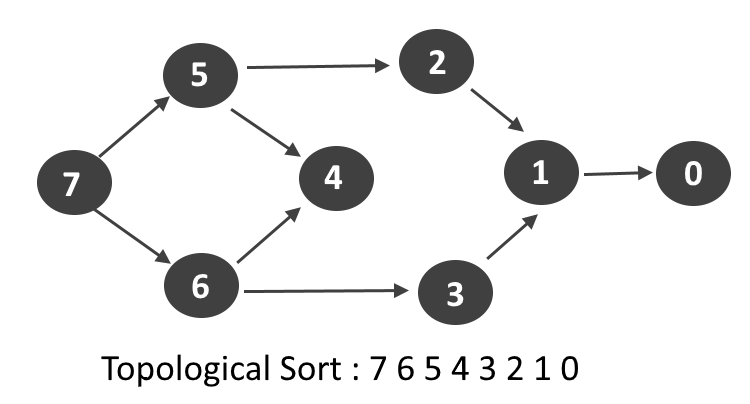
Topological sorting for Directed Acyclic Graph (DAG) is a linear ordering of vertices such that for every directed edge u v, vertex u comes before v in the ordering. Topological Sorting for a graph is not possible if the graph is not a DAG.
First remember that this algorithm only makes sense for directed graphs since it assumes a scheduling/ordering of the nodes (eg: direction of the edges).
You could technically use that same piece of code to traverse an undirected graph but it wouldn’t mean anything particular it's just a post order traversal
Algorithm
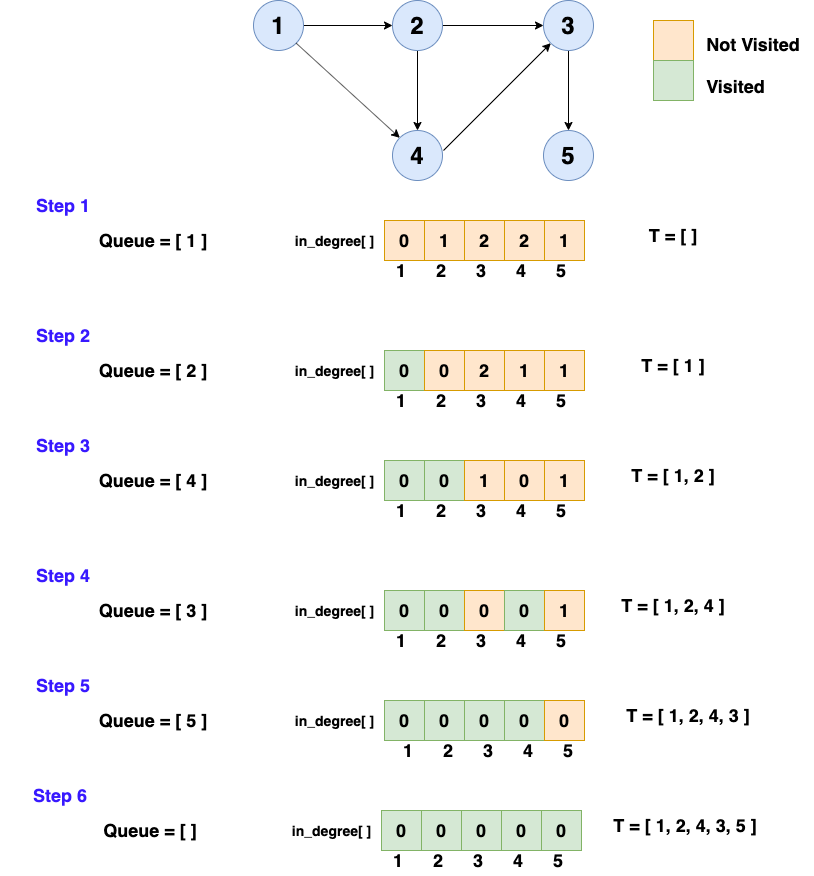
1. The algorithm of the topological sort goes like this:
2. Identify the node that has no in-degree(no incoming edges) and select that node as the source node of the graph
3. Delete the source node with zero in-degree and also delete all its outgoing edges from the graph. Insert the deleted vertex in the result array.
4. Update the in-degree of the adjacent nodes after deleting the outgoing edges
5. Repeat step 1 to step 3 until the graph is empty
Implementation in Python
def topological_sort(digraph): # digraph is a dictionary: # key: a node # value: a set of adjacent neighboring nodes # construct a dictionary mapping nodes to their # indegrees indegrees = {node : 0 for node in digraph} for node in digraph: for neighbor in digraph[node]: indegrees[neighbor] += 1 # track nodes with no incoming edges nodes_with_no_incoming_edges = [] for node in digraph: if indegrees[node] == 0: nodes_with_no_incoming_edges.append(node) # initially, no nodes in our ordering topological_ordering = [] # as long as there are nodes with no incoming edges # that can be added to the ordering while len(nodes_with_no_incoming_edges) > 0: # add one of those nodes to the ordering node = nodes_with_no_incoming_edges.pop() topological_ordering.append(node) # decrement the indegree of that node's neighbors for neighbor in digraph[node]: indegrees[neighbor] -= 1 if indegrees[neighbor] == 0: nodes_with_no_incoming_edges.append(neighbor) # we've run out of nodes with no incoming edges # did we add all the nodes or find a cycle? if len(topological_ordering) == len(digraph): return topological_ordering # got them all else: raise Exception("Graph has a cycle! No topological ordering exists.")
Implementation in C++
// A C++ program to print topological // sorting of a graph using indegrees. #include <bits/stdc++.h> using namespace std; // Class to represent a graph class Graph { // No. of vertices' int V; // Pointer to an array containing // adjacency listsList list<int>* adj; public: // Constructor Graph(int V); // Function to add an edge to graph void addEdge(int u, int v); // prints a Topological Sort of // the complete graph void topologicalSort(); }; Graph::Graph(int V) { this->V = V; adj = new list<int>[V]; } void Graph::addEdge(int u, int v) { adj[u].push_back(v); } // The function to do // Topological Sort. void Graph::topologicalSort() { // Create a vector to store // indegrees of all // vertices. Initialize all // indegrees as 0. vector<int> in_degree(V, 0); // Traverse adjacency lists // to fill indegrees of // vertices. This step // takes O(V+E) time for (int u = 0; u < V; u++) { list<int>::iterator itr; for (itr = adj[u].begin(); itr != adj[u].end(); itr++) in_degree[*itr]++; } // Create an queue and enqueue // all vertices with indegree 0 queue<int> q; for (int i = 0; i < V; i++) if (in_degree[i] == 0) q.push(i); // Initialize count of visited vertices int cnt = 0; // Create a vector to store // result (A topological // ordering of the vertices) vector<int> top_order; // One by one dequeue vertices // from queue and enqueue // adjacents if indegree of // adjacent becomes 0 while (!q.empty()) { // Extract front of queue // (or perform dequeue) // and add it to topological order int u = q.front(); q.pop(); top_order.push_back(u); // Iterate through all its // neighbouring nodes // of dequeued node u and // decrease their in-degree // by 1 list<int>::iterator itr; for (itr = adj[u].begin(); itr != adj[u].end(); itr++) // If in-degree becomes zero, // add it to queue if (--in_degree[*itr] == 0) q.push(*itr); cnt++; } // Check if there was a cycle if (cnt != V) { cout << "There exists a cycle in the graph\n"; return; } // Print topological order for (int i = 0; i < top_order.size(); i++) cout << top_order[i] << " "; cout << endl; } // Driver program to test above functions int main() { // Create a graph given in the // above diagram Graph g(6); g.addEdge(5, 2); g.addEdge(5, 0); g.addEdge(4, 0); g.addEdge(4, 1); g.addEdge(2, 3); g.addEdge(3, 1); cout << "Following is a Topological Sort of\n"; g.topologicalSort(); return 0; }
Time & Space Complexity Analysis
Breaking the algorithm into chunks, we:
Determine the indegree for each node. This is O(M) time (where M is the number of edges), since this involves looking at each directed edge in the graph once.
Find nodes with no incoming edges. This is a simple loop through all the nodes with some number of constant-time appends. O(N) time (where N is the number of nodes).
Add nodes until we run out of nodes with no incoming edges. This loop could run once for every node—O(N) times. In the body, we:
Do two constant-time operations on a vector to add a node to the topological ordering.
Decrement the indegree for each neighbor of the node we added. Over the entire algorithm, we'll end up doing exactly one decrement for each edge, making this step O(M)
time overall.
All together, the time complexity is O(M+N).
All in all, we have three structures and they're all O(N) space. Overall space complexity: O(N).
💡 Follow up: Try to do it using DFS
With this article at Logicmojo, you must have the complete idea of analyzing Topolgical Sort algorithm.
Good Luck & Happy Learning!!