Trapping Rain Water

Problem Statement: Trapping Rain Water

Given n non-negative integers representing an elevation map where the width of each bar is 1, compute how much water it is able to trap after raining.

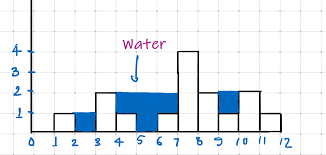
Example: arr = [0,1,0,2,1,0,1,3,2,1,2,1]

Output: 6

Explanation: The above elevation map (black section) is represented by array [0,1,0,2,1,0,1,3,2,1,2,1]. In this case, 6 units of rain water (blue section) are being trapped.

Crack your next tech interview with confidence!

We have presented two approaches to find the two elements:

Naive Approach

As per question for each element in the array, we find the maximum level of water it can trap after the rain, which is equal to the minimum of maximum height of bars on both the sides minus its own height. Time complexity will be O(n2)

So, it is not the optimised solution so we need to optimise it.

Approach 2: Efficient Using Left Right Array

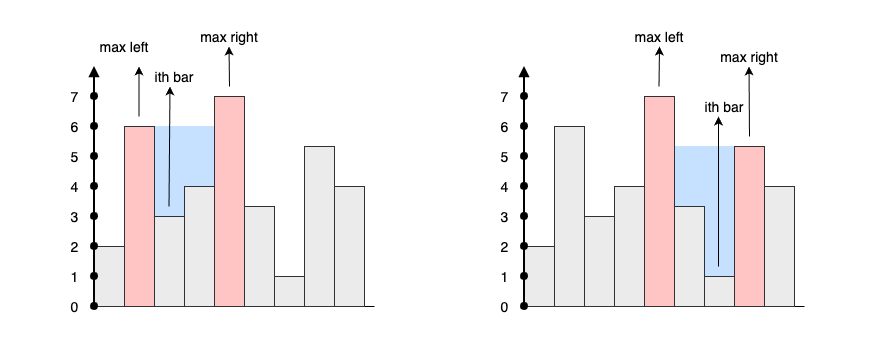
A ith bar can trap the water if and only if there exists a higher bar to the left and a higher bar to the right of ith bar.

To calculate how much amount of water the ith bar can trap, we need to look at the maximum height of the left bar and the maximum height of the right bar, then

1. The water level can be formed at ith bar is: waterLevel = min(maxLeft[i], maxRight[i])

2. If waterLevel >= height[i] then ith bar can trap waterLevel - height[i] amount of water.

class Solution { 
public:
    int trap(vector<int>& height) {
        int n = height.size();
        vector<int> leftMax(n), rightMax(n);
        for (int i = 1; i < n; ++i) 
            leftMax[i] = max(height[i-1], leftMax[i-1]);
        for (int i = n-2; i >= 0; --i) 
            rightMax[i] = max(height[i+1], rightMax[i+1]);
        
        int ans = 0;
        for (int i = 0; i < n; ++i) {
            int waterLevel = min(leftMax[i], rightMax[i]);
            if (waterLevel >= height[i]) ans += waterLevel - height[i];
        }
        return ans;
    }
};

class Solution:
    def trap(self, height):
        n = len(height)
        maxLeft, maxRight = [0] * n, [0] * n
        
        for i in range(1, n):
            maxLeft[i] = max(height[i-1], maxLeft[i-1])
        for i in range(n-2, -1, -1):
            maxRight[i] = max(height[i+1], maxRight[i+1])
            
        ans = 0
        for i in range(n):
            waterLevel = min(maxLeft[i], maxRight[i])
            if waterLevel >= height[i]:
                ans += waterLevel - height[i]
        return ans

ob1 = Solution()
print(ob1.trap([0,1,0,2,1,0,1,3,2,1,2,1]))

Time Complexity: O(N), where N is number of bars.

Space Complexity:O(N) since where are using left right array

💡 Follow up: To achieve in O(1) when looking at the maximum height of the bar on the left side and on the right side of ith bar, we pre-compute it