TWO SUM

Problem Statement: Two Sum

The problem statement is: We are given a list of N elements and a number M. We have to find two elements in the given list whose sum is M.

List = [a1, a2, ... , aN]
So, if the two elements are ai and aj, then:

a_i + a_j = M
Example:
Given numbers = [2, 7, 11, 15], target = 9,
Because nums[0] + nums[1] = 2 + 7 = 9,
return [0, 1]

We have presented two approaches to find the two elements:

Naive Approach

Here, we compare each and every number with the other in the list and see if they add up to the target number. If they do add up, we return their indices. Although this works, still it’s an inefficient solution, O(n²).

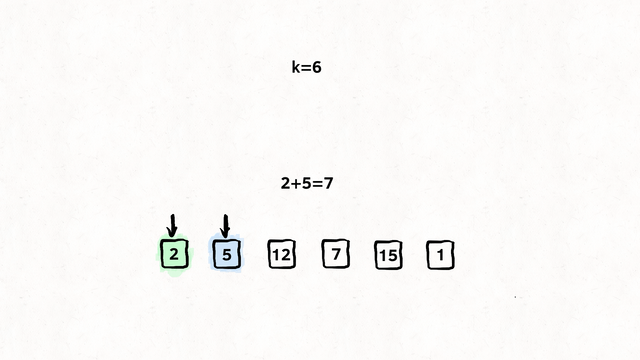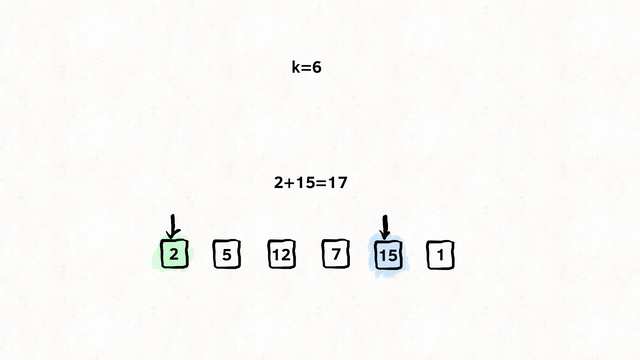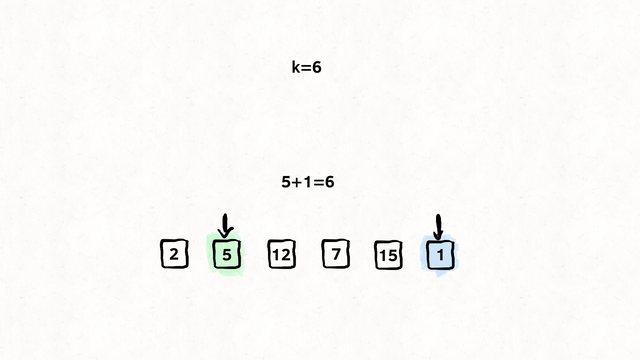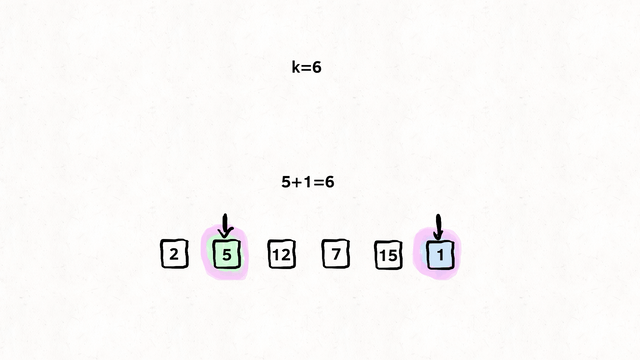
PseudoCode

Sort then Two Pointers

Since this problem require to output pair of indices instead of pair of values, so we need an array, let say arr to store their value with their respective indices. Sort array arr in increasing order by their values. Then use two pointer, left point to first element, right point to last element.

Time: O(N * logN), where N <= 10^4 is number of elements in the array nums.

Space: O(N)

vector<int> twoSum(vector<int>& nums, int target) {

    	vector<int> res,store;
    	store = nums;

    	sort(store.begin(), store.end());

    	int left=0,right=nums.size()-1;
    	int n1,n2;

    	while(left<right){
        	if(store[left]+store[right]==target){

            	n1 = store[left];
            	n2 = store[right];

            	break;

        	}
        	else if(store[left]+store[right]>target)
            	    right--;
        	else
            	    left++;
    	}

    	for(int i=0;i<nums.size();++i){

        	if(nums[i]==n1)
            	    res.emplace_back(i);
        	else if(nums[i]==n2)
            	    res.emplace_back(i);
    	}

    	    return res;
	}

    def twoSum(nums, target):
        arr = []
        for i, x in enumerate(nums):
            arr.append([x, i])
        arr.sort()  //Sort arr in increasing order by their values.
        
        left, right = 0, len(arr) - 1
        while left < right:
            sum2 = arr[left][0] + arr[right][0]
            if sum2 == target:
                return [arr[left][1], arr[right][1]]
            elif sum2 > target:
                right -= 1  //Try to decrease sum2
            else:
                left += 1  // Try to increase sum2

Optimal Approach using Hashmap

The idea is to store all elements in a Hashmap and then, traverse the list one by one. For each element ai, we will search for the element M - a[i] in the Hash Map which takes constant time O(1).

The steps are:

 • Store the list of N elements in a hash map
 • For a given element a[i], find the element M - a[i] in the Hash Map
 • Do the above step for each element in the list

Time Complexity: O(N)
Converting the list to a hashmap takes linear time. Search for a given element takes constant time O(1) but we have to do this for all N elements on average.

Space Complexity O(N)
The space requirement of a HashMap is the total number of elements to be inserted.

vector<int> twoSum(vector<int>& nums, int target) {

    vector<int> res;
    unordered_map<int, int> mp;

    for (int i = 0; i < nums.size(); ++i) {

   	 if (mp.find(target - nums[i]) != mp.end()) {

   		 res.emplace_back(i);
   		 res.emplace_back(mp[target - nums[i]]);
   		 return res;
   	 }

   	 mp[nums[i]] = i;
    }

    return res;
}

    def twoSum(nums, target)
        seen = {}
        for i, b in enumerate(nums):
            # a + b = target -> a = target - b
            a = target - b
            if a in seen:
                return [seen[a], i]
            seen[b] = i