Logicmojo - Jan 20, 2025
Logicmojo - Jan 20, 2025
Algorithms are at the very core of successful and efficient development. You’ll use them as you learn to code, you’ll be asked about them in technical interviews, and they’ll likely be part of your day-to-day development work.
Learning common algorithms individually is helpful, but what’s even better is getting used to algorithmic thinking. If you can train your brain to understand and follow algorithmic logic, writing your own algorithms will become much more intuitive. Algorithms and data structures are bugbears of the software development world

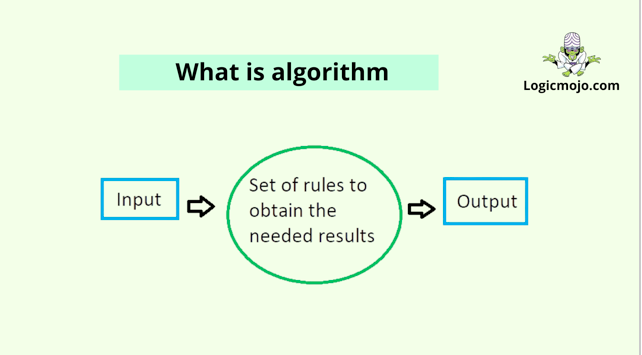
An algorithm is a finite set of instructions or logic that must be written in a specific order to complete a predetermined goal. An algorithm is not a complete programme or code; rather, it is the basic logic (solution) of a problem, which can be stated in a flowchart or as a high-level description in pseudocode.
Characteristics of Algorithm
To cook the recipe, one would not follow any written directions, but only the customary one. Similarly, not all written computer instructions are algorithms. There are some characteristics which every algorithm should follow.There are four different characteristics which deal with various aspects of algorithm.They are as follows:
🚀 Unambiguous (Input/Output Specified)
Algorithm should be clear and unambiguous. Each of its steps (or phases), and their inputs/outputs should be clear and must lead to only one meaning.
The input is the data to be transformed during the computation to produce the output. An algorithm should have 0 or more well-defined inputs. Input precision
requires that you know what kind of data, how much and what form the data should be.
The output is the data resulting from the computation (your intended result). An algorithm should have 1 or more well-defined outputs, and should match the desired output.
Output precision also requires that you know what kind of data, how much and what form the output should be (or even if there will be any output at all!).
🚀 Finiteness
The algorithm must terminate, eventually. Stopping may mean that you get the expected output OR you get a response that no solution is possible. Algorithms must terminate after a finite number of steps.An algorithm should not be infinite and always terminate after definite number of steps. There is no point in developing an algorithm which is infinite as it will be useless for us.
🚀 Feasibility
For an algorithm to be effective, it means that all those steps that are required to get to output must be feasible with the available resources. It should not contain any unnecessary and redundant steps which could make an algorithm ineffective. For example, suppose you are cooking a recipe and you chop vegetables which are not be used in the recipe then it is a waste of time.
🚀 Independent
An algorithm should have step-by-step directions, which should be independent of any programming code.It should be such that it could be run on any of the programming languages.

Algorithms are generally created independent of underlying languages, i.e. an algorithm can be implemented in more than one programming language.
From the data structure point of view, following are some important categories of algorithms −
🚀 Search − Algorithm to search an item in a data structure.
🚀 Sort − Algorithm to sort items in a certain order.
🚀 Insert − Algorithm to update an existing item in a data structure.
🚀 Update − Algorithm to search an item in a data structure.
🚀 Delete − Algorithm to delete an existing item from a data structure.
How to Write an Effective Algorithm?
There are no well-defined standards for writing algorithms. Rather, it is problem and resource dependent. Algorithms are never written to support a particular programming code. As we know that all programming languages share basic code constructs like loops (do, for, while), flow-control (if-else), etc. These common constructs can be used to write an algorithm. We write algorithms in a step-by-step manner, but it is not always the case. Algorithm writing is a process and is executed after the problem domain is well-defined. That is, we should know the problem domain, for which we are designing a solution.
🚀 Step – 1 : Obtain detailed information on the problem.
It is a very important step in writing an algorithm. Before starting with an algorithm the programmer must obtain maximum information about the problem that needs to be solved.
🚀 Step – 2 : Analyze the problem.
Proper Analysis of the problem must be done including the data that must be gained, processed and retrieved for generating a valid output. This step helps the programmer with various processes that must be attained while generating the output along with structure and type of data.
🚀 Step – 3 : Think of a problem solving approach.
This is a very important and the most difficult step in writing an algorithm. The programmer has to come up with a problem solving approach that will help us to build the model to solve the given problem. Experience and practice is an important factor in thinking the problem solving approach. So make sure you try writing different algorithm and reading algorithms that will assist you for better understanding.
🚀 Step – 4 : Develop a basic structure of the Algorithm.
Develop a basic structure of the problem solving approach; explain the approach step-by-step with short and effective description.
🚀 Step – 5 : Optimize, Improve and refine.
After developing an Algorithm try optimizing the explanation to increase readability and accessibility of it. Also try Improving and refining the algorithm for better understanding and efficient for use.
Types of Algorithm
Brute Force Algorithm: The simplest possible algorithm that can be devised to solve a problem is called the brute force algorithm. To device an optimal solution first we need to get a solution at least and then try to optimise it. Every problem can be solved by brute force approach although generally not with appreciable space and time complexity.
Greedy Algorithm : In this algorithm, a decision is made that is good at that point without considering the future. This means that some local best is chosen and considers it as the global optimal. There are two properties in this algorithm.
1. Greedily choosing the best option
2. Optimal substructure property: If an optimal solution can be found by retrieving the optimal solution to its subproblems.
Greedy Algorithm does not always work but when it does, it works like a charm! This algorithm is easy to device and most of the time the simplest one. But making locally best decisions does not always work as it sounds. So, it is replaced by a reliable solution called Dynamic Programming approach.
Recursive Algorithm: This is one of the simplest to devise algorithms as it does not require specifically think about every subproblem. This means we just need to think about the existing cases and the solution of the simplest subproblem, all other complexity will be handled by it automatically. Recursion is a very powerful tool although we should always take care of memory management here as recursion works using recursive stack which is called every time recursion function is invoked. Recursion simply means calling itself to solve its subproblems.
Backtracking Algorithm : It is an improvement to the brute force approach. Here we start with one possible option out of many available and try to solve the problem if we are able to solve the problem with the selected move then we will print the solution else we will backtrack and select some other and try to solve it. It is a form of recursion, it’s just that when a given option cannot give a solution, we backtrack to the previous option which can give a solution, and proceed with other options.
Divide & Conquer Algorithm : This is one of the most used algorithms in programming. This algorithm divides the problems into subproblems and then solve each of them and then combine them to form the solution of the given problems.Again, it is not possible to solve all problems using it. As the name suggests it has two parts: Divide the problem into subproblems and solve them.
1. Combine the solution of each above problems.
2. This algorithm is extensively used in various problems as it is quite stable and optimal for most of the problems asked.
Dynamic Algorithm : This is the most sought out algorithm as it provides the most efficient way of solving a problem. Its simply means remembering the past and apply it to future corresponding results and hence this algorithm is quite efficient in terms of time complexity.
This is the most sought out algorithm as it provides the most efficient way of solving a problem. Its simply means remembering the past and apply it to future corresponding results and hence this algorithm is quite efficient in terms of time complexity.
1. Optimal Substructure: An optimal solution to a problem contains an optimal solution to its subproblems.
2. Overlapping subproblems: A recursive solution contains a small number of distinct subproblems.
This algorithm has two version:
Bottom-Up Approach: Starts solving from the bottom of the problems i.e. solving the last possible subproblems first and using the result of those solving the above subproblems.
Top-Down Approach: Starts solving the problems from the very beginning to arrive at the required subproblem and solve it using previously solved subproblems.

How to Get Better at Algorithms
Ah, one of the many age-old questions. How do we get better at any skill? The simple — and annoying — answer is to practice. Like OOD and programming in general, experiencing challenges and learning from them is probably the best way to get better.
But you can speed up the process by learning about existing algorithms and implementing them yourself in different languages or different ways.
🚀 Studying Existing Algorithms
It’s inarguably a good thing to understand the algorithms that form the foundation of a lot of fundamental concepts of programming. Here you want to dive into the details of an established algorithm to understand what it’s doing and why – emphasis on the ‘why’. Personally, I need to reimplement it to understand it best.
🚀 Practice Makes Better: Suggestions for Practicing
As with every skill, practicing it makes you better at it. However, the way you improve is different from physical skills, where you can perform it over and over again the same way and slowly get better. How many times can you write a heapsort in Python and still improve? I don’t actually know the answer, but I’d guess it’s not many.
Algorithm Complexity and Big O Notation
In software engineering, developers can write a program in several ways. For instance, there are many ways to search an item within a data structure. You can use linear search, binary search, jump search, interpolation search, among many other options. Our focus in this lesson is on mastering Algorithm Complexity and Big O Notation. But what we want to do with this knowledge is to improve the performance of a software application. This is why it's important to understand which algorithm to use, depending upon the problem at hand.
Algorithm complexity can be further divided into two types: time complexity and space complexity. Let's briefly touch on these two:
The time complexity, as the name suggests, refers to the time taken by the algorithm to complete its execution.
The space complexity refers to the memory occupied by the algorithm.
Big(O) Notation
Let's now talk about Big(O) Notation. Given what we've seen, you may ask-- why do we need Big O if we can just measure execution speed?
Clock time is hardware dependent. An efficient program may take more time to execute on a slower computer than an inefficient program on a fast computer. How do we compare the algorithm complexity of two programs in a standardized manner? The answer is Big(O) notation.
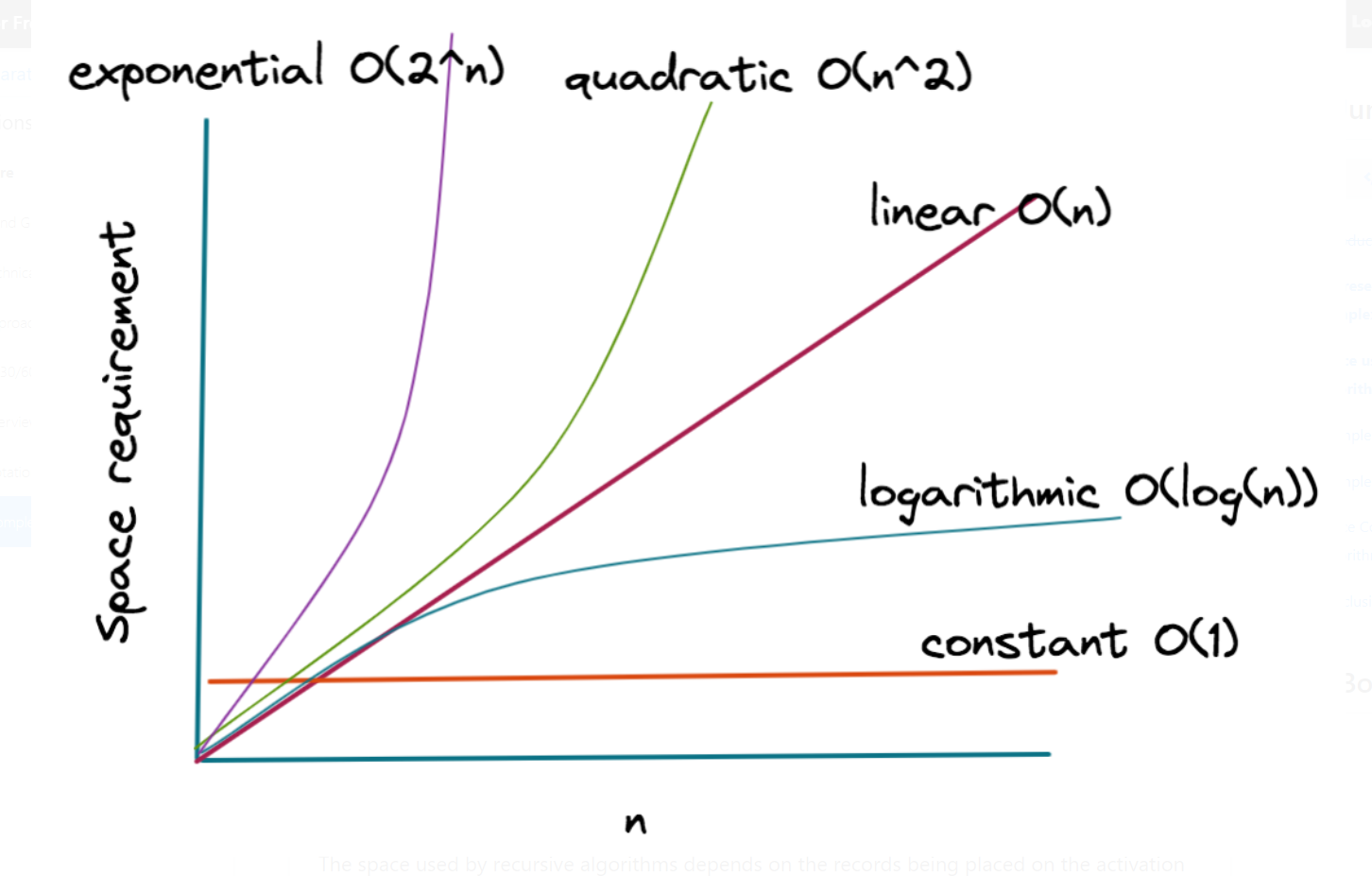
| Function with their algorithmic time complexity |
|---|
Constant - O(c) |
Logarithmic - O(log(n)) |
Linear - O(n) |
Quadratic - O(n2) |
Cubic - O(n3) |
Exponential - O(2n) |
Factorial - O(n!) |
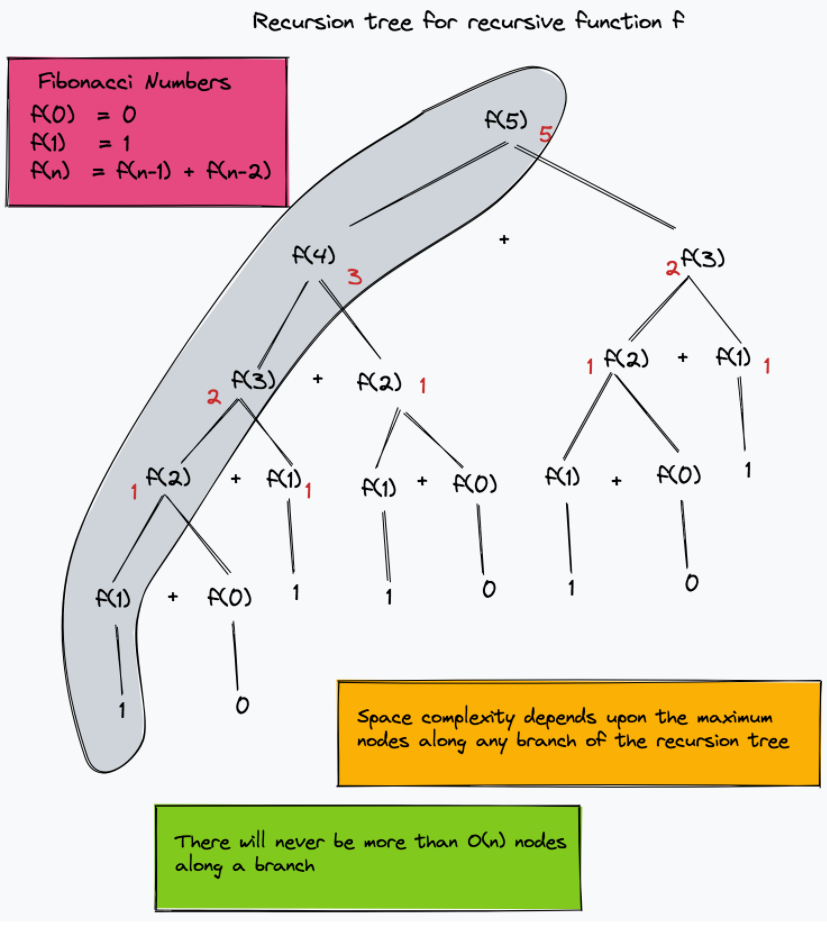
Space used by recursive algorithms
The space used by recursive algorithms depends on the records being placed on the activation stack. The general rule is to count the maximum number of activation records on the stack at any given time. If you generate a recursion tree of the program, then the space complexity would depend upon the total levels (depth) of the tree. You also carefully need to consider the variables being placed on the activation stack. An array being passed by reference to each recursive call would count as O(n). However, if the array is passed by value, then you need to take into account each copy of the array along with the maximum number of activation records in memory. In the example below, the recursion tree for the recursive computation of Fibonacci numbers is shown. The figure shows that there won't be more than O(n) instances of the function f along any branch of the recursion tree at any given time. Hence the space complexity is O(n).
Algorithms are now being used in almost every field like data science, machine learning, agriculture, science, transport, etc. Algorithms are the reason which differs every application from each other like Google Chrome from Mozilla Firefox, Uber from Ola, etc. For example, Google Chrome and Mozilla Firefox are both search engine applications and provide the same results but the order of results varies, this is because of different sorting algorithms being used. Google has its sorting algorithm which is different from that of Firefox’s.
“If every algorithm suddenly stopped working, it would be the end of the world as we know it.”
-(The Master of Algorithm by Pedro Domingos)
Happy Learning!!