Unlock the complete
Logicmojo experience for FREE

1 Million +

Strong Tech Community

500 +

Questions to Practice

100 +

Expert Interview Guides

Advanced
Data Structures Algorithms & System Design(HLD+LLD)
by Logicmojo

Cracking FAANG companies interviews with a few months of preparation

Learn Advanced Data Structures, Algorithms & System Design

Online live classes from 4 to 7 months programs

Get job assistance after course completion

Download Course Brochure

Go To Live Courses ⇲
Powered by Logicmojo

3Sum

Back to home
Logicmojo - Updated Feb 28, 2023



Problem Statement: 3Sum

Given an array of n integers, are there elements a, b, c in nums such that a + b + c = 0? Find all unique triplets in the array which gives the sum of zero.

For example:


Input: nums = [-1,0,1,2,-1,-4]


Output: [[-1,-1,2],[-1,0,1]]



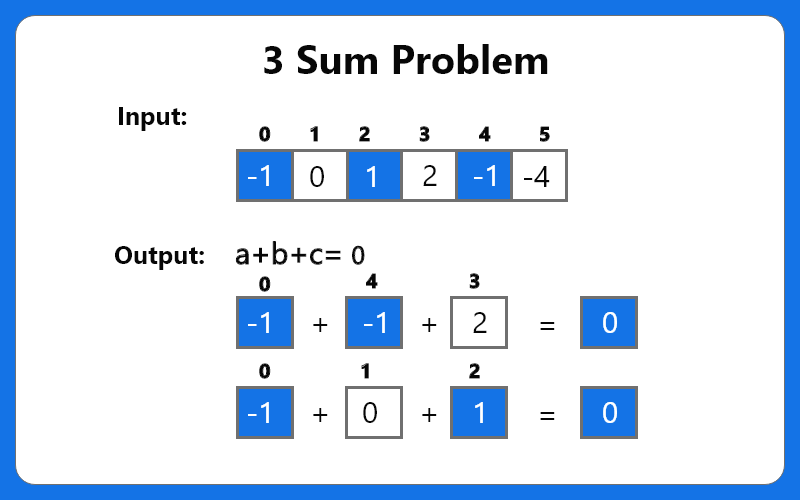
We have presented two approaches to find the two elements:

 •(Brute Force + Binary Search)
 • Two pointer solution


Approach 1: (Brute Force + Binary Search)

Let's imagine we know the values of a and b, and we want to find unique triplets with a+b+c =0. Using the equation (a+b+c =0), we can find the value of c, which is -(a+b).

We can get all pairs of a,b using two nested for loops if we take all possible (a,b) pairs. Then we may use binary search to see if c=-(a+b) is present in the given array.

Crack your next tech interview with confidence!


if it exists then the triplet (a,b,-(a+b)) will be a possible triplet. in this way, we will get all the possible triplets with a+b+c=0, but we need to find the unique triplets,for that we can insert all these possible triplets in some data structure( i.e. set) to get unique triplets.

C++ Implementation:

#include<bits/stdc++.h>
using namespace std;
vector<vector<int>> threeSum(vector<int>& nums) {
    
    set<vector<int>> s;
    
    sort(nums.begin(),nums.end());
    
    int n=nums.size();
    
    vector<int> temp;
    
    temp.resize(3);
    
    for(int i=0;i<n;i++)
        for(int j=i+1;j<n;j++)
        {
            if(binary_search(nums.begin()+j+1,nums.end(),-nums[i]-nums[j])){
                temp[0]=nums[i],temp[1]=nums[j],temp[2]=-nums[i]-nums[j];
                sort(temp.begin(),temp.end());
                s.insert(temp);
            }
        }
        
    vector<vector<int>> ans;
    
    for(auto triplet: s)
        ans.push_back(triplet);
    
    return ans;
}
void display_ans(vector<vector<int>> temp)
{
    for(auto triplet : temp) 
        cout<<triplet[0]<<" "<<triplet[1]<<" "<<triplet[2]<<"\n";
}
int main()
{
    vector<int> v{-1,0,1,2,-1,-4};
    display_ans(threeSum(v));
    return 0;
}


Java Implementation:

import java.util.*;
class Main
{
 
    static boolean binary_search (int l, int r, int[]nums, int x) 
    {
        while (l <= r)
        {
            int mid = (l + r) / 2;
            if (nums[mid] == x)
	            return true;
        	else if (nums[mid] > x)
	            r = mid - 1;
        	else
	            l = mid + 1;
        }
        return false;
    }
    public static List < List < Integer >> threeSum (int[]nums)
    {
        List < List < Integer >> ans = new ArrayList < List < Integer >> ();
        Arrays.sort (nums);
        int n = nums.length;

        for (int i = 0; i < n; i++)
        {
            for (int j = i + 1; j < n; j++)
    	    {
                if (binary_search (j + 1, n - 1, nums, -(nums[i] + nums[j])))
    	        { 
                    List < Integer > t = new ArrayList < Integer > ();
                    t.add (nums[i]);
                    t.add (nums[j]);
                    t.add (-(nums[i] + nums[j]));
                    ans.add (t);
                }
                while (j + 1 < n && nums[j + 1] == nums[j])
	            j++;
            }
            while (i + 1 < n && nums[i + 1] == nums[i])
	            i++;
        }
        return ans;
    }
 
    public static void main (String args[]) 
    {
        int[] nums = { -1, 0, 1, 2, -1, -4 };
        
        for (List < Integer > list:threeSum (nums))
        {
            for (int x:list)
                System.out.print (x + " ");
            System.out.println ();
        }
    } 
}


Time complexity:O(N*N*log(N)): we are using two nested for loops to get all the possible (a,b) pair and a Binary search to know if -(a+b) exists in the array or not.

Space complexityO(N): we are using a set to get unique triplets.



Approach 2: Two pointer solution

We are looking for triplets such that a + b + c = 0.

Let's fix single number x as a and rearrange the equation:
x + b + c = 0
b + c = -x

We reduced the original problem to finding such b and c that add up to -x in O(n).

To solve this problem effectively we will use a two pointer technique.

For this solution to work we need to sort the array at first.

After this we create 2 pointers, left and right, to the first and last element of the array respectively.

While the left pointer is less then right we compute the sum of values kept at pointers.

There are three possibilities how sum compares to -x:

  1. sum < -x, we shift the left pointer to the right, because we want to increase the sum

  2. sum > -x, we shift the right pointer to the left, because we want to decrease the sum

  3. sum = -x, we found one of the solutions! We store triplet a, b, c it in the result variable, and shift the left pointer to the right



C++ Implementation:

#include<bits/stdc++.h>
using namespace std;
vector<vector<int>> threeSum(vector<int>& nums) {
       vector<vector<int>> ans;
        sort(nums.begin(),nums.end());
        int n=nums.size();
        for(int i=0;i<n; i++)
        {
            int j=i+1,k=n-1;
            while(j<n && j<k)
            {
                if(nums[j]+nums[k] == -nums[i])
                {
                    ans.push_back({nums[i],nums[j],nums[k]});
                    while(k!=0 && nums[k]==nums[k-1]) k--; 
                    while(j!=n-1 && nums[j]==nums[j+1]) j++;
                    j++,k--;
                }
                else if(nums[j]+nums[k] > -nums[i]) 
                {
                    while(k!=0 && nums[k]==nums[k-1]) k--;
                    k--;
                }
                else
                {
                    while(j!=n-1 && nums[j]==nums[j+1]) j++;
                    j++;
                }
            }
            while(i!=n-1 && nums[i]==nums[i+1]) i++;
        }
        for(auto triplet : ans)
            sort(triplet.begin(),triplet.end());
        return ans;
}
void display_ans(vector<vector<int>> temp)
{
    for(auto triplet : temp) 
        cout<<triplet[0]<<" "<<triplet[1]<<" "<<triplet[2]<<"\n";
}
int main()
{
    vector<int> v{-1,0,1,2,-1,-4};
    display_ans(threeSum(v));
    return 0;
}


Java Implementation:

import java.util.*;
class Main{
    
  public static List<List<Integer>> threeSum(int[] nums) {
       
        List<List<Integer>> ans=new ArrayList<List<Integer>>();
        Arrays.sort(nums);
        int n=nums.length;
        
        for(int i=0;i<n;i++)
        {
            int p=i+1,q=n-1;
            while(p<q)
            {
                if(nums[p]+nums[q]==-nums[i])
                { );
                    List<Integer> t=new ArrayList<Integer>();
                    t.add(nums[i]);
                    t.add(nums[p]);
                    t.add(nums[q]);
                 
                 ans.add(t);
                    
                    while(p+1<q &&  nums[p+1]==nums[p]) p++;
                    while(q-1>p &&  nums[q-1]==nums[q]) q--;
                    
                    p++; q--;
                }
                else if(nums[p]+nums[q] < -nums[i]) p++;
                else q--;
            }
            
            while(i+1<n && nums[i+1]==nums[i]) i++;
        }
        return ans;
    }
    
  public static void main(String args[])
    {
         int[] nums={-1,0,1,2,-1,-4};
        for(List<Integer> list:  threeSum(nums))
        {
            for(int x: list)
            System.out.print(x+ " ");
            System.out.println();
        }
    }
}


Python Implementation:

def threeSum(self, nums):
    """
    :type nums: List[int]
    :rtype: List[List[int]]
    """
    result = []
 
    nums.sort()
 
    for first_idx in range(len(nums)):
        if first_idx > 0 and nums[first_idx] == nums[first_idx - 1]:
            continue
 
        second_idx = first_idx + 1
        third_idx = len(nums) - 1
 
        required_sum  = 0 - nums[first_idx];
 
        while second_idx < third_idx:
            current_sum = nums[second_idx] + nums[third_idx]
 
            if current_sum < required_sum:
                second_idx += 1
            elif current_sum > required_sum:
                third_idx -= 1
            else:
                result.append([nums[first_idx], nums[second_idx], nums[third_idx]])
                second_idx += 1
                while second_idx < third_idx and nums[second_idx] == nums[second_idx - 1]:
                    second_idx += 1
 
    return result


Time Complexity: O(N^2): we are using one for loops to get values of a, and for every value of a, we find the pair b,c (such that a+b+c=0) using two pointer approach that takes O(N) time. so total time complexity is of the order of O(N^2).

Space Complexity: O(N): we are using a vector to store the answer.


With this article at Logicmojo, you must have the complete idea of solving 3Sum problem.
© 2023 Logicmojo. ALL RIGHTS RESERVED