Longest Palindromic Substring

Name: kadane's algorithm
Brand: LogicMojo
SKU: .
Availability: InStock
Rating: 4.8 (230 reviews)

Back to home

Logicmojo - Updated Dec 12, 2023

𝑻𝒂𝒃𝒍𝒆 𝒐𝒇 𝑪𝒐𝒏𝒕𝒆𝒏𝒕

Problem Statement: Longest Palindromic Substring
Brute Force Approach
Expand Around Center Approach

Problem Statement: Longest Palindromic Substring

Find and return the longest palindromic substring in a string str of length N. Substring of string str is str[i...j] where 0 <= i <= j < len(str)

Palindrome string:
A string which reads the same backwards that is if reverse(str) = str, then str is a palindrome. If there are more than one substring then return the substring that appears first.

Input Format : The string str is the first and only parameter.
Output Format : Return the longest palindromic substring of string str as a string.

Learn More️

For Example,
Input : mojologiccigolmojo
Output : logiccigol
Explanation : The longest palindromic substring is 10 characters long, and the string is logiccigol.

Input : abcdcbe
Outupt : bcdcb
Explanation : The longest palindromic substring is 5 characters long, and the string is bcdcb.

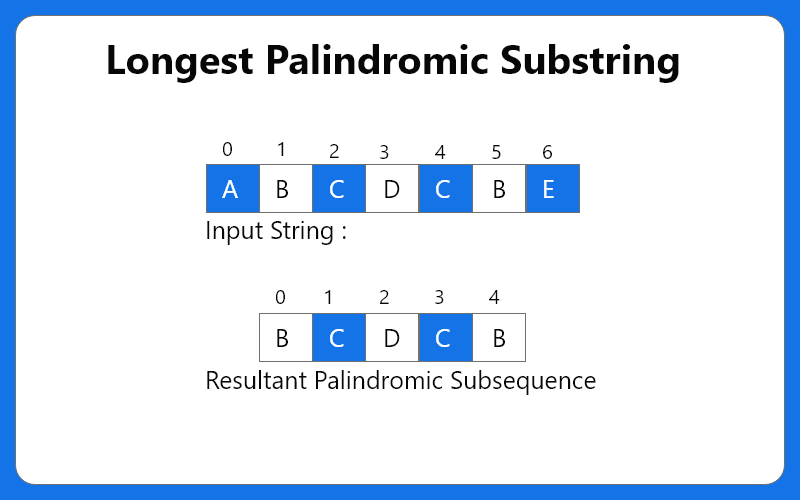
We have presented two approaches to find the longest palindromic substring :

• Brute Force Approach
• Dynamic Programming Approach
• Expand Around Center Approach

Brute Force Approach

The most straightforward method is to check whether each substring is a palindrome or not. To begin, run three nested loops: the outer two loops pick all substrings one by one by fixing the corner characters, and the inner loop tests if the substring picked is palindrome or not.

It is important to note that every substring of length "1" is a palindrome in this context.

We'll therefore initially keep a variable that simply stores the length of our input string and another variable that simply stores the maximum length of the palindrome we have encountered so far. Reversing a string and comparing it to the original string, or substring in this case, is a useful approach to determine whether a string is a palindrome.

Time complexity : O(n^3).
Three nested loops are needed to find the longest palindromic substring in this approach, so the time complexity is O(n^3).
Space complexity : O(1).
As no extra space is needed.

C++ Implementation:

#include <bits/stdc++.h>
using namespace std;

void longestPalindrome(string str)
{
	int n = str.size();
	int max = 1, start = 0;

	for (int i = 0; i < str.length(); i++) {
		for (int j = i; j < str.length(); j++) {
			int flag = 1;

			for (int k = 0; k < (j - i + 1) / 2; k++)
				if (str[i + k] != str[j - k])
					flag = 0;

			if (flag && (j - i + 1) > max) {
				start = i;
				max = j - i + 1;
			}
		}
	}

	for (int i = start; i <= start+max-1; ++i)
		cout << str[i];
}

int main()
{
	string str = "mojologiccigolmojo";
	longestPalindrome(str);
	return 0;
}

        Try it Yourself

Java Implementation:

class Main{

    public static void longestPalindrome(String str)
    {
	    int n = str.length();
	    int max = 1, start = 0;

    	    for (int i = 0; i < str.length(); i++) {
	    	for (int j = i; j < str.length(); j++) {
		    	boolean flag = true;

    			    for (int k = 0; k < (j - i + 1) / 2; k++)
	        			if (str.charAt(i + k) != str.charAt(j - k))
			        		flag = false;
    			    if (flag && (j - i + 1) > max) {
				        start = i;
				        max = j - i + 1;
			        }
		    }
	    }

        System.out.println(str.substring(start,start+max));

    }

    public static void main(String[] args)
    {
	    String str = "mojologiccigolmojo";
	    longestPalindrome(str);
	
    }
}

        Try it Yourself

Python Implementation:

def printSubStr(str, low, high):
	
	for i in range(low, high + 1):
		print(str[i], end = "")

def longestPalindrome(str):
	
	n = len(str)
	
	maxLength = 1
	start = 0
	
	for i in range(n):
		for j in range(i, n):
			flag = 1
			
			for k in range(0, ((j - i) // 2) + 1):
				if (str[i + k] != str[j - k]):
					flag = 0

			if (flag != 0 and (j - i + 1) > maxLength):
				start = i
				maxLength = j - i + 1
				
	printSubStr(str, start, start + maxLength - 1)

if __name__ == '__main__':

	str = "mojologiccigolmojo"
	
	longestPalindrome(str)

        Try it Yourself

Dynamic Programming Approach

This problem can be resolved using dynamic programming, a more efficient variation of the prior method. To reiterate, dynamic programming works by splitting up larger problems into smaller ones and applying the output of computations on the smaller problems. The outcomes of the more manageable subproblems are retained and used.

Steps to solve the problem :

Keep a boolean table[n][n] that is filled from the bottom up.
If the substring is a palindrome, the value of table[i][j] is true; otherwise, it is false.
Check the value of table[i+1][j-1] before calculating table[i][j]. If the value is true and str[i] and str[j] are identical, then table[i][j] is true.
Otherwise, table[i][j] values is set to false.
We must fill out a table in advance for substrings of lengths=1 and lengths=2 since we are determining whether table[i+1][j-1] is true or false, therefore in the event of
If length == 1, let i=2, j=2 and (i+1,j-1) not lie between [i,j].
or, length == 2, let's say that i=2 and j=3, and that once more i+1 and j-1 do not lie between [i,j].

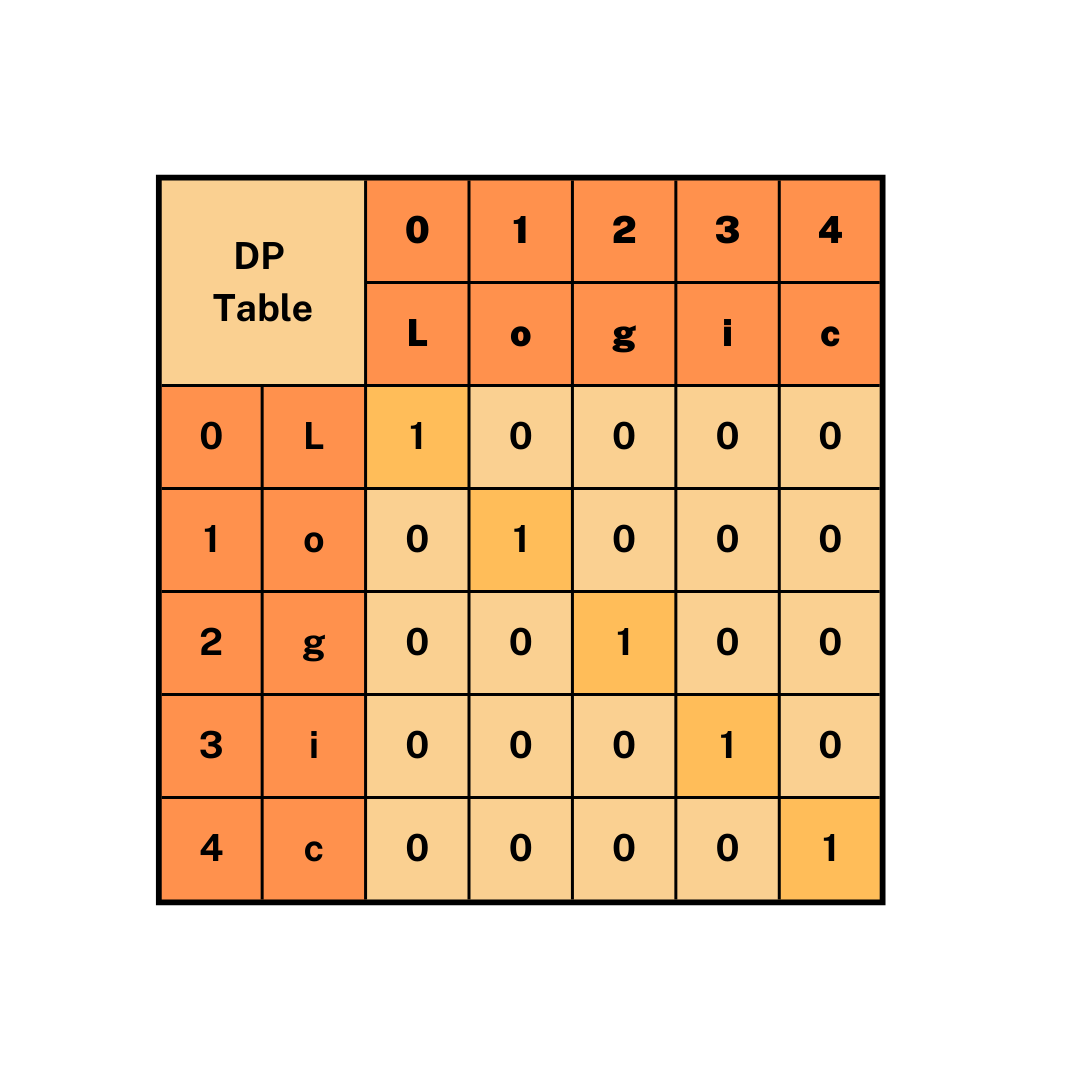
Time complexity : O(n^2).
Given that we need two nested traversals of the string, this strategy has a lower temporal complexity than the naïve or brute force solution, but it is still not the best option, so, the overall complexity is O(n^2).
Space complexity : O(n^2).
The dynamic programming approach's space complexity is O because we store the results of the subproblems in a table of size n * n. (n2).

C++ Implementation:

#include <bits/stdc++.h>
using namespace std;
 
// Function to print a substring
void printSubs(
    string s, int low, int high)
{
    for (int i = low; i <= high; ++i)
        cout << str[i];
}
 
// longest palindrome substring
    int longestPalSubs(string s)
{
    int n = s.size();

    bool table[n][n];
 
    memset(table, 0, sizeof(table));
    int maxlen = 1;
 
    for (int i = 0; i < n; ++i)
        table[i][i] = true;
 
    // check for sub-string of length 2.
    int start = 0;
    for (int i = 0; i < n - 1; ++i) {
        if (s[i] == s[i + 1]) {
            table[i][i + 1] = true;
            start = i;
            maxlen = 2;
        }
    }
 
    // k is length of substring
    for (int k = 3; k <= n; ++k) {
        for (int i = 0; i < n - k + 1; ++i) {

            // starting index i and length k
            int j = i + k - 1;
 
            if (table[i + 1][j - 1] && s[i] == s[j]) {
                table[i][j] =  true;
 
                if (k > maxlen) {
                    start = i;
                    maxlen = k;
                }
            }
        }
    }
 
    cout << "Longest Palindrome Substring is: ";
    printSubStr(s, start, start + maxLength - 1);
 
    // return length of LongestPalindromeSubstring
    return maxlen;
}
 
int main()
{
    string s = "mojologiccigolmojo";
    cout << "\nlen is: "
         << longestPalSubs(s);
    return 0;
}
          
                        
        Try it Yourself

Java Implementation:

public class longestPalSubstring {
    
    // a substring s[low..high]
    static void printSubs(
        String s, int low, int high)
    {
        System.out.println(
            s.subs(
                low, high + 1));
    }
 
    // This function prints the longest
    static int longestPalSubstr(String s)
    {
        // get length of input string
        int n = s.len();

        boolean table[][] = new boolean[n][n];
 
        // All substrings of length 1 are palindromes
        int maxlen = 1;
        for (int i = 0; i < n; ++i)
            table[i][i] = true;
 
        // check for sub-string of length 2.
        int start = 0;
        for (int i = 0; i < n - 1; ++i) {
            if (s.charAt(i) == s.charAt(i + 1)) {
                table[i][i + 1] = true;
                start = i;
                maxlen = 2;
            }
        }
 
        // k is length of substring
        for (int k = 3; k <= n; ++k) {
 
            for (int i = 0; i < n - k + 1; ++i) {
        
                // starting index i and length k
                int j = i + k - 1;
 
                if (table[i + 1][j - 1]
                    && s.charAt(i) == s.charAt(j)) {
                    table[i][j] = true;
 
                    if (k > maxlen) {
                        start = i;
                        maxlen = k;
                    }
                }
            }
        }
        System.out.print("Longest palindrome substring is; ");
        printSubS(s, start,
                    start + maxlen - 1);
 
        // return length of LongestPalindromeSubstring
        return maxLength;
    }
    public static void main(String[] args)
    {
 
        String str = "mojologiccigolmojo";
        System.out.println("len is: " + longestPalSubs(s));
    }
}
          
                        
        Try it Yourself

Python Implementation:

import sys

def printSubS(s, low, high) :
    sys.stdout.write(st[low : high + 1])
    sys.stdout.flush()
    return ''
 
# This function prints the longest palindrome
def longestPalSubs(s) :
    n = len(s) 
    table = [[0 for x in range(n)] for y
                          in range(n)]
    maxlen = 1
    i = 0
    while (i < n) :
        table[i][i] = True
        i = i + 1
     
    start = 0
    i = 0
    while i < n - 1 :
        if (s[i] == s[i + 1]) :
            table[i][i + 1] = True
            start = i
            maxlen = 2
        i = i + 1
   
    k = 3
    while k <= n :
        i = 0
        while i < (n - k + 1) :
         
            # index i and length k
            j = i + k - 1
     
            if (table[i + 1][j - 1] and
                      s[i] == s[j]) :
                table[i][j] = True
     
                if (k > maxlen) :
                    start = i
                    maxlen = k
            i = i + 1
        k = k + 1
    print "Longest palindrome substring is: ", printSubS(s, start,
                                               start + maxlen - 1)
    # return length of LongestPalindromeSequence
    return maxLength 
 
s = "mojologiccigolmojo"
l = longestPalSubs(s)
print "Length is:", l
          
                        
        Try it Yourself

Optimal Solution: Expand Around center

The concept is straightforward: take each character in the given string to be the midpoint of a palindrome and extend in both directions to discover the longest palindrome possible. For an even length palindrome, consider every adjacent pair of characters as the midpoint.

Let's take a example, for that palindrome is - "wowwow"

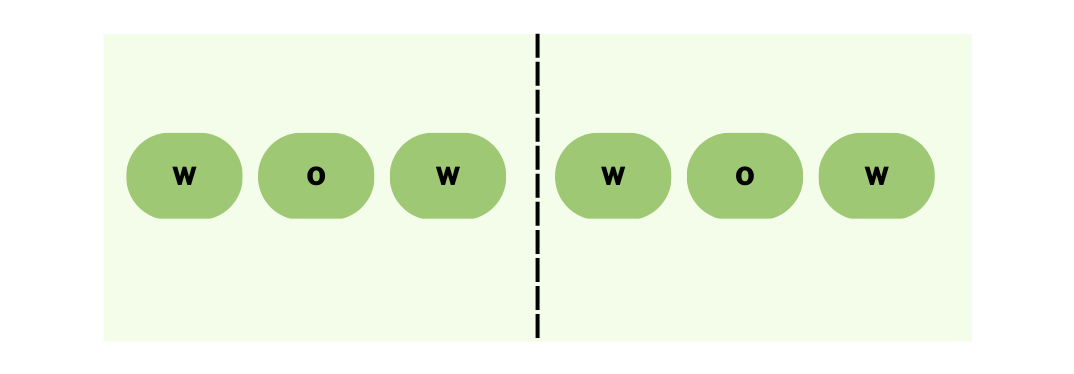
Time complexity : O(n^2).
Since expanding a palindrome around its center could take O(n) time, the overall complexity is O(n^2).
Space complexity : O(1).

C++ Implementation:

#include <iostream>
#include <string>
using namespace std;
 

string expand(string str, int low, int high)
{
    while (low >= 0 && high < str.length() && (str[low] == str[high])) {
        low--, high++;       
    }
    return str.substr(low + 1, high - low - 1);
}
 
string longestPalindromicSubstring(string str)
{
    if (str.length() == 0) {
        return str;
    }
    
    string max_str = "", curr_str;
 
    int max_length = 0, curr_length;
 
    for (int i = 0; i < str.length(); i++)
    {
    
        curr_str = expand(str, i, i);
        curr_length = curr_str.length();
 
        if (curr_length > max_length)
        {
            max_length = curr_length;
            max_str = curr_str;
        }
 
        curr_str = expand(str, i, i + 1);
        curr_length = curr_str.length();
 
        if (curr_length > max_length)
        {
            max_length = curr_length;
            max_str = curr_str;
        }
    }
 
    return max_str;
}
 
int main()
{
    string str = "mojologiccigolmojo";
 
    cout <<longestPalindromicSubstring(str);
 
    return 0;
}

        Try it Yourself

Java Implementation:

#include <iostream>
#include <string>
using namespace std;
 

string expand(string str, int low, int high)
{
    while (low >= 0 && high < str.length() && (str[low] == str[high])) {
        low--, high++;       
    }
    return str.substr(low + 1, high - low - 1);
}
 
string longestPalindromicSubstring(string str)
{
    if (str.length() == 0) {
        return str;
    }
    
    string max_str = "", curr_str;
 
    int max_length = 0, curr_length;
 
    for (int i = 0; i < str.length(); i++)
    {
    
        curr_str = expand(str, i, i);
        curr_length = curr_str.length();
 
        if (curr_length > max_length)
        {
            max_length = curr_length;
            max_str = curr_str;
        }
 
        curr_str = expand(str, i, i + 1);
        curr_length = curr_str.length();
 
        if (curr_length > max_length)
        {
            max_length = curr_length;
            max_str = curr_str;
        }
    }
 
    return max_str;
}
 
int main()
{
    string str = "mojologiccigolmojo";
 
    cout <<longestPalindromicSubstring(str);
 
    return 0;
}

        Try it Yourself

Python Implementation:

def expand(s, low, high):
    length = len(s)
 
    while low >= 0 and high < length and s[low] == s[high]:
        low = low - 1
        high = high + 1
 
    return s[low + 1:high]
 
 
def findLongestPalindromicSubstring(s):
 
    if not s or not len(s):
        return ''
 
    max_str = ''
 
    max_length = 0
 
    for i in range(len(s)):
        curr_str = expand(s, i, i)
        curr_length = len(curr_str)
 
        if curr_length > max_length:
            max_length = curr_length
            max_str = curr_str
 
        curr_str = expand(s, i, i + 1)
        curr_length = len(curr_str)
 
        if curr_length > max_length:
            max_length = curr_length
            max_str = curr_str
 
    return max_str
 
if __name__ == '__main__':
 
    s = 'mojologiccigolmojo'
 
    print(findLongestPalindromicSubstring(s))

        Try it Yourself

With this article at Logicmojo, you must have the complete idea of solving Longes Palindromic Substring.

Unlock the complete
Logicmojo experience for FREE

1 Million +

500 +

50 +

Longest Palindromic Substring

𝑻𝒂𝒃𝒍𝒆 𝒐𝒇 𝑪𝒐𝒏𝒕𝒆𝒏𝒕

Problem Statement: Longest Palindromic Substring

Brute Force Approach

Dynamic Programming Approach

Optimal Solution: Expand Around center

Unlock the complete Logicmojo experience for FREE

1 Million +

500 +

50 +

Advanced Data Structures Algorithms & System Design(HLD+LLD) by Logicmojo

Longest Palindromic Substring

𝑻𝒂𝒃𝒍𝒆 𝒐𝒇 𝑪𝒐𝒏𝒕𝒆𝒏𝒕

Problem Statement: Longest Palindromic Substring

Brute Force Approach

Dynamic Programming Approach

Optimal Solution: Expand Around center

Unlock the complete
Logicmojo experience for FREE

Advanced
Data Structures Algorithms & System Design(HLD+LLD)
by Logicmojo