Let’s say we have 8 houses. We want to setup telephone lines between these houses. The edge between the houses represent the cost of setting line between two houses.

Our task is to set up lines in such a way that all the houses are connected and the cost of setting up the whole connection is minimum. Now how do we find that out? We can use Prim’s Algorithm.

Prim’s Algorithm is a greedy algorithm that finds a minimum spanning tree for a weighted undirected graph. This means it finds a subset of the edges that forms a tree that includes every node, where the total weight of all the edges in the tree are minimized.

What is Spanning Tree?

A spanning tree of a connected graph G can be defined as a maximal set of edges of G that contains no cycle, or as a minimal set of edges that connect all vertices.

What is Minimum Spanning Tree?

• It is a tree (i.e., it is acyclic).
• It covers all the vertices V – contains |V| — 1 edges.
• The total cost associated with tree edges is the minimum among all possible spanning trees.
• not necessarily unique.

Implementation of Prim’s Algorithm

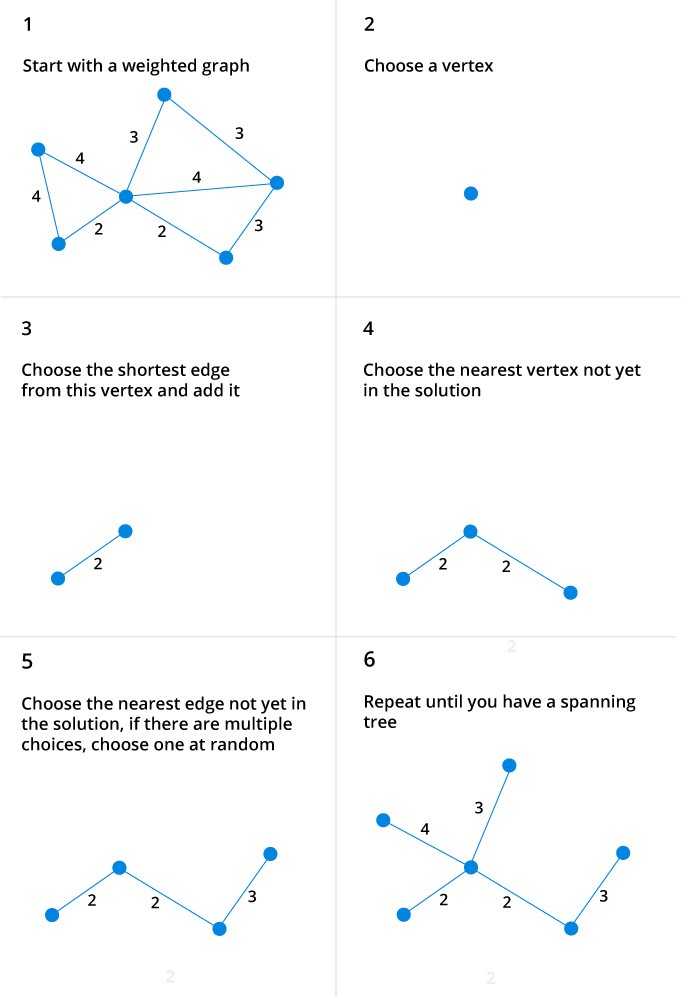
We start from one vertex and keep adding edges with the lowest weight until we we reach our goal.

The steps for implementing Prim’s algorithm are as follows:

1. Initialize the minimum spanning tree with a vertex chosen at random.
2. Find all the edges that connect the tree to new vertices, find the minimum and add it to the tree
3. Keep repeating step 2 until we get a minimum spanning tree

Prim’s Algorithm Applications:

General Applications:
1. Distances between the cities for the minimum route calculation for transportation.
2.For Establishing the network cables these play important role in finding the minimum cables required to cover the whole region
3. Applications in CS Domains:
 1.All this path finding algorithms are used in AI (Artificial Intelligence)
 2.Game Development

Implementation in Python

# Prim's Algorithm in Python

INF = 9999999
# number of vertices in graph
N = 5
#creating graph by adjacency matrix method
G = [[0, 19, 5, 0, 0],
     [19, 0, 5, 9, 2],
     [5, 5, 0, 1, 6],
     [0, 9, 1, 0, 1],
     [0, 2, 6, 1, 0]]

selected_node = [0, 0, 0, 0, 0]

no_edge = 0

selected_node[0] = True

# printing for edge and weight
print("Edge : Weight\n")
while (no_edge < N - 1):
    
    minimum = INF
    a = 0
    b = 0
    for m in range(N):
        if selected_node[m]:
            for n in range(N):
                if ((not selected_node[n]) and G[m][n]):  
                    # not in selected and there is an edge
                    if minimum > G[m][n]:
                        minimum = G[m][n]
                        a = m
                        b = n
    print(str(a) + "-" + str(b) + ":" + str(G[a][b]))
    selected_node[b] = True
    no_edge += 1

        Try it Yourself 

Implementation in C++

// Prim's Algorithm in C++

#include <cstring>
#include <iostream>
using namespace std;

#define INF 9999999

// number of vertices in grapj
#define V 5

// create a 2d array of size 5x5
//for adjacency matrix to represent graph

int G[V][V] = {
  {0, 9, 75, 0, 0},
  {9, 0, 95, 19, 42},
  {75, 95, 0, 51, 66},
  {0, 19, 51, 0, 31},
  {0, 42, 66, 31, 0}};

int main() {
  int no_edge;  // number of edge

  // create a array to track selected vertex
  // selected will become true otherwise false
  int selected[V];

  // set selected false initially
  memset(selected, false, sizeof(selected));

  // set number of edge to 0
  no_edge = 0;

  // the number of egde in minimum spanning tree will be
  // always less than (V -1), where V is number of vertices in
  //graph

  // choose 0th vertex and make it true
  selected[0] = true;

  int x;  //  row number
  int y;  //  col number

  // print for edge and weight
  cout << "Edge"
     << " : "
     << "Weight";
  cout << endl;
  while (no_edge < V - 1) {
    //For every vertex in the set S, find the all adjacent vertices
    // , calculate the distance from the vertex selected at step 1.
    // if the vertex is already in the set S, discard it otherwise
    //choose another vertex nearest to selected vertex  at step 1.

    int min = INF;
    x = 0;
    y = 0;

    for (int i = 0; i < V; i++) {
      if (selected[i]) {
        for (int j = 0; j < V; j++) {
          if (!selected[j] && G[i][j]) {  // not in selected and there is an edge
            if (min > G[i][j]) {
              min = G[i][j];
              x = i;
              y = j;
            }
          }
        }
      }
    }
    cout << x << " - " << y << " :  " << G[x][y];
    cout << endl;
    selected[y] = true;
    no_edge++;
  }

  return 0;
}

        Try it Yourself 

Time & Space Complexity Analysis

The running time for prim’s algorithm is O(VlogV + ElogV) which is equal to O(ElogV) because every insertion of a node in the solution takes logarithmic time. Here, E is the number of edges and V is the number of vertices/nodes. However, we can improve the running time complexity to O(E + logV) of prim’s algorithm using Fibonacci Heaps.

With this article at Logicmojo, you must have the complete idea of analyzing Prim's Algorithm.

Good Luck & Happy Learning!!