 Logicmojo - Updated Jan 8, 2025
Logicmojo - Updated Jan 8, 2025
Introduction
Quick sort is an efficient sorting algorithm that uses a divide and conquer strategy to sort a list of items, quicksort divides a huge array of data into smaller sub-arrays. By dividing the input into two parts, sorting them, and then recombining them, it is implied that each iteration operates in this method. It works by first selecting a pivot element from the list and then dividing the list into two sub-lists based on the pivot. Items in the sub-lists are then recursively sorted until the list is completely sorted. Quick sort is generally considered to be one of the most efficient sorting algorithms, with an average time complexity of O(n log n).
Tony Hoare developed it in 1961, and it is still among the best all-purpose sorting algorithms on the field.How Quick-Sort Works
You should perform the actions listed below to sort an array using Quick-sort:
- Any index value in the array will work as the pivot.
- The array will then be separated based on the pivot.
- Next, quicksort the left partition recursively.
- You will then recursively quicksort the proper partition after that.
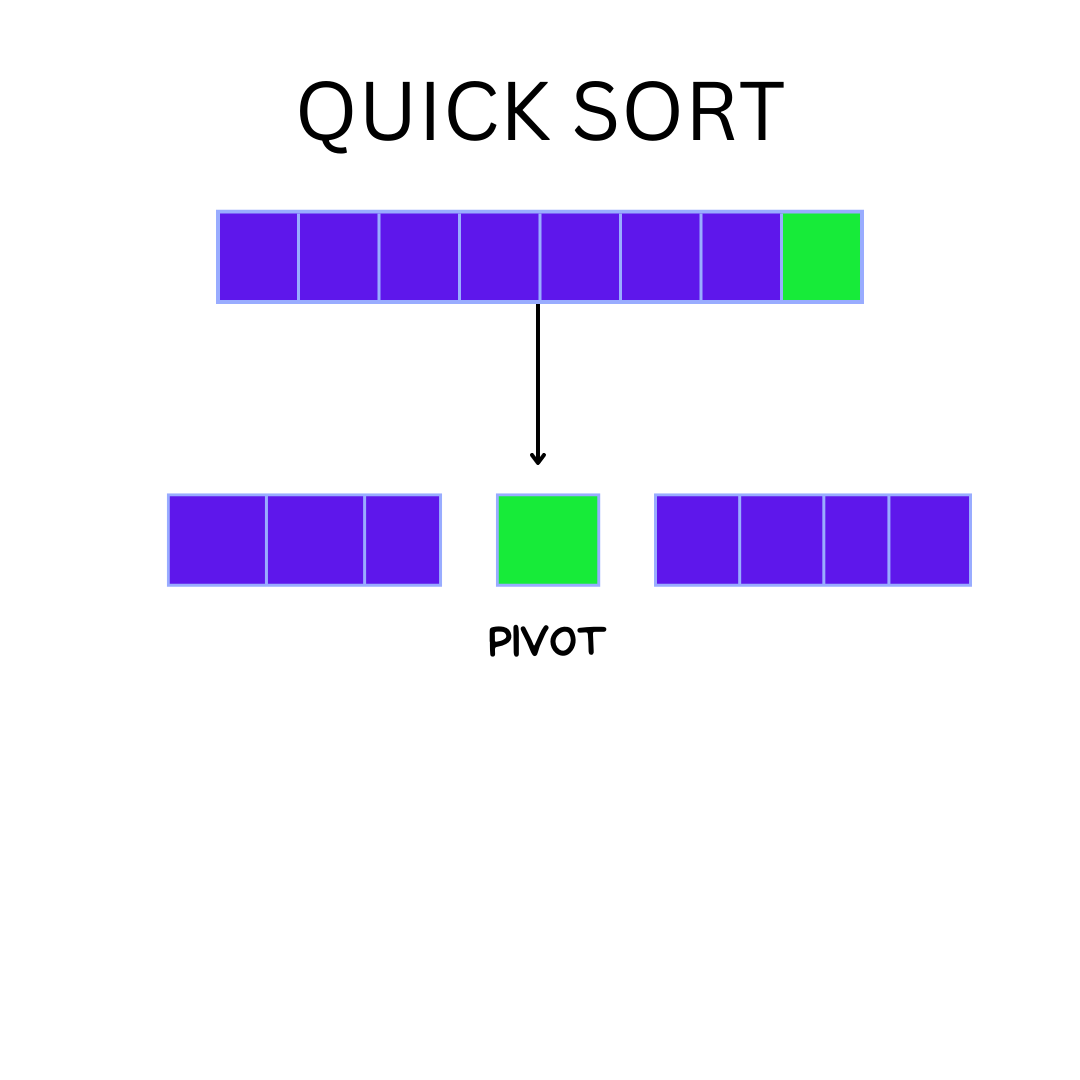
DIVIDE: Choose a pivot point, first. The array should then be divided or rearranged into two sub-arrays with each element in the left sub-array being smaller than or equal to the pivot element and each element in the right sub-array being greater than the pivot element.
Conquer: Recursively, sort two subarrays with Quicksort.
Combine: Combine the array once it has been sorted.
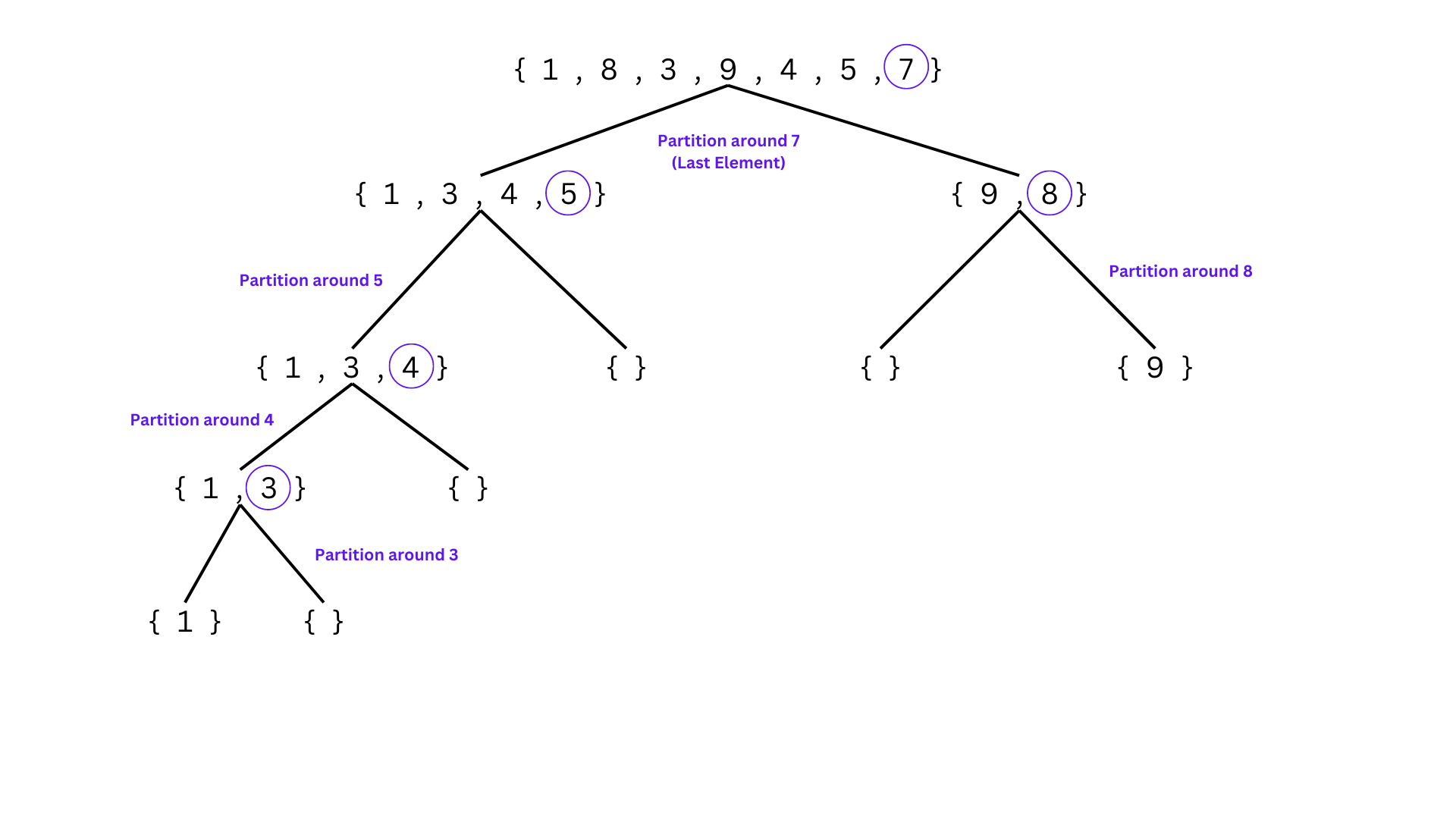
Selection of Pivot
Selection of pivot For quicksort to be implemented, a good pivot must be chosen. It is common practise to choose a decent pivot, nevertheless. Some methods for selecting a pivot include the following:
- ->The pivot can be chosen at random, i.e., from the available array.
- ->The leftmost or rightmost element of the specified array can serve as the pivot.
- ->Decide on median as the pivotal value.
Algorithm
Quick-sort Algorithm
quicksort (arr A, start, end)
{
if (start < end)
{
p = part(A, start, end)
quicksort (A, start, p - 1)
quicksort (A, p + 1, end)
}
}
Partition Algorithm
partition (array, start, end)
{
// Setting rightmost Index as pivot
pivot = arr[end];
i = (start - 1) // Index of smaller element and indicates the
// right position of pivot found so far
for (j = start; j <= end- 1; j++)
{
// If current element is smaller than the pivot
if (arr[j] < pivot)
{
i++; // increment index of smaller element
swap arr[i] and arr[j]
}
}
swap arr[i + 1] and arr[end])
return (i + 1)
}
Example of Quick-sort
Let us take a simple example to understand Quick-sort better, after going through with this example you will understand how quick-sort works:-
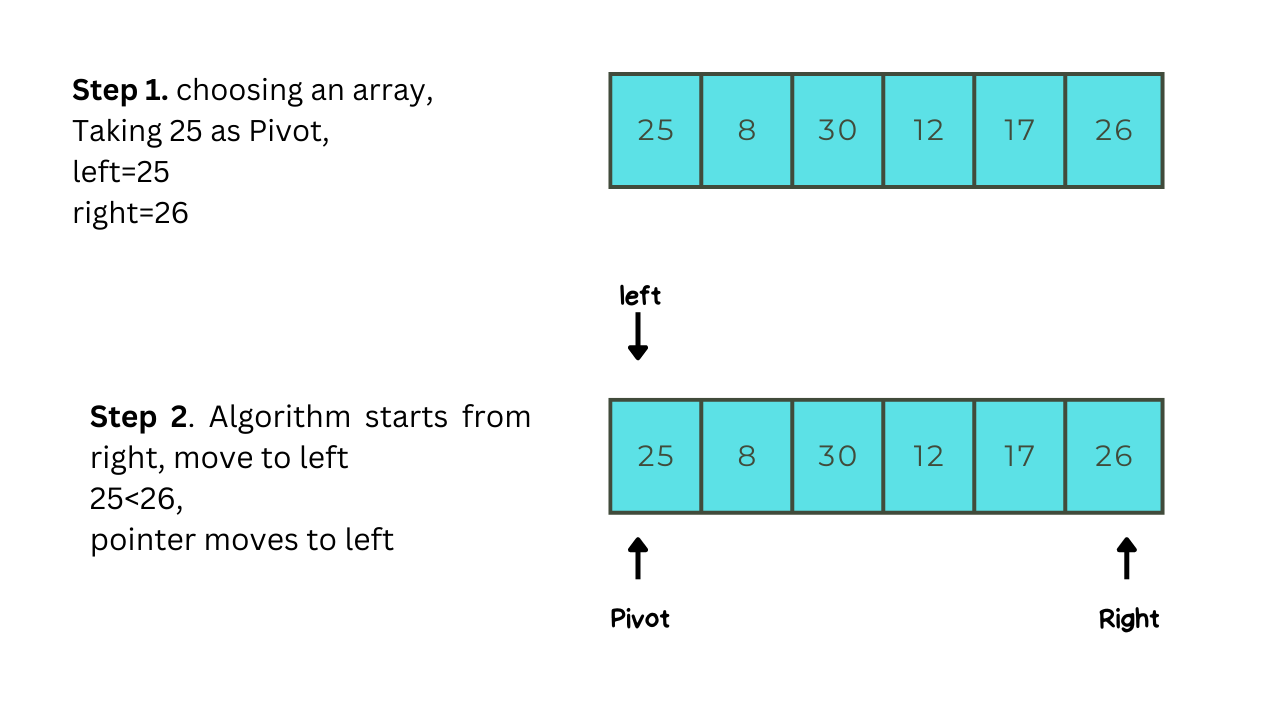
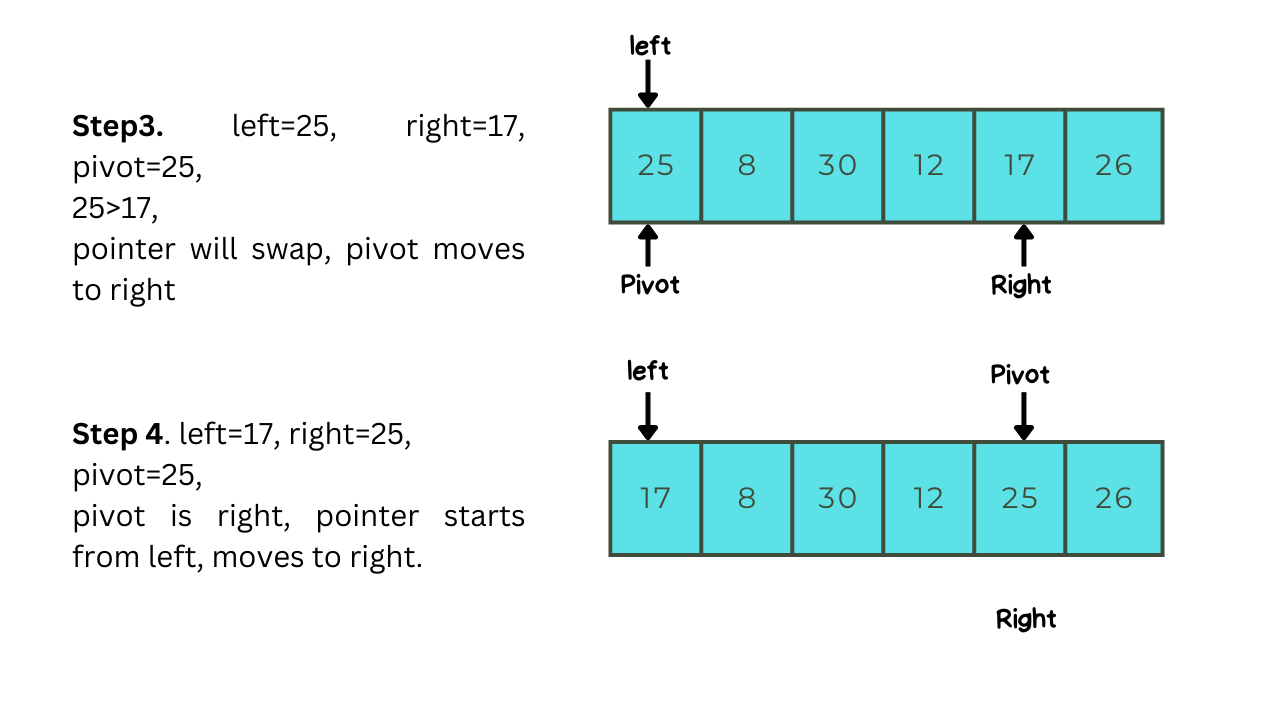
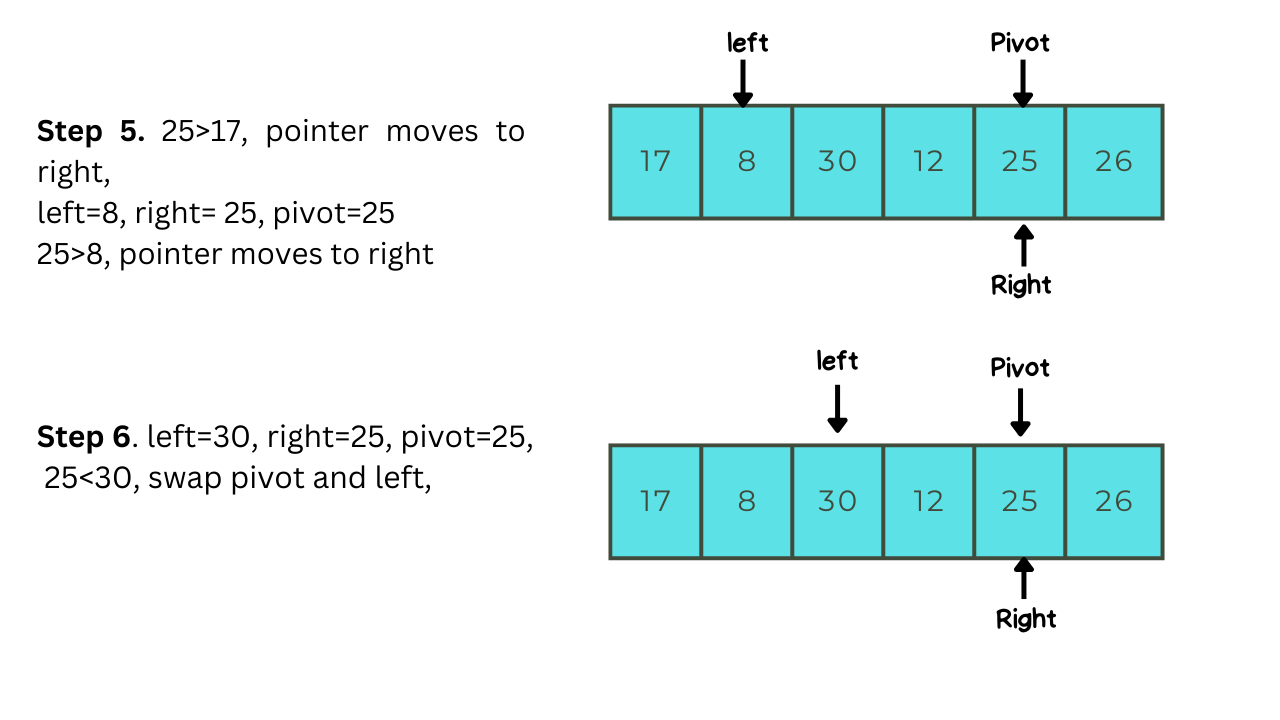
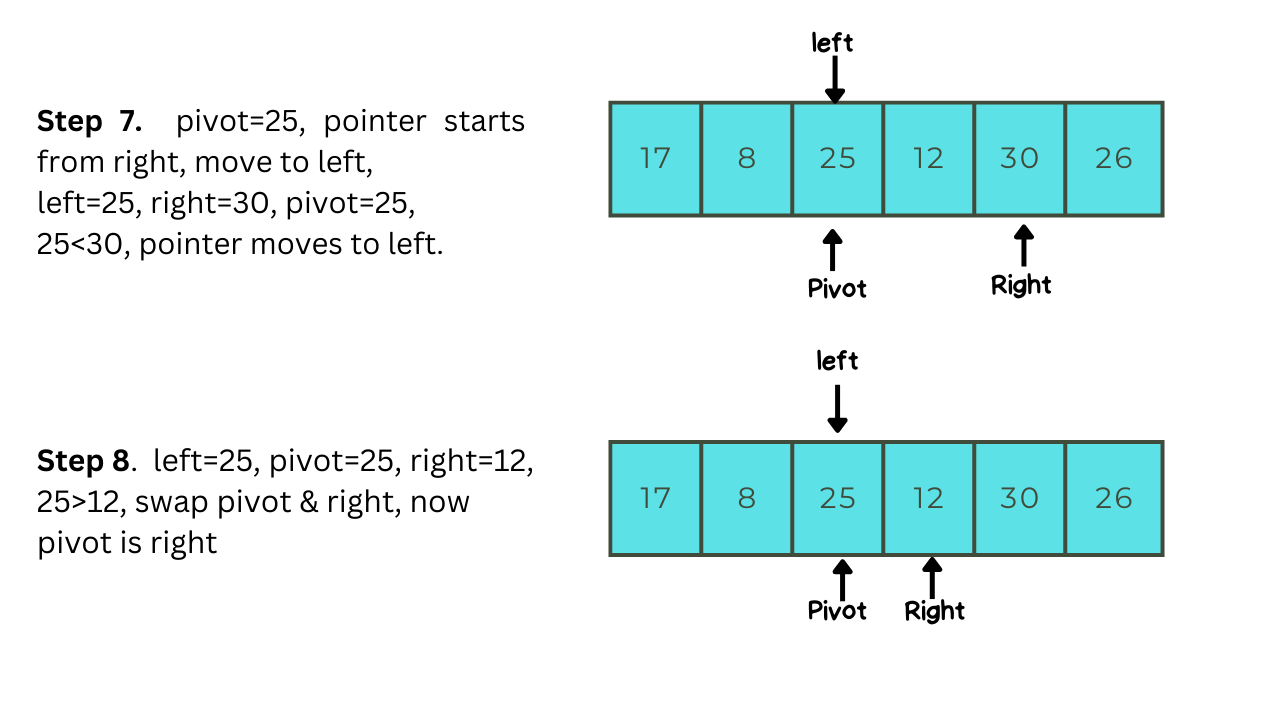
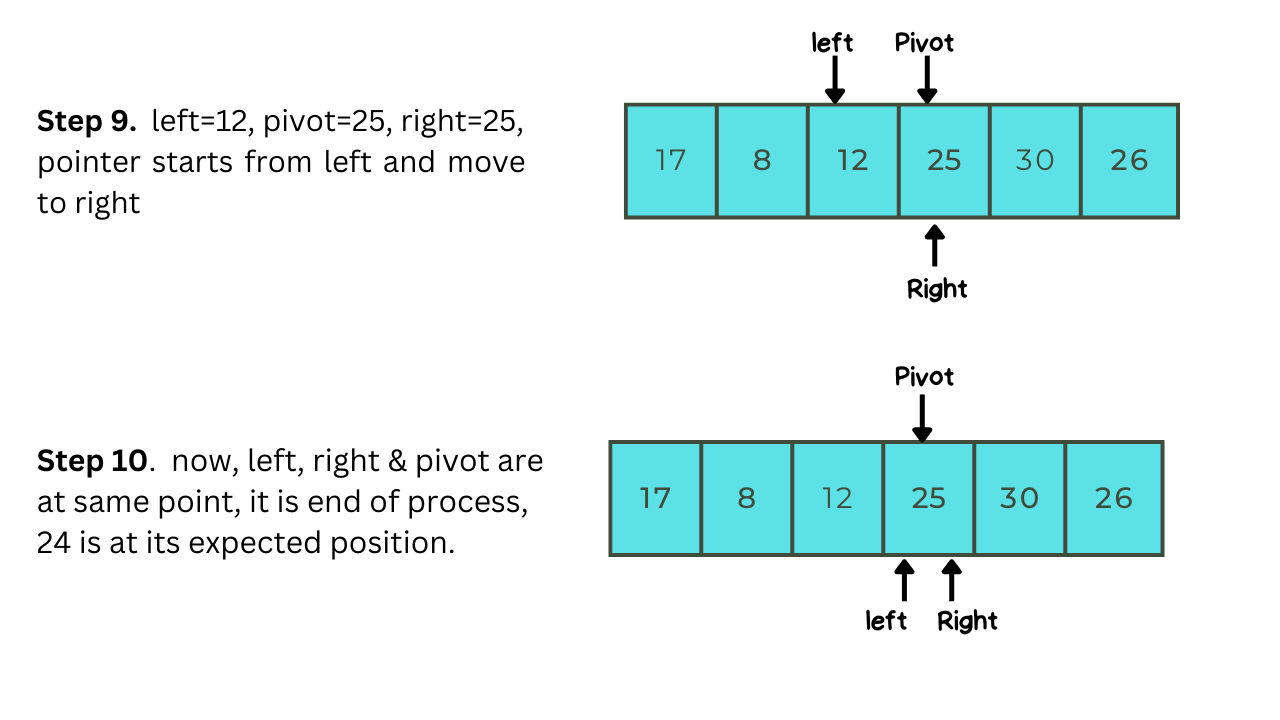
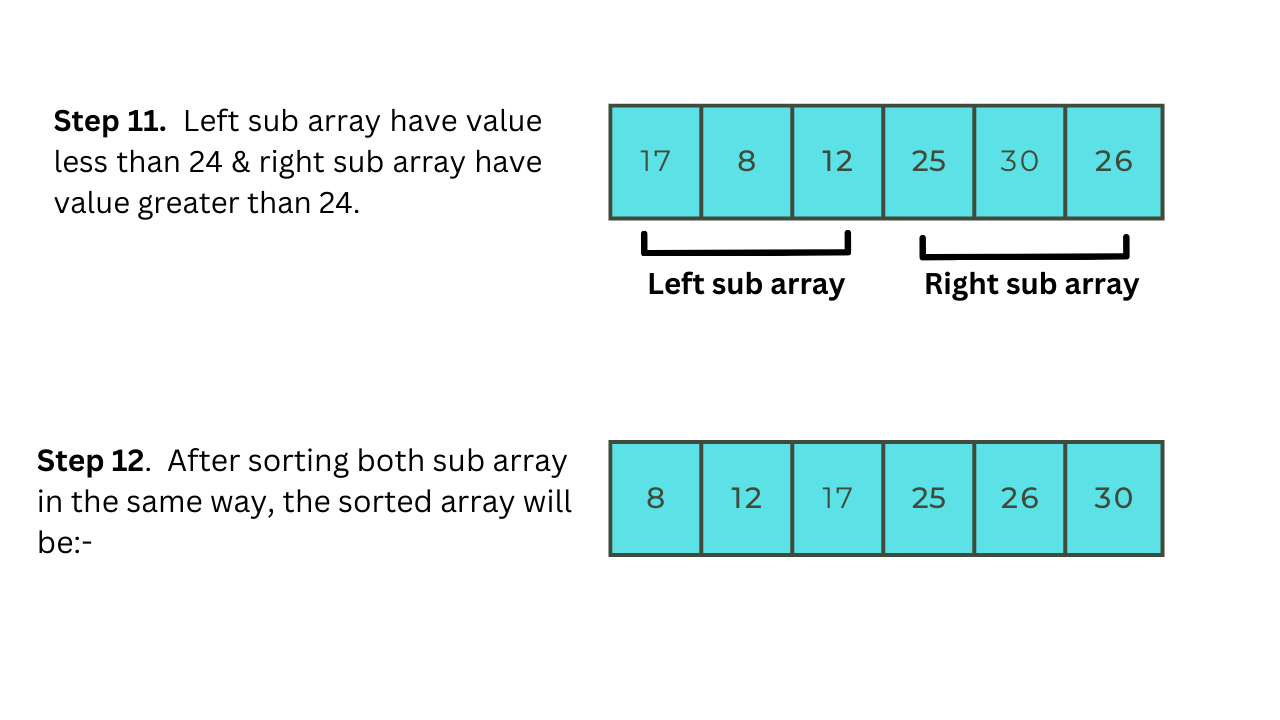

Implementation Of Quick-sort
Here is the Implementation of Quick-sort:
In C++
#include< iostream > using namespace std; // function to swap elements void swap(int *a, int *b) { int t = *a; *a = *b; *b = t; } // function to print the array void printarr(int array[], int size) { int i; for (i = 0; i < size; i++) cout << arr[i] << " "; cout << endl; } // function to rearrange arr (find the partition point) int part(int arr[], int low, int high) { // select the rightmost element as pivot int pivot = arr[high]; // pointer for greater element int i = (low - 1); // traverse each element of the array // compare them with the pivot for (int j = low; j < high; j++) { if (arr[j] <= pivot) { // if element smaller than pivot is found // swap it with the greater element pointed by i i++; // swap element at i with element at j swap(&arr[i], &arr[j]); } // swap pivot with the greater element at i swap(&arr[i + 1], &arr[high]); // return the partition point return (i + 1); } void quickSort (int arr[], int low, int high) { if (low < high) { // find the pivot element such that // elements smaller than pivot are on left of pivot // elements greater than pivot are on righ of pivot int pi = part(arr, low, high); // recursive call on the left of pivot quickSort(array, low, pi - 1); // recursive call on the right of pivot quickSort(arr, pi + 1, high); } } // Driver code int main() { int data[] = {25, 8, 30, 12, 17, 26}; int n = sizeof(data) / sizeof(data[0]); cout << "Unsorted Array: \n"; printArray(data, n); // perform quicksort on data quickSort(data, 0, n - 1); cout << "Sorted array : \n"; printarr(data, n); }
In Python
# function to find the partition position def partition(arr, low, high): # choose the rightmost element as pivot pivot = arr[high] # pointer for greater element i = low - 1 # traverse through all elements # compare each element with pivot for j in range(low, high): if arr[j] <= pivot: # if element smaller than pivot is found # swap it with the greater element pointed by i i = i + 1 # swapping element at i with element at j (arr[i], arr[j]) = (arr[j], arr[i]) # swap the pivot element with the greater element specified by i (arr[i + 1], arr[high]) = (arr[high], arr[i + 1]) # return the position from where partition is done return i + 1 # function to perform quicksort def quicksort(arr, low, high): if low < high: # find pivot element such that # element smaller than pivot are on the left # element greater than pivot are on the right pi = partition(array, low, high) # recursive call on the left of pivot quicksort(arr, low, pi - 1) # recursive call on the right of pivot quicksort(arr, pi + 1, high) data = [25, 8, 30, 12, 17, 26] print("Unsorted Array") print(data) size = len(data) quickSort(data, 0, size - 1) print('Sorted Array :') print(data)
In Java
public class quick
{
/* function that consider last element as pivot,
place the pivot at its exact position, and place
smaller elements to left of pivot and greater
elements to right of pivot. */
int partition (int a[], int start, int end)
{
int pivot = a[end]; // pivot point
int i = (start - 1);
for (int j = start; j <= end - 1; j++)
{
// If current element is smaller than the pivot
if (a[j] < pivot)
{
i++; // increment index of smaller element
int t = a[i];
a[i] = a[j];
a[j] = t;
}
}
int t = a[i+1];
a[i+1] = a[end];
a[end] = t;
return (i + 1);
}
/* function to implement quick sort */
void quick(int a[], int start, int end) /* a[] = array to be sorted, start = Starting index, end = Ending index */
{
if (start < end)
{
int p = partition(a, start, end); //p is partitioning index
quick(a, start, p - 1);
quick(a, p + 1, end);
}
}
/* function to print an array */
void printarr(int a[], int n)
{
int i;
for (i = 0; i < n; i++)
System.out.print(a[i] + " ");
}
public static void main(String[] args) {
int a[] = { 25, 8, 30, 12, 17, 26};
int n = a.length;
System.out.println("\nUnsorted array - ");
Quick q1 = new Quick();
q1.printArr(a, n);
q1.quick(a, 0, n - 1);
System.out.println("\nSorted array- ");
q1.printArr(a, n);
System.out.println();
}
}
Time & Space Complexity of Quick-Sort
Let's examine the time complexity of quicksort in the best, average, and worst case scenarios. We'll also examine quicksort's space complexity.

1. Time Complexity
Best Case Complexity: When the pivot element is always in the middle or very close to the middle element, it happens. The best case complexity is O(n*logn).
Average Case Complexity When the aforementioned prerequisites are not met, it happens. The average case complexity is O(n*logn).
Worst Case Complexity When the largest or smallest element is chosen as the pivot element, it happens. The worst case complexity is O(n2).
This situation results in the situation where the pivot element is located at the very end of the sorted array. A subarray that includes n - 1 elements and another that is always empty. Quicksort is therefore only used on this sub-array.
For distributed pivots, the quicksort method performs better. Quicksort is faster in practise even if its worst-case complexity is higher than that of other sorting algorithms like Merge sort and Heap sort. Quick sort's worst case rarely happens since it may be applied in numerous ways by altering the pivot option. Quicksort's worst case can be solved by selecting the appropriate pivot element.
2. Space Complexity
The space complexity is O(n*logn).
Advantages of Quick-sort
Let's go over a few key advantages of using Quick Sort and several situations when it has been demonstrated to work at its best.
- The above makes it an in-place algorithm since all that is needed is a small auxiliary stack.
- Only n (log n) time is required to sort n objects.
- Its inner loop is only a little bit long.
- You can identify performance difficulties with this algorithm after conducting a comprehensive mathematical analysis of it.
Limitations of Quick-sort
Even though Quick Sort is the fastest algorithm, it has certain drawbacks. Let's talk about some important restrictions you should think about before using real-time Quick Sort.
- It is a repetitive procedure. In particular, if recursion is not given, the implementation is rather difficult.
- It requires quadratic (i.e., n2) time in the worst-case situation.
- It is delicate in that a small implementation mistake could go unnoticed and affect its performance.
Conclusion
This concludes our discussion of "Quick-sort Algorithm". I hope that you gained knowledge about this amazing Algorithm and are now more interested to dive into the DS. You can consult the DATA STRUCTURE Tutorial for further guidance.
Good luck and happy learning!






