 Queue Data Structure in 2025
Queue Data Structure in 2025
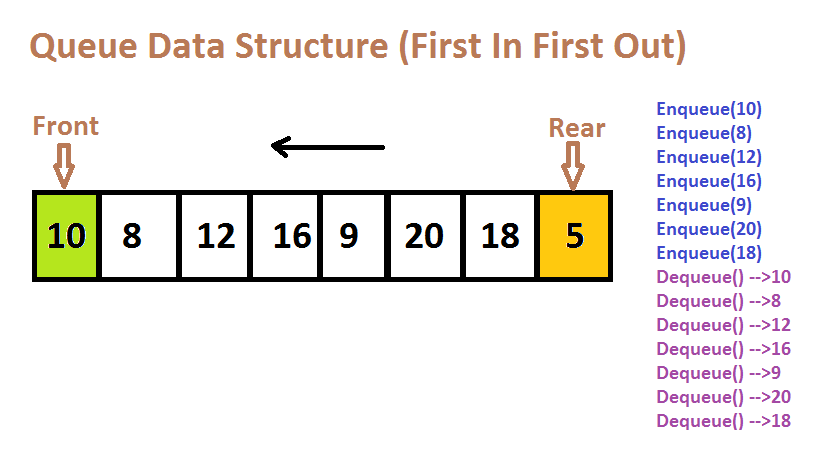

Queue is a data structure that is analogous to a real-world queue. A queue is a data structure that follows the FIFO (First-In-First-Out) policy, in which whatever comes first goes out first. A queue can alternatively be defined as a list or collection in which items are added from one end, referred to as the back end or tail of the queue, and deleted from the other end, referred to as the front end or head of the queue.
The ticket queue outside a cinema hall is a real-world example of a queue, where the person who enters first gets the ticket first, and the person who enters last gets the ticket last. A similar concept is used in the data structure queue.

Arrays, linked lists, pointers, and structures can all be used to create a queue. The use of one-dimensional arrays is the simplest way of all the methods listed.
Elements in the queue, unlike arrays and linked lists, cannot be operated from their separate places. They can only be used at the front and back data pointers. These operations also include conventional methods such as initialising or establishing a data structure, using it, and finally wiping it completely from memory. You should try to understand the operations connected with queues here:
Enqueue() - Elements are added to the queue.
Dequeue() - Element removal from the queue.
Peek() - Without destroying the data element accessible at the front node of the queue, this method acquires it.
isFull() - Checks to see if the queue is full.
isNull() - Checks whether or not the queue is empty.
DSA Courses
• For Coding & System Design Interviews Self-paced Course

Data Structures, Algorithms & System Design(HLD + LLD) in C/C++
Learn From Basic to Advanced DSA, Problem Solving, Scalable System Design (HLD + LLD),Design Patten etc
-

Curriculum
Video Course
-

Duration
Life Time Access
-

Projects,HLD & LLD with real work experience
Learn DSA, System Design,Distributed system & Architecture design, Microservice Architectures, Cloud Technology -

Target Cracking interviews of MAANG and Top Product based companies
Language : Java, Python & C++
Course Fee : 4,000/-
• For Coding Interviews Self-paced Course

Data Structures, Algorithms & Problem Solving in C/C++
Learn From Basic to Advanced Data Structures, Algorithms & Problem-Solving techniques
-

Curriculum
Video Course
-

Duration
Life Time Access
-

Professional Projects to learn with real work experience
Learn Data Structures, Algorithms, OOPS concepts, Problem solving skills and Projects based on it -

Target Cracking interviews of MAANG and Top Product based companies
Language : Java, Python & C++
Course Fee : 3,000/-

Queue Data Structure in 2025
⌚ What are queues in data structure?
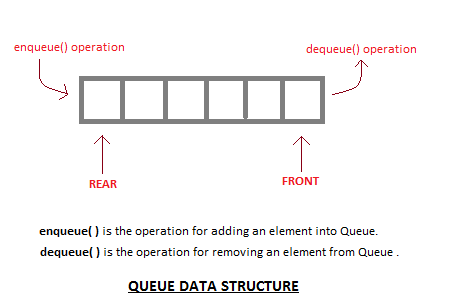
Queues are programmed data structures that only enable access to the first item inserted at a time. Internally, queue data structure are implemented using different data structures such as arrays. Because the first item inserted is the first to be withdrawn, a queue is a First-In-First-Out (FIFO) storage method.
Enqueue is the process of adding an element to a queue, while Dequeue is the process of removing an element from a queue.
⌚List some real-world Queue uses.
Like the name implies, a queue is employed whenever we need to handle a set of items in such a way that the first one in comes out first while the others wait in line, as in the following scenarios:
Requests are served from a single shared resource, such as a printer, and CPU tasks are scheduled, among other things.
In the real world, Call Center phone systems use Queues to keep people who call in order until a service person is available.
Interrupt handling in real-time systems. Interrupts are dealt with in the order in which they are received, i.e. first come, first served.
⌚What is Queue Operations Complexity Analysis?
By moving the initial piece off the front of the line, queues provide random access to their contents. You must repeat this process in order to access an arbitrary element in the queue. Therefore, access is O(n).
Iterating until you discover a specific value in the queue is required while searching for it. As a result, search is O. (n).
By definition, inserting into a queue can only happen at the back of the line, comparable like standing in line at In 'n Out for a scrumptious Double-Double burger. Queue insertion is O in the case of an efficient queue implementation (1).
The process of deleting items from a queue occurs at the front of the line. Queue deletion is 'O' in the case of an efficient queue implementation (1).
⌚What are types of Queue in Data Structure?
The following are the different types of queues:
Simple Queue - It is a linear data structure in which elements are deleted in the same order that they were introduced, i.e. the element that was inserted first is removed first.
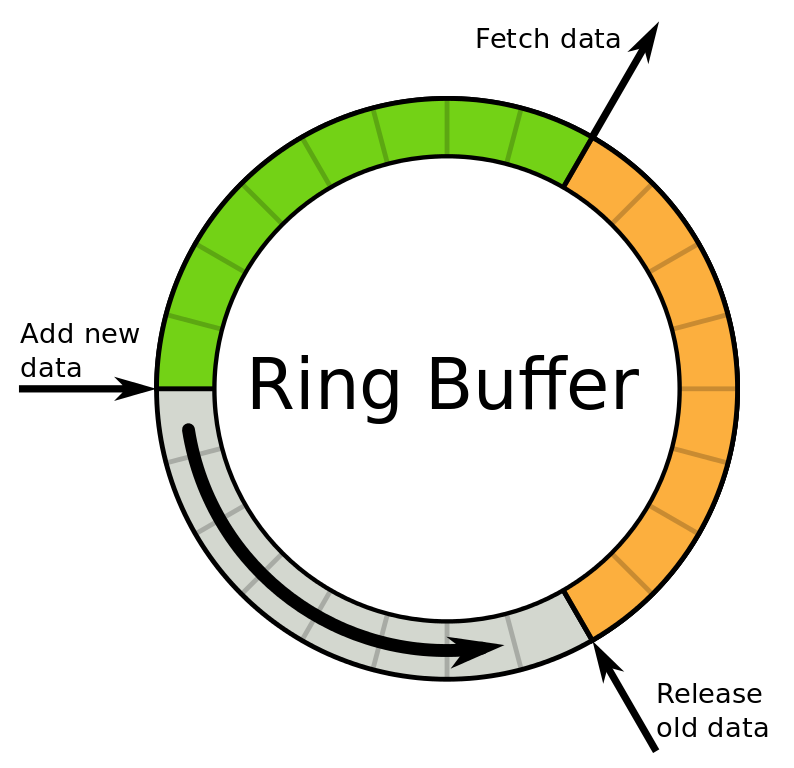
Circular Queue - It's a linear data structure in which operations are carried out according to the FIFO (First In, First Out) principle, and the last place is connected to the first to form a circle. Ring Buffer is another name for it. A circular queue avoids the waste of space that occurs when utilising arrays in a standard queue implementation.
Priority Queue - It's a sort of queue in which each element has a priority value, and the priority value determines whether or not the elements are deleted.
In a max-priority queue, the element with the highest priority value is destroyed first.
When using a min-priority queue, the element with the lowest priority value will be destroyed first.
De-queue (Double ended queue) - It supports insertion and deletion from both ends, allowing elements to be added or removed from both the backend and the frontend.
⌚ What are the main public interfaces that queues provide?
The following are the most common interfaces provided by queues.
🚀 insert() - Adds a new data item to the queue's end.
🚀 remove() - Removes the item from the queue's end.
🚀 peek() - The item is returned to the front of the queue without being removed.
🚀 isFull() - If the queue is full, this method returns true.
🚀 isEmpty() - If the queue is empty, this method returns true.
⌚Create a program that implements queue functionality?
The queue feature is implemented in the Java programme below. The implementation is done internally using an array.
class MyQueue { private int maxSize; private int[] queueArray; private int front; private int rear; private int numberOfItems; //constructor public MyQueue(int maxSize) { this.maxSize = maxSize; queueArray = new int[maxSize]; front = 0; rear = -1; numberOfItems = 0; } //insert an item to queue public void insert(int i) { //increment rear and insert item queueArray[++rear] = i; nItems++; } //remove an item from queue public int remove() { //return item and decrement top int temp = queueArray[front++]; nItems--; return temp; } //view item from top of stack public void peek() { return queueArray[front]; } //check if stack is empty public void isEmpty() { return (numberOfItems== -1); } //check if stack is full public void isFull() { return numberOfItems == maxSize); } }
⌚Why should I use Stack or Queue data structures instead of Arrays/Lists, and when should I use them?
Because they assist you in managing your data in a more specific manner than arrays and lists. It means you won't have to wonder if someone placed an element in the midst of your list at random, messing up certain invariants when troubleshooting an issue.
Random access is the nature of arrays and lists. They're incredibly adaptable, but they're also easily corruptible. It's recommended to use those already developed collections if you wish to manage your data like FIFO or LIFO.
In terms of practicality, you should:
When you want to get items out in the same order that you put them in, use a queue (FIFO)
When you need to get things out in the opposite order that they were put in, use a stack (LIFO)
When you need to get anything out, regardless of when you put it in (and when you don't want it to be automatically removed), use a list.
⌚What exactly are Deques?
Deques are double-ended queues in which you can add items from the front or the back, and delete items from either the front or the back. To insert and remove from both ends, Deques provide methods equivalent to insertLeft(), insertRight(), removeLeft(), and removeRight().
⌚What are Priority Queues and How Do They Work?
A priority queue is a customised queue in which the items are sorted by lowest (or highest) key. As a result, when you obtain an item from a priority queue, you always get the item with the lowest value (or highest value item based on how the items are ordered).
⌚Write a program that implements the priority queue feature?
The priority queue functionality is implemented using the Java programme below. The implementation is done internally using an array. The array items are sorted ascending, and the insert() function places an item in the correct place in the array.
class MyPriorityQueue { private int maxSize; private int[] queueArray; private int numberOfItems; //constructor public MyPriorityQueue(int maxSize) { this.maxSize = maxSize; queueArray = new int[maxSize]; numberOfItems = 0; } //insert an item to queue public void insert(int i) { //increment rear and insert item if(numberOfItems==0){ queueArray[numberOfItems] = i; } else { for(int j=numberOfItems-1; j>=0; j--) { if(i > queueArray[j]) { queueArray[j+1] = queueArray[j]; } else { break; } } queueArray[++rear] = i; nItems++; } } //remove an item from queue public int remove() { //return item and decrement count return queueArray[--numberOfItems]; } //view item from top of stack public void peek() { return queueArray[numberOfItems-1]; } //check if stack is empty public void isEmpty() { return (numberOfItems == 0); } //check if stack is full public void isFull() { return (numberOfItems == maxSize); } }
⌚ What is the difference between a queue and a stack of items?
| Parameter | Stack Data Structure | Queue Data Structure |
| Basics | It's a data structure that's linear. At the same end, the objects are removed or placed. | It's also a data structure that's linear. The objects are taken out and put back in from two distinct angles. |
| Working Principle | The idea of LIFO (Last In, First Out) is followed. It signifies that the most recently added part is removed first. | The principle of First In, First Out (FIFO) is followed. It signifies that the first piece added to the list is eliminated first. |
| Pointers | It just has one pointer, which is at the top. The address of the stack's topmost element, or the last inserted one, is indicated by this pointer. | It reads and writes data from both ends—the front and the back—using two pointers (in a simple queue). The address of the final inserted element is indicated by the back pointer, whereas the address of the first inserted element in a queue is indicated by the front pointer. |
| Operations | Push and pop are two of Stack's operations. The pop operation is used to remove an element from a list, whereas the push operation is used to add an element to one. | Enqueue and dequeue are two of Queue's operations. The dequeue operation removes elements from a queue, whereas the enqueue operation adds them to one. |
| Structure | Only one end of the element is used for insertion and deletion. The top is what it's called. | It has two ends, one in the front and one in the back. The back end is used for insertion, and the front end is used for deletion. |
| Full Condition Examination | When top==max-1, the stack has reached its maximum capacity. | When rear==max-1, it means that the queue is full. |
| Empty Condition Examination | It signifies that the stack is empty when top==-1. | It shows that the queue is empty when front = rear+1 or front== -1. |
| Variants | There are no types in a Stack data structure. | There are three types of queue data structures: circular queue, priority queue, and double-ended queue. |
| Visualization | The Stack can be viewed as a vertical collection. | A Queue can be thought of as a horizontal collection. |
| Implementation | In a Stack, the implementation is easier. | In comparison to a stack, the implementation of a Queue is more sophisticated. |
⌚ What are some basic features of queue data structure?
🚀 A queue, like a stack, is an ordered list of elements of comparable data types.
🚀 The structure of a queue is FIFO (First in First Out).
🚀 To remove a new element from the Queue, all elements entered before the new element in the queue must be removed.
🚀 The peek() function is frequently used to get the first element's value without dequeuing it.
⌚ What are the applications of priority Queue?
The priority queue has the following applications:
The shortest path algorithm of Dijkstra is based on it.
Prim's algorithm makes advantage of it.
It's utilised in Huffman code and other data compression techniques.
It's a sorting algorithm that's employed in heaps.
Priority scheduling, load balancing, and interrupt management are all examples of how it is utilised in operating systems.
⌚ What is a Circular Queue, and how does it work?
A circular queue is similar to a linear queue in that it is based on the FIFO (First In First Out) concept, except that in a circular queue that forms a circle, the last position is connected to the first position. A Ring Buffer is another name for it.
⌚Why was the circular queue concept introduced?
There was one drawback to Queue's array implementation. If the back of the line reaches the end of the line, there is a chance that some empty spaces will be left at the beginning of the line that will not be filled. As a result, the notion of the circular queue was developed to address these limits.
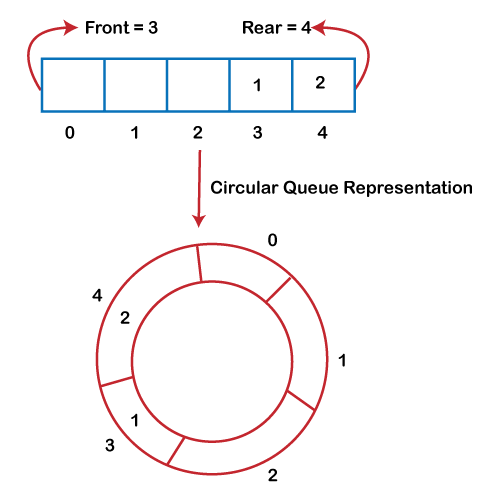
The rear of the queue is at the last position, and the front is pointing somewhere other than the 0th position, as shown in the above image. There are just two elements in the above array, and the remaining three positions are vacant. The back is at the end of the Queue; attempting to insert the element will reveal that there are no empty spaces in the Queue. There is a way to prevent wasting memory by relocating both parts to the left and adjusting the front and back ends accordingly. It is not a realistic approach because rearranging all of the pieces will take a long time. The most effective way to prevent wasting resources
⌚ What are the applications of circular Queue?
In the following cases, the circular queue can be used:
Memory management: Memory management is provided by the circular queue. The memory is not managed particularly efficiently in linear queue, as we have already shown. In the case of a circular queue, however, memory is efficiently handled by placing the elements in an unused area.
CPU Scheduling: The circular queue is also used by the operating system to insert and execute processes.
Traffic system: The traffic light is one of the best instances of the circular queue in a computer-controlled traffic system. After every j interval of time, each traffic light turns on one by one. For example, a red light will turn on for one minute, then a yellow light will turn on for one minute, and then a green light will turn on for one minute. The red light turns on after the green light.
⌚What is double ended queue in data structure?
Deque is another name for a double-ended queue. The insertion and deletion of an element can happen at both ends of this queue. Deque is further separated into two types:-
Input Restricted Deque :- In this case, input is limited at one end but deletion is allowed at both ends.
Output Restricted Deque :- In this case, output is blocked at one end while insertion is allowed at both ends.
⌚What are the applications of double ended queue?
The following are some examples of double ended queue applications:
Undo and redo operations are performed.
For the purpose of implementing stacks.
Keeping track of online browser history.
⌚ How can you use JAVA programming to add an element to a Queue?
Insertion in a queue in java is a simple operation that we can perform on Queue Data Structure. Insertion in a Queue is also known as Enqueue operation when we are talking in respect with Queues.
The processes to fill an empty queue whose size and data will be determined by user input will be discussed here.
We'll use the queue size as user input in the main function.
Then we'll create a for loop that will iterate until the queue is full.
On each cycle, we will request data from the user and use the enqueue function to insert that data into the queue.
On each successful repetition, we shall increase the value of rear by one in the enqueue function.
Later on, we'll utilise the display method to show the data that's in the queue.
import java.util.Scanner; public class Main { public final static int MAX = 50;/*Defining the max size of the queue*/ public static int[] queue = new int[MAX]; public static int front = -1, rear = -1; public static void enqueue(int data) /* function to enqueue data */ { if(rear == MAX - 1) { System.out.print("\nQueue is Full!"); } else { rear = rear + 1; queue[rear] = data; if(front == -1) { front = 0; } } } public static void disp() /* function to display the elements of the queue */ { System.out.print("\nThe elements in the queue are:"); if(front == -1) { System.out.print("\nQueue is Empty"); } else { for(int i = front; i <= rear; i++) { System.out.print(queue[i] + " "); } } System.out.println(); } public static void main(String[] args) /* main function for all input and output statements */ { int data, size; System.out.print("Enter the size of queue: "); size = STDIN_SCANNER.nextInt(); for(int i = 0; i < size; i++) { System.out.println("\nEnter Data to Enqueue:"); data = STDIN_SCANNER.nextInt(); System.out.println("Enqueuing " + data); enqueue(data); disp(); } } public final static Scanner STDIN_SCANNER = new Scanner(System.in); }
⌚ In JAVA programming, how do you delete an element from a queue?
In Java, deletion occurs from the front of the queue because Queue follows the FIFO principle, which states that the element that is added first will be the first to be deleted. Dequeue refers to the process of removing an item from a queue.
The procedures below are used to erase data from a queue that is currently being dequeued.
Check the front position; if the front is at -1 or rear+1, the queue is empty.
Otherwise, move the front one position forward.
To see the data, use the display function.
Check if the queue has any data in that display function once more.
If the queue contains data, use a for loop to display the data that remains after dequeuing.
import java.util.Scanner; public class Main { public final static int MAX = 50;//defining max size of queue public static int[] queue = new int[MAX]; public static int front = -1, rear = -1; public static void enqueue(int data) /* function to enqueue data */ { if(rear == MAX - 1) { System.out.print("\nQueue is Full!"); } else { rear = rear + 1; queue[rear] = data; if(front == -1) { front = 0; } } } public static void disp() /* function to display the relents of the queue */ { System.out.print("\nThe elements in the queue are:"); if(front == -1) { System.out.print("\nQueue is Empty"); } else { for(int i = front; i <= rear; i++) { System.out.print(queue[i] + " "); } } System.out.println(); } public static void dequeue() /* function to delete elements from the queue */ { if(front == -1 || front == rear + 1) { System.out.print("\nQueue is Empty"); } else { queue[front] = 0; front = front + 1; } disp(); } public static void main(String[] args) /* main function for all input and output statements */ { int data, size; System.out.print("Enter the size of queue:"); size = STDIN_SCANNER.nextInt(); System.out.println("\nEnter Data to Enqueue:"); for(int i = 0; i < size; i++) { data = STDIN_SCANNER.nextInt(); enqueue(data); } disp(); System.out.println("\nDequeuing:"); { dequeue(); } } public final static Scanner STDIN_SCANNER = new Scanner(System.in); }
⌚ In the Java programming language, how do you reverse a queue?
Following are the steps to reverse a queue:
We'll start by making a Queue.
Take input from the user to start the Queue.
Make a call to the reverse function.
The stack might be useful in approaching this issue. There will be two steps to this:
Insert the elements from the queue onto the stack. (The queue's last element is the topmost element of the stack.)
To re-enter the queue, pop the items of the stack. (The last piece in the queue is the first to be added.)
To print the data, use the show function.
import java.util.LinkedList; import java.util.Queue; import java.util.Stack; public class Main { static Queue<Integer> que; static void show() { while (!que.isEmpty()) { System.out.print( que.peek() + “, “); que.remove(); } } // Function to reverse the que static void queuereverse() { Stack<Integer> stk = new Stack<>(); while (!que.isEmpty()) { stk.add(que.peek()); que.remove(); } while (!stk.isEmpty()) { que.add(stk.peek()); stk.pop(); } } // Driver code public static void main(String args[]) { que = new LinkedList<Integer>(); que.add(5; que.add(20); que.add(60); que.add(40); queuereverse(); show(); } }
⌚How to implement Queue using Linked List?
A linked list can easily be used to create a queue. The enqueuing of items occurs at the tail of the list, and the dequeuing of items occurs at the head of the list in a singly linked list implementation. To keep insertion O(1) efficient, we need to hold a pointer to the last node.
Use a doubly linked list if we want enqueuing to happen at the start and dequeuing to happen at the conclusion of the linked list because it offers O(1) insertion and deletion on both ends.
// A Linked List Node class Node { int data; // integer data Node next; // pointer to the next node public Node(int data) { // set data in the allocated node and return it this.data = data; this.next = null; } } class Queue { private static Node rear = null, front = null; private static int count = 0; // Utility function to dequeue the front element public static int dequeue() // delete at the beginning { if (front == null) { System.out.println("\nQueue Underflow"); System.exit(-1); } Node temp = front; System.out.printf("Removing %d\n", temp.data); // advance front to the next node front = front.next; // if the list becomes empty if (front == null) { rear = null; } // decrease the node's count by 1 count -= 1; // return the removed item return temp.data; } // Utility function to add an item to the queue public static void enqueue(int item) // insertion at the end { // allocate a new node in a heap Node node = new Node(item); System.out.printf("Inserting %d\n", item); // special case: queue was empty if (front == null) { // initialize both front and rear front = node; rear = node; } else { // update rear rear.next = node; rear = node; } // increase the node's count by 1 count += 1; } // Utility function to return the top element in a queue public static int peek() { // check for an empty queue if (front == null) { System.exit(-1); } return front.data; } // Utility function to check if the queue is empty or not public static boolean isEmpty() { return rear == null && front == null; } // Function to return the size of the queue private static int size() { return count; } } class Main { public static void main(String[] args) { Queue q = new Queue(); q.enqueue(1); q.enqueue(2); q.enqueue(3); q.enqueue(4); System.out.printf("The front element is %d\n", q.peek()); q.dequeue(); q.dequeue(); q.dequeue(); q.dequeue(); if (q.isEmpty()) { System.out.println("The queue is empty"); } else { System.out.println("The queue is not empty"); } } }
⌚ How to implement Queue using Stack?
For constructing a queue, we can utilise both an implicit stack (call stack) and a real stack. All components from the stack are popped and stored in the call stack by the dequeue process. Remove and return a single item from the stack when it's all that's left. Finally, as the recursion progresses, push all pieces from the call stack back into the stack.
import java.util.Stack; // Implement a queue using a single stack class Queue<T> { private Stack<T> s; // Constructor Queue() { s = new Stack<>(); } // Add an item to the queue public void enqueue(T data) { // push item into the first stack s.push(data); } // Remove an item from the queue public T dequeue() { // if the stack is empty if (s.isEmpty()) { System.out.println("Underflow!!"); System.exit(0); } // pop an item from the stack T top = s.pop(); // if the stack becomes empty, return the popped item if (s.isEmpty()) { return top; } // recur T item = dequeue(); // push popped item back into the stack s.push(top); // return the result of dequeue() call return item; } } class Main { public static void main(String[] args) { int[] keys = { 1, 2, 3, 4, 5 }; Queue<Integer> q = new Queue<Integer>(); // insert the above keys into the queue for (int key: keys) { q.enqueue(key); } System.out.println(q.dequeue()); // print 1 System.out.println(q.dequeue()); // print 2 } }
⌚ Which data structures are used in the LRU cache implementation?
The LRU cache, or Least Recently Used cache, organises objects in order of use to make it easier to find an element that hasn't been used in a long time. Two data structures are utilised to do this:
Queue – A doubly-linked list is used to do this. The cache size, i.e. the total number of available frames, determines the queue's maximum size. The pages that have been used the least lately will be near the front of the queue, while the pages that have been used the most recently will be near the back.
Hashmap – The page number is the key, and the address of the matching queue node is the value, in a hashmap.
⌚What are the five basic queue operations?
Basic Queue Operations
Enqueue: Add a new element to the queue's end.
Dequeue: Remove an element from the queue's front.
IsEmpty: Make sure the queue isn't full.
IsFull: Check to see if the queue is already full.
Peek: Get the front of the queue's value without removing it.
⌚ What is the difference between a max and a min-priority queue?
The element with the largest key is returned first in a max-priority queue, while the element with the smallest key is returned first in a min-priority queue. Many algorithms, such as Huffman Codes and Prim's algorithm, use priority queues. It's also utilised in computer scheduling, among other things.
⌚What do the terms "front" and "back" in a queue mean?
A queue is an ordered collection of items in which new items are added at one end, referred to as the "back," and current items are removed at the other end, referred to as the "front." When an element joins the queue, it begins at the back and works its way to the front, waiting to be the next element to be removed.
⌚ What's the Difference Between a Circular and a Linear Queue?
🚀 The major difference between a linear queue and a circular queue is that a linear queue arranges data in a linear fashion, one after the other, but a circular queue arranges data in a circular fashion by connecting the last element to the first one.
🚀 It is possible to add new items from the back and remove items from the front in a linear queue. In a circular queue, however, elements can be added and removed from any position. Hence, this is another difference between linear queue and circular queue.
🚀 Another distinction between the linear and circular queues is memory space. The memory requirements for a linear queue are higher than for a circular queue.
🚀 Another distinction between the linear and circular queues is efficiency. In comparison to a linear queue, a circular queue is more efficient.
⌚What happens if the peek () action is done in a queue?
Queue Interface's peek() method returns the element at the front of the container. The element in the container is not deleted. The head of the queue is returned by this procedure. When the Queue is empty, the procedure returns null rather than throwing an exception.
Syntax:
E peek()
This method returns the Queue's head; if the Queue is empty, it returns false.
⌚ What are the benefits of using a queue in a data structure?
Following are some of the benefits of using queue data structure:
🚀 Multiple Clients : While queues are more complicated than stacks, the array simplifies them by placing the most recent member at the end and advancing each element one step forward when one item of data is taken from the queue. Queues are useful when several customers are involved in the same procedure. A website, for example, may only have so much capacity to allow customers to download a specific file. With a stack, some customers may have to wait considerably longer than the newest customers to get the file. Queues are also useful when the data is not received by the client at the same time it is sent.
🚀 Circular Queues : Because a larger array is required than the entire number of pieces of data, queues can result in empty spaces in the data structure. Programmers, on the other hand, can make use of the empty space by using circular queues. Time outs can be specified by programmers to make jobs wait until the input reaches the data queue.
🚀 Speed : Data queues are a quick way to communicate between processes. Data queues free up jobs from doing particular tasks, resulting in faster response times and greater overall system performance. Data queues are the quickest way to communicate asynchronously between two activities because they have less overhead than database files and data regions.
🚀 Flexibility : Queues are adaptable and don't require any communication programming. Inter-process communication is not required knowledge for the programmer. Computers can manage several jobs thanks to data queues. When there are no entries in the queue, it can remain active, ready to handle data entries as needed.
🚀 Multiple Jobs : Because some processes have performance constraints and are unable to handle all of the entries, the data is divided among numerous jobs. Because only one customer service representative may assist a customer at a time, the queue can distribute customer service requests across agents, allowing for faster processing.
🚀Conclusion
We have now reached the end of this page. With the knowledge from this page, you should be able to create your own programmes with some research, and it's in fact recommended to hone your programming skills with small projects. There is no way to cover all the information you need to be a successful programmer in one course. In fact, programming is a constant learning process, regardless of whether you are a seasoned professional developer or a newbie.
Good luck and happy learning!
Frequently Asked Questions (FAQs)
In data structures, a queue is an abstract data type that follows the First-In-First-Out (FIFO) principle. It represents a collection of elements where the element that is inserted first is the first one to be removed. It operates similar to a real-world queue or line, where the first person to enter the queue is the first one to exit.
A queue has two main operations: enqueue and dequeue. Enqueue refers to adding an element to the end of the queue, while dequeue refers to removing the element from the front of the queue.
These operations are performed in a sequential manner, maintaining the order of insertion.
Here's a step-by-step explanation of the main operations and characteristics of a queue:
1. Enqueue: This operation adds an element to the end (rear) of the queue. The new element becomes the last element in the queue. If the queue is empty, the new element becomes both the first and last element.
2. Dequeue: This operation removes the element from the front (head) of the queue. The element that was first inserted is the one to be removed. After removal, the next element in line becomes the new front element.
3. Front: It refers to the element at the front of the queue, which is the next element to be dequeued.
4. Rear: It refers to the element at the end of the queue, which is the last element that was enqueued.
5. Empty Queue: A queue is said to be empty when it contains no elements. In this state, both the front and rear pointers are null or point to a sentinel value.
6. Full Queue: In some implementations, a queue may have a fixed size, and when it reaches that size, it is considered full and no more elements can be enqueued. However, in other implementations, a queue can dynamically grow in size to accommodate more elements.
7. Peek: This operation allows you to examine the element at the front of the queue without removing it. It provides a way to access the first element without altering the queue's state.
Queues are commonly used in situations where elements need to be processed in the order they arrive. Some examples of real-life scenarios where queues are used include:
- Simulating real-world systems: Queues can model various systems where entities enter and exit, such as a ticketing system, customer support system, or task scheduling system.
- CPU scheduling: In operating systems, queues are used to manage the execution of processes or threads, ensuring fairness and maintaining order.
- Breadth-First Search: Queues are utilized in graph algorithms like Breadth-First Search (BFS) to explore adjacent vertices layer by layer.
- Print spooling: In printing systems, queues are used to manage the order of print jobs, ensuring that they are processed in the order they were requested.
There are several variations of queues, such as circular queues and priority queues, each designed to cater to specific requirements. Queues provide an efficient and organized way to manage elements in a sequential order, making them a fundamental data structure in computer science and software development.
An example of a queue data structure can be a printer spooler system. Let's consider a scenario where multiple users are sending print requests to a printer. The printer has limited resources and can process one print request at a time. In such a situation, a queue data structure can be used to manage the print requests and ensure that they are processed in the order they are received.
Here's how the queue data structure can be applied in this example:
1. Enqueue: When a user sends a print request, it is added to the end of the queue. Each print request becomes an element in the queue, representing the order in which the requests were received. The newest request is added to the rear of the queue.
2. Dequeue: The printer can only process one print request at a time. When the printer is ready to process a request, the front element of the queue is dequeued. This means that the first print request in the queue is removed and sent to the printer for processing. The next request in line becomes the new front element and is ready to be dequeued when the printer is available.
3. Front: The front of the queue represents the print request that is currently being processed or is next in line to be processed. It is the element that will be dequeued when the printer is ready.
4. Rear: The rear of the queue represents the most recent print request that was added to the queue. It is the element that will be dequeued last, as it represents the print request that was received most recently.
5. Empty Queue: If there are no print requests in the queue, it means the queue is empty. This occurs when all the print requests have been processed, and there are no pending requests in line. In this case, both the front and rear pointers of the queue will be null or point to a sentinel value.
The printer spooler system is an example of how a queue data structure can be used to manage a sequence of tasks or events that need to be processed in a specific order. By implementing a queue, the printer can ensure fairness and process print requests in the order they were received, following the FIFO principle.
It's worth noting that this is just one example of how a queue data structure can be used. Queues have various applications in computer science and real-world scenarios where managing sequential data is necessary. Other examples include task scheduling systems, message queues in software applications, and network packet routing algorithms. The flexibility and simplicity of queues make them a powerful tool for organizing and managing data in a wide range of scenarios.
There are several variations of queues that can be used in different scenarios. Here are four commonly used types of queues:
1. Simple Queue: A simple queue is the basic form of a queue. It follows the First-In-First-Out (FIFO) principle, meaning that the element that is inserted first is the first one to be removed. Elements are added to the rear (end) of the queue and removed from the front (head) of the queue. It maintains the order of insertion and retrieval.
2. Circular Queue: A circular queue, also known as a ring buffer, is a variation of the simple queue that overcomes the limitation of linear queues, where the rear and front can reach the end of the underlying array. In a circular queue, the rear and front pointers wrap around to the beginning of the queue when they reach the end. This allows efficient space utilization and allows the queue to be used in a fixed-size buffer. Circular queues are often implemented using an array or a circular linked list.
3. Priority Queue: A priority queue is a type of queue where each element is assigned a priority value. Elements with higher priority are dequeued first. This differs from a simple queue, where elements are dequeued based on their order of insertion. Priority queues can be implemented using various data structures such as arrays, binary heaps, or binary search trees. They are useful in scenarios where elements have different priorities and need to be processed accordingly.
4. Double-ended Queue (Deque): A double-ended queue, also known as a deque, is a queue that allows insertion and deletion at both ends. Elements can be added or removed from either the front or the rear of the queue. This provides flexibility in managing the order of elements. Deques can be used to implement both stacks and queues. They can be implemented using arrays or linked lists.
Each type of queue has its own advantages and use cases:
- Simple queues are used when elements need to be processed in the order they arrive, following the FIFO principle.
- Circular queues are useful in scenarios where there is a fixed-size buffer or when efficient space utilization is desired.
- Priority queues are ideal when elements have different priorities and need to be processed based on their priority levels.
- Deques are versatile data structures that allow insertion and deletion at both ends, making them suitable for various scenarios where flexibility in managing the order of elements is required.
Understanding the different types of queues allows you to choose the appropriate data structure based on the requirements of your specific problem or application. By selecting the right type of queue, you can efficiently manage and process data in a way that meets the needs of your application.
The term FIFO stands for "First-In-First-Out," and it is used to describe the fundamental behavior of a queue data structure. A queue follows the FIFO principle, which means that the element that is inserted first into the queue is the first one to be removed. This behavior is similar to how people line up in a queue or waiting line in real-life scenarios.
Here's a detailed explanation of why a queue is called FIFO:
1. First-In: When elements are added to a queue, they are inserted at the rear (end) of the queue. The first element to be inserted is placed at the rear, becoming the first element in the queue. As more elements are added, they are placed one after another in the queue, maintaining the order of insertion.
2. First-Out: When it comes to removing elements from the queue, the element at the front (head) of the queue is the first one to be removed. This element represents the oldest or the earliest element in the queue since it was inserted first. Once the element is dequeued, the next element in line becomes the new front, ready to be dequeued next.
The concept of FIFO is derived from real-life scenarios where people wait in a line or queue for a service, such as standing in line at a ticket counter, waiting for a bus, or getting served at a restaurant. In these situations, the person who arrives first is the first one to be served or attended to. The same principle applies to a queue data structure.
The FIFO behavior of a queue is crucial in many practical scenarios, including managing processes in an operating system, handling network packets, implementing message queues in software applications, and simulating real-world systems where entities enter and exit in a specific order.
By following the FIFO principle, queues ensure fairness and maintain the chronological order of elements. This behavior allows applications to process data or tasks in the same order they were received, ensuring that elements are handled in a systematic and organized manner.
Overall, the term FIFO accurately describes the behavior of a queue data structure, where the first element to enter is the first one to be removed, replicating the natural order observed in real-life queues.
Queues have a wide range of applications across various domains due to their ability to manage and process data in a specific order. Here are six common applications of queues:
1. Process Scheduling: In operating systems, queues are used to schedule and manage processes or tasks. Different queues may be used to prioritize tasks based on their urgency or importance. For example, a priority queue can be used to give higher priority to critical tasks, ensuring they are processed promptly.
2. Print Spooling: Queues are commonly used in print spooling systems. When multiple print requests are received, they are added to a print queue. The printer processes the requests one by one in the order they were received. This ensures fair access to the printer and maintains the order of printing.
3. Web Server Request Handling: Web servers often use queues to handle incoming requests from clients. Each incoming request is added to a request queue, and the server processes the requests sequentially. This ensures that requests are processed in the order they arrive, preventing any request from being neglected or delayed.
4. Network Packet Routing: In network communication, queues are used for packet routing. Routers and switches use queues to hold packets temporarily before forwarding them to their destination. The packets are processed based on their arrival order, ensuring fairness and avoiding congestion.
5. Task Management in Multitasking Systems: Queues are essential in managing tasks in multitasking systems. Each task is added to a task queue, and the system scheduler determines the order in which tasks are executed. By following the FIFO principle, queues ensure that tasks are executed in the order they were initiated.
6. Message Queues in Software Applications: Queues are widely used in software applications for asynchronous communication and handling of messages. Message queues allow different components or modules of an application to exchange information in a decoupled manner. Messages are placed in a queue and processed by the receiver when it is ready. This helps manage the flow of information and allows components to operate at their own pace.
These are just a few examples of how queues are applied in various domains. Queues offer a simple and effective way to manage data and tasks in a sequential manner, ensuring fairness, maintaining order, and enabling efficient processing. Their versatility and efficiency make them a valuable tool in many applications where data or tasks need to be organized and processed in a specific order.
A queue algorithm refers to a set of procedures or steps designed to manipulate and operate on a queue data structure. It outlines the operations and rules for inserting and removing elements from the queue while maintaining the FIFO (First-In-First-Out) order.
The key operations involved in a queue algorithm include:
1. Enqueue: This operation adds an element to the rear (end) of the queue. It involves inserting the element at the appropriate position to maintain the order of insertion. If the queue is empty, the element becomes both the front and rear element.
2. Dequeue: This operation removes the element from the front of the queue. It follows the FIFO principle, meaning that the first element that was inserted is the first one to be removed. After dequeuing an element, the next element in line becomes the new front element.
3. Front: This operation retrieves the element at the front of the queue without removing it. It allows accessing the next element to be dequeued.
4. Rear: This operation retrieves the element at the rear of the queue without removing it. It provides access to the last element that was enqueued.
5. IsEmpty: This operation checks whether the queue is empty or not. It returns a boolean value (true or false) indicating the status of the queue.
6. IsFull: In some implementations, this operation checks whether the queue is full or has reached its maximum capacity. It is applicable when using a fixed-size array or buffer to store the queue elements.
The queue algorithm ensures that elements are inserted and removed in the correct order, maintaining the integrity of the data structure. It enforces the rules of the queue and prevents elements from being inserted in the middle or removed from locations other than the front.
Implementations of the queue algorithm can vary depending on the programming language and the underlying data structure used to represent the queue. Common data structures used to implement queues include arrays, linked lists, and dynamic arrays.
The queue algorithm is essential for the efficient processing of elements in various applications, such as process scheduling, print spooling, network communication, and task management. It provides a systematic and organized approach to handling data and tasks in a sequential order, ensuring fairness and maintaining the desired order of execution.
A queue is a fundamental data structure that possesses certain properties, which define its behavior and operations. Here are the key properties of a queue:
1. FIFO (First-In-First-Out): The most important property of a queue is that it follows the FIFO principle. The element that is inserted first into the queue is the first one to be removed. This ensures that elements are processed in the order they arrived, similar to a queue or line in real-life scenarios.
2. Insertion at Rear: New elements are always inserted at the rear (end) of the queue. This maintains the order of insertion, where the element that arrived earlier remains ahead of elements that arrive later.
3. Deletion from Front: Elements are always removed from the front (head) of the queue. The element that has been in the queue the longest is the first one to be dequeued. After removal, the next element in line becomes the new front, ready to be dequeued next.
4. Limited Access: In a standard queue, access is limited to the front and rear ends. Elements in the middle of the queue cannot be directly accessed or removed unless they become the front element through dequeue operations.
5. Dynamic Size: In most implementations, a queue can dynamically grow in size to accommodate more elements. It can expand its capacity as new elements are enqueued. This allows for flexibility in managing variable amounts of data.
6. Queue Empty: A queue is considered empty when it contains no elements. In this state, both the front and rear pointers are null or point to a sentinel value. Operations like dequeue cannot be performed on an empty queue.
7. Queue Full: In some implementations, a queue may have a fixed size. When it reaches its maximum capacity, it is considered full. Additional elements cannot be enqueued until space becomes available. However, many implementations allow dynamic resizing to handle an arbitrary number of elements.
These properties ensure that a queue operates in a sequential and orderly manner, processing elements in the order they arrived. The FIFO property ensures fairness, while the insertion and deletion rules maintain the integrity of the data structure.
By understanding these properties, programmers can leverage the queue data structure to efficiently manage data and tasks in scenarios where order and fairness are essential, such as process scheduling, print spooling, and network packet routing.
Enqueue and dequeue are fundamental operations performed on a queue data structure. They are used to add elements to the rear (end) of the queue and remove elements from the front (head) of the queue, respectively. Let's explore these operations in detail:
1. Enqueue: Enqueue refers to the process of adding an element to the rear of the queue. It involves inserting the new element at the end of the queue, after all the existing elements.
The newly added element becomes the last element in the queue, ready to be processed once it reaches the front. The enqueue operation follows the FIFO (First-In-First-Out) principle, maintaining the order of insertion.
Here's how the enqueue operation works:
- If the queue is empty, the newly added element becomes both the front and rear of the queue.
- If the queue is not empty, the rear pointer is moved to the new element, and the new element is linked to the previous rear element. This ensures that the newly added element becomes the last element in the queue.
2. Dequeue: Dequeue refers to the process of removing an element from the front of the queue. The element that has been in the queue the longest is the one to be dequeued, following the FIFO principle. Once an element is dequeued, the next element in line becomes the new front, ready to be dequeued next.
Here's how the dequeue operation works:
- If the queue is empty, no element can be dequeued, as there are no elements in the queue. This is an underflow condition, and appropriate handling is required.
- If the queue is not empty, the front pointer is moved to the next element in line, effectively removing the front element from the queue. The element can then be processed or used as needed.
Both enqueue and dequeue operations are essential for managing a queue data structure and ensuring that elements are processed in the correct order. They maintain the integrity of the queue, preserving the FIFO property and allowing for sequential processing of data or tasks.
By utilizing these operations, programmers can effectively manage and manipulate queues in various applications, including process scheduling, print spooling, task management, and network packet routing.
A real-life example of a queue is a queue or line of people waiting to board a bus. Let's consider this scenario to understand how a queue works in real-life situations:
When people arrive at a bus stop and want to board a bus, they form a queue or line in a specific order. The first person to arrive at the bus stop becomes the first person in line, followed by subsequent arrivals. This queue represents the order in which people are supposed to board the bus, following the FIFO (First-In-First-Out) principle.
Here's how the real-life queue scenario parallels the concept of a queue data structure:
1. Enqueue: As people arrive at the bus stop, they join the queue by standing behind the last person in line. The newly arrived person becomes the last person in the queue, waiting for their turn to board the bus. This is similar to the enqueue operation in a queue data structure, where an element is added to the rear (end) of the queue.
2. Dequeue: When the bus arrives, the first person in the queue gets to board the bus. They move from the front of the queue to the bus, effectively leaving the queue. After that, the next person in line becomes the new front of the queue and proceeds to board the bus. This process continues until everyone in the queue has boarded the bus. This mirrors the dequeue operation in a queue data structure, where the front element is removed, and the next element becomes the new front.
3. FIFO Order: The queue of people at the bus stop ensures that everyone boards the bus in the order they arrived. The first person to join the queue is the first one to board the bus, while the last person in the queue boards the bus last. This follows the FIFO principle, maintaining the fairness and order of boarding.
This real-life example demonstrates how queues are commonly encountered and used in everyday situations. They provide an organized way to manage and process people or items in a specific order. Similar to the bus queue scenario, queues are also used in various other scenarios, such as waiting in line at a ticket counter, queuing for a movie ticket, or lining up for a service counter. The concept of queues ensures fairness and maintains the order of arrival, allowing for efficient and systematic processing.
To improve the performance of a queue, you can consider implementing certain strategies and techniques. Here are some approaches to enhance the performance of a queue data structure:
1. Choose the Right Implementation: The choice of the underlying data structure for implementing the queue can significantly impact its performance. Common implementations include arrays, linked lists, and dynamic arrays. Each has its advantages and trade-offs. For example, arrays offer constant-time access but may require resizing if the size exceeds the initial capacity.
Linked lists allow dynamic growth without resizing but may require additional memory for node allocation. Analyze the requirements of your specific use case and choose the implementation that best suits your needs.
2. Efficient Memory Management: Efficient memory management is crucial for improving queue performance. Avoid unnecessary memory allocations and deallocations. If using a linked list, consider using memory pools or pre-allocated memory blocks to reduce memory fragmentation and allocation overhead. Additionally, implement appropriate mechanisms to free memory when elements are dequeued to avoid memory leaks.
3. Dynamic Resizing: If the queue is expected to handle a large number of elements or the number of elements is unpredictable, consider using dynamic resizing techniques. Dynamic resizing allows the queue to automatically grow or shrink its capacity as needed. This helps avoid performance degradation due to frequent resizing operations. Common resizing strategies include doubling the capacity when the queue becomes full or reducing the capacity when it becomes sparsely filled.
4. Efficient Enqueue and Dequeue Operations: Optimize the enqueue and dequeue operations to minimize their time complexity. Ensure that enqueue and dequeue operations have an O(1) time complexity whenever possible. This can be achieved by maintaining proper pointers or indices to the front and rear of the queue and updating them efficiently during enqueue and dequeue operations.
5. Use Circular Queues: Circular queues, also known as ring buffers, can provide improved performance in certain scenarios. Circular queues allow efficient utilization of a fixed-size buffer by wrapping the front and rear pointers around to the beginning of the queue when they reach the end. This eliminates the need for resizing operations and reduces memory overhead.
6. Multithreading and Synchronization: If the queue is accessed concurrently by multiple threads, consider implementing thread-safe mechanisms to ensure proper synchronization. Use synchronization primitives like locks, mutexes, or atomic operations to prevent race conditions and maintain the integrity of the queue.
7. Profile and Optimize: Profile your code and identify performance bottlenecks specific to your queue implementation. Use profiling tools to measure the time taken by different operations and identify areas that need optimization. Optimize critical sections of code, such as memory allocation, pointer manipulation, or loop iterations, to improve overall performance.
Remember that the most effective optimizations depend on the specific use case and requirements of your application. It is essential to profile and measure the impact of optimizations to ensure they result in tangible performance improvements.
While queues have several advantages, they also come with certain disadvantages. Here are some of the common disadvantages of using a queue data structure:
1. Limited Access: In a standard queue, access is limited to the front and rear ends. Elements in the middle of the queue cannot be directly accessed or removed unless they become the front element through dequeue operations. This lack of random access can be a limitation in certain scenarios where direct access to arbitrary elements is required.
2. Fixed Size Limitations: If the queue is implemented with a fixed-size array or buffer, it may have limitations on the maximum number of elements it can hold. Once the queue reaches its maximum capacity, further enqueue operations may not be possible until elements are dequeued and space becomes available. This fixed size can restrict the scalability of the queue, especially in scenarios where the number of elements is unpredictable.
3. Overhead for Dynamic Resizing: If the queue needs to dynamically resize its capacity to accommodate a growing number of elements, this resizing process can introduce overhead. Resizing operations often involve memory reallocation and element copying, which can impact performance. Additionally, frequent resizing can lead to memory fragmentation, reducing memory efficiency.
4. Synchronization Challenges: In multi-threaded or concurrent environments, managing and synchronizing access to a shared queue can be challenging. Proper synchronization mechanisms need to be implemented to avoid race conditions and ensure thread safety. This adds complexity to the implementation and can introduce performance overhead due to synchronization primitives.
5. Performance for Large Queues: The performance of certain operations, such as enqueue and dequeue, can degrade as the size of the queue increases. For example, if the queue is implemented using a linked list, enqueueing at the rear requires traversing the entire list to reach the end, resulting in a linear time complexity. Similarly, dequeuing from the front may require updating pointers or indices, which can introduce overhead.
6. Memory Overhead for Linked List Implementation: If a linked list is used to implement the queue, additional memory overhead is incurred due to the need to allocate memory for nodes. Each node typically requires additional memory for storing pointers, which can result in increased memory consumption compared to an array-based implementation.
It's important to consider these disadvantages in the context of your specific use case. While queues provide valuable functionality for managing data in a sequential order, it's essential to evaluate their limitations and determine if they align with the requirements and constraints of your application.
• No, a standard queue data structure is not typically used for recursion. Recursion is a programming technique where a function calls itself to solve a problem by breaking it down into smaller subproblems. On the other hand, a queue is primarily designed for sequential processing of data in a FIFO (First-In-First-Out) order.
• While recursion involves calling the same function within itself, a queue does not have the inherent capability to call functions or execute code. It is a linear data structure that manages elements based on their order of insertion and removal.
• That said, queues can be used in combination with recursion in certain scenarios. For example, a queue can be used as a data structure to store elements in a recursive algorithm for breadth-first search (BFS) or level-order traversal of a tree or graph. In these cases, the queue is used to process nodes or elements in a specific order while the recursive function handles the logic and decision-making process.
• The queue acts as a temporary storage mechanism to hold elements to be processed or visited, ensuring that they are processed in the desired order. The recursive function uses the queue to enqueue or dequeue elements as needed and makes recursive calls to itself to traverse the data structure.
• So, while a queue itself is not used for recursion, it can be employed in conjunction with recursion to manage the order of processing elements in certain algorithms. This combination allows for efficient traversal and processing of data structures such as trees or graphs, ensuring that the desired order of exploration is maintained.






