Sorting Algorithms
Sorting is a skill that every software engineer and developer should be familiar with. Not only in order to pass coding interviews, but also to have a general
understanding of programming. The many sorting algorithms are an excellent example of how algorithm design influences programme complexity, speed, and efficiency.
First and foremost, a broad question. What exactly does a sorting algorithm accomplish? If the name sorting wasn't clear enough, a sorting algorithm's duty is to take
an unorganised list of numbers and, well, order them.
Sorting an unordered list of integers gives you a lot more control over the numbers. Sorted lists make it easier to extract the information hidden inside the numbers.
But, before I get into the specifics of each sorting algorithm, I'd like to emphasise the importance of both the foundation (particularly Big-O) and the structure.
So, without further ado, let’s dive right in.

Sorting Algorithms
⌚ What is sorting in-place?
The result of an in-place sorting algorithm is produced using constant space (modifies the given array only). It just sorts the list by changing the order of the list's components. Insertion Sort and Selection Sorts, for example, are in-place sorting algorithms since they do not require any additional space to sort the list, although a normal Merge Sort implementation is not, and neither is the implementation for counting sort.
⌚ What do you mean by stable sorting algorithms?
When two items with equal keys appear in the same order in the sorted
output as they do in the input array to be sorted, the sorting algorithm is said to be stable.
Assume A is an array, and "<" is a strict weak ordering on the items of A. Then A will be called stable if
• i < j and A[i] ≡ A[j] implies π(i) < π(j)
where π is the permutation of sorting ( sorting moves A[i] to position π(i))
Bubble Sort, Insertion Sort, Merge Sort, Count Sort, and other sorting algorithms are naturally stable.
⌚ Can any sorting algorithm be made stable?
Any unstable sorting algorithm can be tweaked to become stable. There may be specific ways to make a sorting algorithm stable, but in general, any comparison-based sorting algorithm that is not stable by nature can be modified to be stable by changing the key comparison operation so that the comparison of two keys takes position into account for objects with equal keys.
⌚ What is the difference between internal and external sortings?
External sorting is used when all of the data that has to be sorted cannot be stored in memory at the same time. For large amounts of data, external sorting is used. For external sorting, Merge Sort and its variants are commonly employed. External sorting is done with hard discs, CDs, and other external storage devices. Internal sorting is used when all of the data is kept in memory.
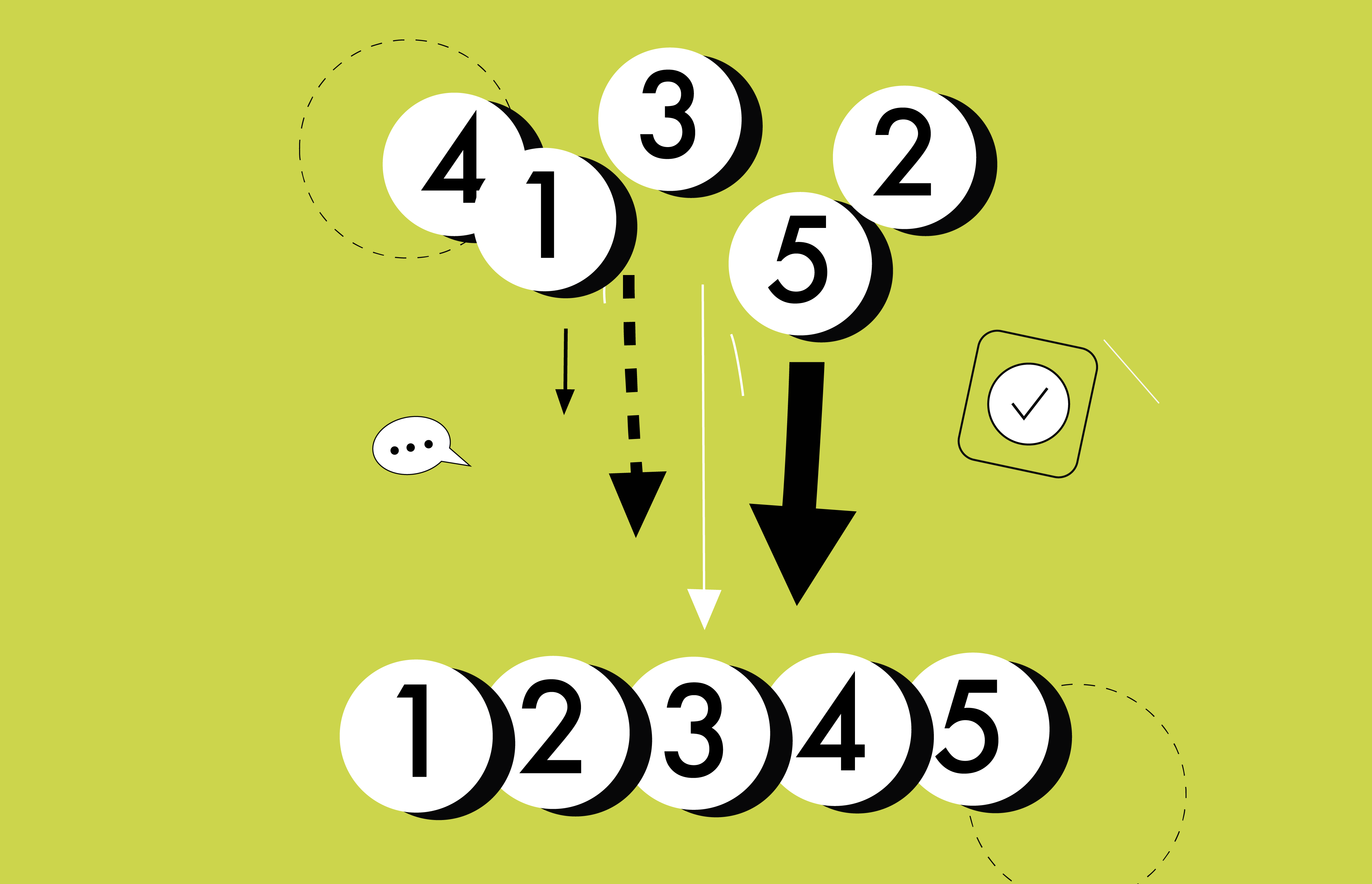
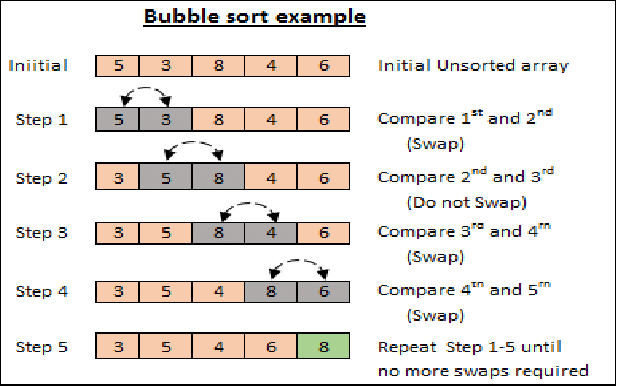
⌚ Briefly explain Bubble Sort
Bubble Sort is the most basic sorting algorithm, which works by exchanging neighbouring components in the wrong order repeatedly. Because of its average and worst
case time complexity, this approach is not suitable for huge data sets.
So, how does it function?
Bubble sort looks at each pair of neighbouring numbers as it passes over the array of integers. The lower number will be placed on the left, towards the beginning of the array,
while the larger number will be placed on the right, near the end. This process is repeated, with bubble sort looping around the array until no swaps are done, resulting in a sorted array.
Let's see in the gif that larger pieces are constructed first, and smaller elements take longer to reach the bottom.

Algorithm of Bubble Sort
bubbleSort(array) for i <- 1 to indexOfLastUnsortedElement-1 if leftElement > rightElement swap leftElement and rightElement end bubbleSort
Let's Implementation of Bubble Sort
## Python def bubbleSort(arr): n = len(arr) # Traverse through all array elements for i in range(n): # the final i parts have already been included. for j in range(0, n-i-1): #swap if the element obtained is greater than n-i-1 traverse the array from 0 to n-i-11 # than the next element if arr[j] > arr[j+1]: arr[j], arr[j+1] = arr[j+1], arr[j] # Driver code to test above arr = [23,10,1,0,9,8] bubbleSort(arr) print("Sorted array is:") for i in range(len(arr)): print("%d" % arr[i], end=" ")
Implementation in Java
class BubbleSort { void bubbleSort(int arr[]) { int n = arr.length; for (int i = 0; i < n - 1; i++) for (int j = 0; j < n - i - 1; j++) if (arr[j] > arr[j + 1]) { // swap arr[j+1] and arr[j] int temp = arr[j]; arr[j] = arr[j + 1]; arr[j + 1] = temp; } } /* Prints the array */ void printArray(int arr[]) { int n = arr.length; for (int i = 0; i < n; ++i) System.out.print(arr[i] + " "); System.out.println(); } // Driver method to test above public static void main(String args[]) { BubbleSort ob = new BubbleSort(); int arr[] = { 12,1,23,2,55,0 }; ob.bubbleSort(arr); System.out.println("Sorted array"); ob.printArray(arr); } }
Worst and Average Case Time Complexity: O(N2) When an array is reverse sorted, the worst case scenario occurs.
Best Case: When an array is already sorted, the best case scenario occurs.
Space Complexity: O(1)
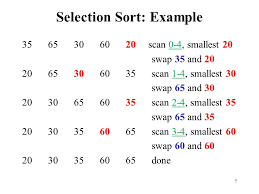
⌚ Briefly explain Selection Sort?
The selection sort algorithm sorts an array by repeatedly picking the smallest member from the unsorted segment and placing it at the beginning (in ascending order).
In a given array, the method keeps two subarrays.
• The subarray that has previously been sort
• The remaining unsorted subarray.
In each iteration of selection sort, the unsorted subarray's minimal element (in ascending order) is chosen and moved to the sorted subarray.
Algorithms:
selectionSort(array, size) repeat (size - 1) times set the first unsorted element as the minimum for each of the unsorted elements if element < currentMinimum set element as new minimum swap minimum with first unsorted position end selectionSort
Implementation in Python
import sys A = [9,1,2,3,11] # Traverse through all array elements for i in range(len(A)): # Find the smallest element in the remaining elements # unsorted array min_idx = i for j in range(i+1, len(A)): if A[min_idx] > A[j]: min_idx = j # Swap the initial element with the discovered minimum element A[i], A[min_idx] = A[min_idx], A[i] # Driver code to test above print ("Sorted array") for i in range(len(A)): print("%d" %A[i],end=" ")
Implementation in Java
// Selection Sort implementation in Java programme class SelectionSort { void sort(int arr[]) { int n = arr.length; // Move one by one. unsorted subarray border for (int i = 0; i < n-1; i++) { // In an unsorted array, find the smallest element. int min_idx = i; for (int j = i+1; j < n; j++) if (arr[j] < arr[min_idx]) min_idx = j; // Swap the found minimum element with the first // element int temp = arr[min_idx]; arr[min_idx] = arr[i]; arr[i] = temp; } } // Prints the array void printArray(int arr[]) { int n = arr.length; for (int i=0; i<n; ++i) System.out.print(arr[i]+" "); System.out.println(); } // Driver code to test above public static void main(String args[]) { SelectionSort ob = new SelectionSort(); int arr[] = {6,2,1,3,99,0}; ob.sort(arr); System.out.println("Sorted array"); ob.printArray(arr); } }
Selection Sort has an O(N2) time complexity since it has two nested loops:
One loop to select each Array element one by one = O(N)
Another loop to compare that element to each other element in the array = O(N)
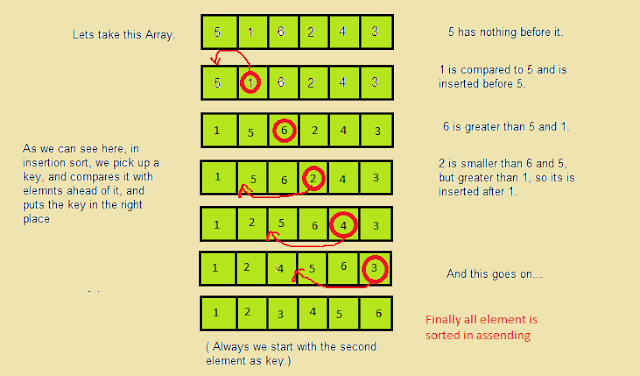
⌚ Briefly explain Insertion Sort?
Insertion sort is a simple sorting algorithm that operates in the same way that you arrange cards in your hands. The array is divided into two sections: sorted and unsorted.
The values from the unsorted component are selected and placed in the sorted part in the proper order.
Insertion Sort Characteristics
This algorithm is one of the most straightforward to implement.
Insertion sort is most effective for little data values.
Insertion sort is adaptive in nature, which means it works well with partially sorted data sets.
Algorithm:
insertionSort(array) mark first element as sorted for each unsorted element X 'extract' the element X for j <- lastSortedIndex down to 0 if current element j > X shift sorted element to the right by one break loop and insert X here end insertionSort
Implementation in Python
# Insertion sort in Python def insertionSort(array): for step in range(1, len(array)): key = array[step] j = step - 1 # Compare the key to each element to the left of it until you find one that is smaller. # For descending order, change key<array[j] to key>array[j]. while j >= 0 and key < array[j]: array[j + 1] = array[j] j = j - 1 # Place the key after the element that is somewhat smaller than it. array[j + 1] = key data = [2,1,4,32,0] insertionSort(data) print('Sorted Array in Ascending Order:') print(data)
Implementation in Java
// Insertion sort in Java import java.util.Arrays; class InsertionSort { void insertionSort(int array[]) { int size = array.length; for (int step = 1; step < size; step++) { int key = array[step]; int j = step - 1; // Compare key with each element to the left of the key until an element smaller than it appears. // it is found. // For descending order, change key<array[j] to key>array[j]. while (j >= 0 && key < array[j]) { array[j + 1] = array[j]; --j; } // Place key at after the element just smaller than it. array[j + 1] = key; } } // Driver code public static void main(String args[]) { int[] data = { 2,1,4,2,0 }; InsertionSort is = new InsertionSort(); is.insertionSort(data); System.out.println("Sorted Array in Ascending Order: "); System.out.println(Arrays.toString(data)); } }
Best Case Complexity: It occurs when there is no need to sort the array because it is already sorted. Insertion sort's best-case time complexity is O(n).
Average Case: It happens when the array elements are in a jumbled order that is neither ascending nor descending properly. Insertion sort has an average time complexity of O(n2).
Worst Case: When the array elements must be sorted in reverse order, this occurs. Assume you need to sort the array elements in ascending order, but the elements themselves are sorted in descending order. Insertion sort's worst-case time complexity is O(n2).
Space Complexity: O(1)
⌚ Briefly explain Merge Sort?
Merge sort is one of the most efficient sorting algorithms. It operates on the divide-and-conquer principle. Merge sort continuously cuts down a list into numerous sublists until each sublist contains only one entry, then merges those sublists into a sorted list.
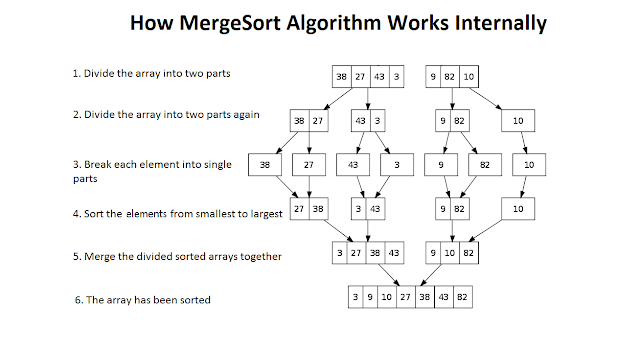
The MergeSort function divides the array in half periodically until we reach a point when we try to MergeSort on a subarray of size 1, i.e. p == r. After that, the merge function takes over, merging the sorted arrays into larger arrays until the entire array has been merged.
Merge_Sort(Arr, low, high):
if low > high
return
mid = (low + high)/2
Merge_Sort(Arr, low, mid)
Merge_Sort(Arr, mid + 1, high)
merge(Arr, low, mid, high)
Applications of Merge Sort
Merge Sort can be used to sort linked lists in O(nLogn) time. The scenario for linked lists is unique, owing to the differences in memory allocation between arrays and linked lists. Unlike arrays, linked list nodes in memory may not be adjacent. Unlike an array, we can insert items in the middle of a linked list in O(1) extra space and O(1) time. As a result, the merge sort operation can be performed without requiring any additional linked list space.
Implementation in Python
# Merge two sorted sublists `A[low … mid]` and `A[mid+1 … high]` def merge(A, aux, low, mid, high): k = low i = low j = mid + 1 # While both the left and right runs have elements while i <= mid and j <= high: if A[i] <= A[j]: aux[k] = A[i] k = k + 1 i = i + 1 else: aux[k] = A[j] k = k + 1 j = j + 1 # Copy remaining elements while i <= mid: aux[k] = A[i] k = k + 1 i = i + 1 # No need to copy the second half (since the remaining items # are already in their correct position in the auxiliary array) # copy back to the original list to reflect sorted order for i in range(low, high + 1): A[i] = aux[i] # Sort list `A[low…high]` using auxiliary list aux def mergesort(A, aux, low, high): # Base case if high == low: # if run size == 1 return # find midpoint mid = (low + ((high - low) >> 1)) # recursively split runs into two halves until run size == 1, # then merge them and return up the call chain mergesort(A, aux, low, mid) # split/merge left half mergesort(A, aux, mid + 1, high) # split/merge right half merge(A, aux, low, mid, high) # merge the two half runs # Function to check if `A` is sorted in ascending order or not def isSorted(A): prev = A[0] for i in range(1, len(A)): if prev > A[i]: print("MergeSort Fails!!") return False prev = A[i] return True # Implementation of merge sort algorithm in Python if __name__ == '__main__': A = [9,6,5,4,3,2,22,1,0] aux = A.copy() # sort list `A` using auxiliary list `aux` mergesort(A, aux, 0, len(A) - 1) if isSorted(A): print(A)
Implementation in C++
// Merge sort in C++ #include <iostream> using namespace std; // Merge two subarrays L and M into arr void merge(int arr[], int p, int q, int r) { // Create L ← A[p..q] and M ← A[q+1..r] int n1 = q - p + 1; int n2 = r - q; int L[n1], M[n2]; for (int i = 0; i < n1; i++) L[i] = arr[p + i]; for (int j = 0; j < n2; j++) M[j] = arr[q + 1 + j]; // Maintain current index of sub-arrays and main array int i, j, k; i = 0; j = 0; k = p; // Until we reach either end of either L or M, pick larger among // elements L and M and place them in the correct position at A[p..r] while (i < n1 && j < n2) { if (L[i] <= M[j]) { arr[k] = L[i]; i++; } else { arr[k] = M[j]; j++; } k++; } // When we run out of elements in either L or M, // pick up the remaining elements and put in A[p..r] while (i < n1) { arr[k] = L[i]; i++; k++; } while (j < n2) { arr[k] = M[j]; j++; k++; } } // Divide the array into two subarrays, sort them and merge them void mergeSort(int arr[], int l, int r) { if (l < r) { // m is the point where the array is divided into two subarrays int m = l + (r - l) / 2; mergeSort(arr, l, m); mergeSort(arr, m + 1, r); // Merge the sorted subarrays merge(arr, l, m, r); } } // Print the array void printArray(int arr[], int size) { for (int i = 0; i < size; i++) cout << arr[i] << " "; cout << endl; } // Driver program int main() { int arr[] = {0,6,3,2,1,8,99,7}; int size = sizeof(arr) / sizeof(arr[0]); mergeSort(arr, 0, size - 1); cout << "Sorted array: \n"; printArray(arr, size); return 0; }
Merge Sort is a fast algorithm with an O(n*log n) time complexity. It's also a stable sort, meaning the "equal" entries in the sorted list are in the same order.
As we taught in Binary Search, whenever we divide a number in half at each step, we can express it with a logarithmic function, log n, and the number of steps may be represented with log n + 1. (at most)
In addition, we use a one-step method to find the middle of any subarray, i.e. (1). A running time of O(n) will be required to merge the subarrays created by dividing the initial array of n elements. As a result, the overall time for the mergeSort function will be n(log n + 1), giving us an O(n*log n) time complexity.
Space Complexity: O(n)
⌚ Briefly explain quick sort?
Quick Sort is a regularly used sorting algorithm in computer science. Quick Sort employs a divide-and-conquer strategy. It makes two empty arrays to hold elements less than the pivot value and elements more than the pivot value, then sorts the sub arrays recursively. The algorithm consists of two basic operations: swapping items in place and splitting a segment of the array.
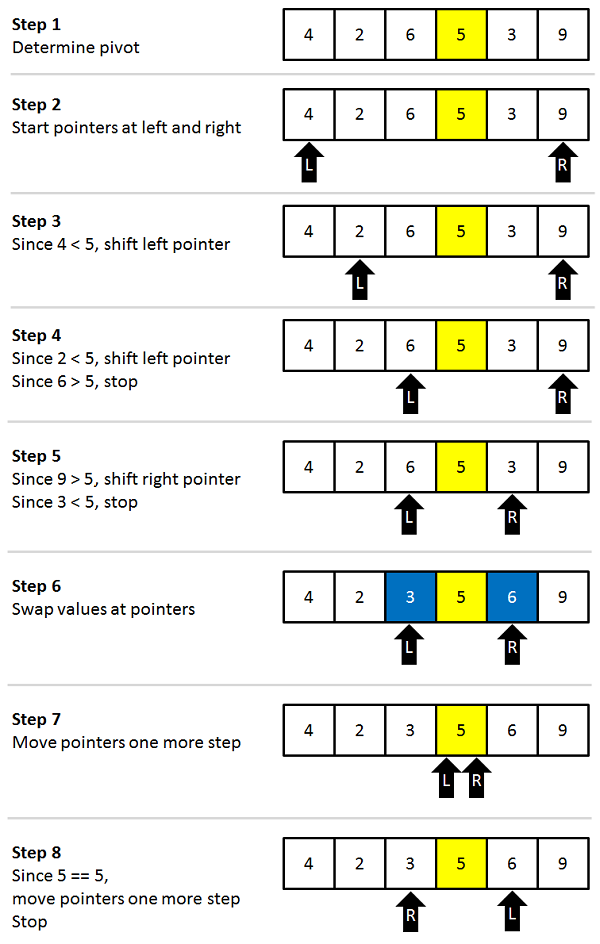
Quick Sort Algorithm: Steps
⮞ In the array, look for a "pivot" entry. For a single round, this object serves as the comparison point.
⮞ Begin with the first item in the array (the left pointer).
⮞ Begin a pointer (the right pointer) at the array's last item.
⮞ Move the left pointer to the right while the value at the left pointer in the array is smaller than the pivot value (add 1). Continue until the pivot value is larger
than or equal to the value at the left pointer.
⮞ Move the right pointer to the left while the value at the right pointer in the array is greater than the pivot value (subtract 1). Continue until the
pivot value is less than or equal to the right-hand pointer value.
⮞ Swap the values at these points in the array if the left pointer is less than or equal to the right pointer.
⮞ Move the left pointer one space to the right and the right pointer one space to the left.
⮞ Return to step 1 if the left and right pointers do not meet.
Algorithm:
/* low --> Starting index, high --> Ending index */ quick_sort(arr[], low, high) { if (low < high) { /* pi is the index of partitioning, arr[pivot] is now at right place */ pi = partition(arr, low, high); quick_sort(arr, low, pi - 1); // Before pi quick_sort(arr, pi + 1, high); // After pi } } partition (arr[], low, high) { // pivot element has to placed at right pos pivot = arr[high]; i = (low - 1) // Index of smaller element and indicates the // So far, the correct pivot position has been discovered for (j = low; j <= high- 1; j++) { // If current element is smaller than the pivot if (arr[j] < pivot) { i++; // increment index of smaller element swap arr[i] and arr[j] } } swap arr[i + 1] and arr[high]) return (i + 1) }
Implementation in Python
# Python program for Quicksort # This function takes last element as pivot, places # the pivot element at its correct position in sorted # array, and places all smaller (smaller than pivot) # to left of pivot and all greater elements to right # of pivot def partition(arr,low,high): i = ( low-1 ) # index of smaller element pivot = arr[high] # pivot for j in range(low , high): # If current element is smaller than or # equal to pivot if arr[j] <= pivot: # increment index of smaller element i = i+1 arr[i],arr[j] = arr[j],arr[i] arr[i+1],arr[high] = arr[high],arr[i+1] return ( i+1 ) # The main function that implements QuickSort # arr[] --> Array to be sorted, # low --> Starting index, # high --> Ending index # Function to do Quick sort def quickSort(arr,low,high): if low < high: # arr[p] is now partitioning index, pi is partitioning index. # at right place pi = partition(arr,low,high) # Separately sort elements before # partition and after partition quickSort(arr, low, pi-1) quickSort(arr, pi+1, high) # Driver code to test above arr = [11,1,1,2,1,3,4,5] n = len(arr) quickSort(arr,0,n-1) print ("Sorted array is:") for i in range(n): print ("%d" %arr[i]),
Implementation in C++
Quicksort example program in c++: #include<iostream> #include<cstdlib> using namespace std; // Swapping two values. void swap(int *a, int *b) { int temp; temp = *a; *a = *b; *b = temp; } // Partitioning the array based on high values as the pivot value. int Partition(int a[], int low, int high) { int pivot, index, i; index = low; pivot = high; // Getting index of the pivot. for(i=low; i < high; i++) { if(a[i] < a[pivot]) { swap(&a[i], &a[index]); index++; } } // Swapping value between the high and the obtained index. swap(&a[pivot], &a[index]); return index; } // Random selection of pivot. int RandomPivotPartition(int a[], int low, int high) { int pvt, n, temp; n = rand(); // In the provided subpart of the array, randomise the pivot value. pvt = low + n%(high-low+1); // Switching the pivot value from high to low, such that the pivot value is used as a pivot during partitioning. swap(&a[high], &a[pvt]); return Partition(a, low, high); } int QuickSort(int a[], int low, int high) { int pindex; if(low < high) { // Partitioning array using randomized pivot. pindex = RandomPivotPartition(a, low, high); // Recursively implementing QuickSort. QuickSort(a, low, pindex-1); QuickSort(a, pindex+1, high); } return 0; } int main() { int n, i; cout<<"\nEnter the number of data elements to be sorted: "; cin>>n; int arr[n]; for(i = 0; i < n; i++) { cout<<"Enter element "<<i+1<<": "; cin>>arr[i]; } QuickSort(arr, 0, n-1); // Printing the sorted data. cout<<"\nSorted Data "; for (i = 0; i < n; i++) cout<<"->"<<arr[i]; return 0; }
Worst Case Complexity: O(n2) It happens when the pivot element chosen is either the largest or smallest. As a result of this condition, the pivot element ends up at the very end of the sorted array. One sub-array is always empty, whereas the other has n - 1 elements. As a result, quicksort is only applied to this sub-array. For scattered pivots, however, the quicksort method performs better.
Best Case Complexity: It happens when the pivot element is always in the middle or close to the middle.
Space Complexity: O(n) and O(logn) for average case.
⌚ Explain heap sort?
Heap is a tree-based data structure in which all of the tree nodes are arranged in a precise sequence, allowing the tree to satisfy the heap properties (that is, there is a specific parent-child relationship that is followed throughout the tree).
The heap's root element should be at index 0 in the array.
At index (i-1)/2 is the parent node
At index (2*i)+1 is the left child node
At index (2*i)+2 is the right child node
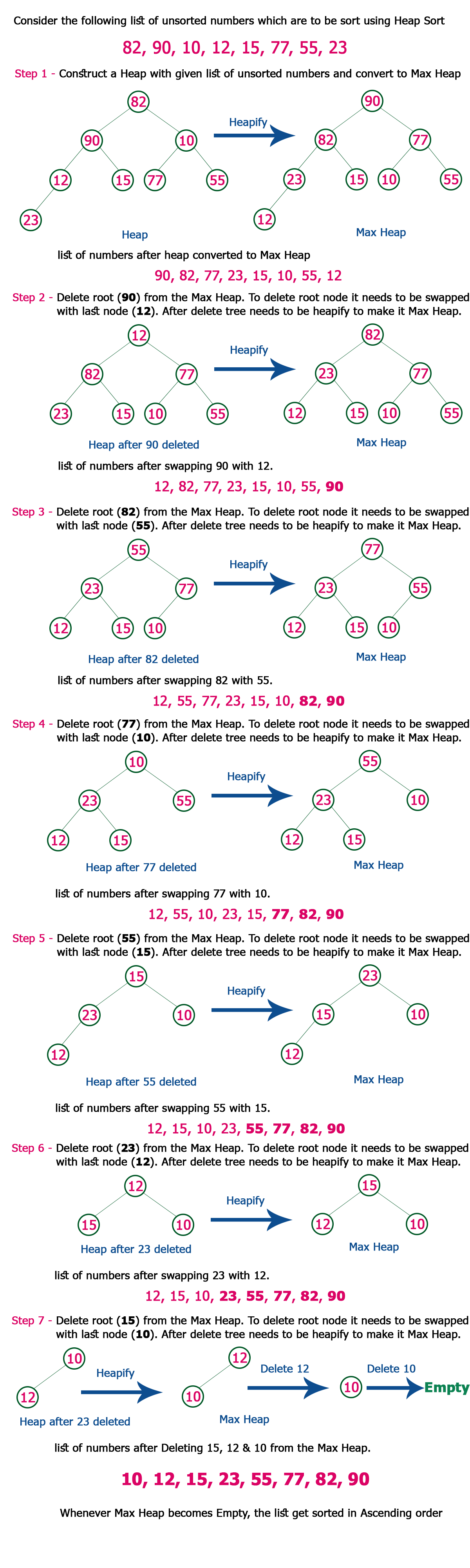
Heap sort is a comparison-based sorting algorithm that produces a heap from the input array and then sorts the array using the attributes of the heap. Please keep in mind that because the heap is a tree-based data structure, understanding the heap sort method requires knowledge of arrays, trees, binary trees, and heaps
Heapify Operation:
The process of converting a binary tree into a Heap data structure is known as 'Heapify'. A binary tree is a data structure with a maximum of two child nodes. If the children nodes of
a node have been 'heapified,' then only the 'heapify' process can be used on that node. A heap should always be a binary tree in its entirety.
Starting with a complete binary tree, we can convert it to a Max-Heap by calling the 'heapify' function on all of the heap's non-leaf items. Recursion is used by 'heapify.'
heapify(array) Root = array[0] Largest = largest( array[0] , array [2 * 0 + 1]. array[2 * 0 + 2]) if(Root != Largest) Swap_it(Root, Largest)
Heap Sort Function:
By swapping the root element with the array's last element, the heap array's length is reduced by one. It's the same as swapping the root with the bottommost and rightmost leaf and then deleting the leaf in heap representation.
After each deletion, restoring heap properties (reheapification), where we only need to use the heapify method on the root node because the subtree heaps will still have their heap properties intact at the start of the operation.
Repeat the root removal, storage in the position of the heap's greatest index value, and heap length decrement operation until all elements in the array are sorted.
This method will sort the array in ascending order on a max heap. It will sort in descending order on a small heap.
Implementation in Python
# Heap Sort in python def heapify(arr, n, i): # Find largest among root and children largest = i l = 2 * i + 1 r = 2 * i + 2 if l < n and arr[i] < arr[l]: largest = l if r < n and arr[largest] < arr[r]: largest = r # If the root isn't the biggest, replace it with the biggest and keep heapifying if largest != i: arr[i], arr[largest] = arr[largest], arr[i] heapify(arr, n, largest) def heapSort(arr): n = len(arr) # Build max heap for i in range(n//2, -1, -1): heapify(arr, n, i) for i in range(n-1, 0, -1): # Swap arr[i], arr[0] = arr[0], arr[i] # Heapify root element heapify(arr, i, 0) arr = [1,10,3,22,9,0] heapSort(arr) n = len(arr) print("Sorted array is") for i in range(n): print("%d " % arr[i], end='')
Implementation in C++
// Heap Sort in C++ #include <iostream> using namespace std; void heapify(int arr[], int n, int i) { // Find largest among root, left child and right child int largest = i; int left = 2 * i + 1; int right = 2 * i + 2; if (left < n && arr[left] > arr[largest]) largest = left; if (right < n && arr[right] > arr[largest]) largest = right; // If the root is not the largest, swap it and keep heapifying if (largest != i) { swap(arr[i], arr[largest]); heapify(arr, n, largest); } } // main function to do heap sort void heapSort(int arr[], int n) { // Build max heap for (int i = n / 2 - 1; i >= 0; i--) heapify(arr, n, i); // Heap sort for (int i = n - 1; i >= 0; i--) { swap(arr[0], arr[i]); // Heapify root element to get highest element at root again heapify(arr, i, 0); } } // Print an array void printArray(int arr[], int n) { for (int i = 0; i < n; ++i) cout << arr[i] << " "; cout << "\n"; } // Driver code int main() { int arr[] = {1,12,11,0,222,121}; int n = sizeof(arr) / sizeof(arr[0]); heapSort(arr, n); cout << "Sorted array is \n"; printArray(arr, n); }
Heapify has an O time complexity (Logn). The overall time complexity of Heap Sort is O(nlogn), whereas the time complexity of createAndBuildHeap() is O(n)
⌚ Explain Counting Sort?
Counting sort is a sorting algorithm that organises elements in an array or list by counting the number of times each unique element appears. The counting algorithm is essentially a hashing technique that counts the number of objects with distinct key values inside a certain range. Finally, we'll generate the output sequence by performing some arithmetic calculations to place each object based on its key values. Counting sort counts the number of times an element appears in O using the partial hashing technique (1). Working with counting sort has the advantage of working with negative items as well. Another sorting algorithm is used as a subroutine. The counting sort is not a comparison-based sorting algorithm with an O(n) time complexity and a space proportional to the number of elements. As a result, counting sort efficiency is highest when the range of elements is not more than the number of elements to be sorted.
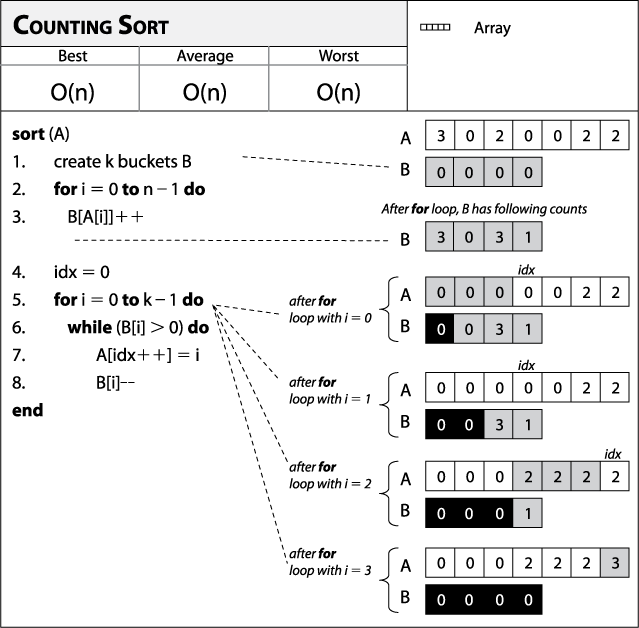
Algorithm of Counting
1. Counting Sort(array, ele) // ele is the array's element count.
2. max = finding the array's biggest element
3. then create a count array of length max + 1 and fill it with all 0s.
4. Iterate from 0 to ele
5. discover the total number of occurrences of each element and save the count in the count array at the index.
6. Iterate from 0 to max
7. To get the cumulative sum, add the current(i) and previous(i-1) counts, which you can save in the count array.
8. For j = ele down to 1
9. Decrement the count of each element copied by one before copying it back into the input array.
Implementation in Python
# Counting sort in Python def countingSort(array): size = len(array) output = [0] * size # Initialize count array count = [0] * 10 # The count of each element is stored in the count array for i in range(0, size): count[array[i]] += 1 # Store the cummulative count for i in range(1, 10): count[i] += count[i - 1] # Find the index of each element of the original array in count array # place the elements in output array i = size - 1 while i >= 0: output[count[array[i]] - 1] = array[i] count[array[i]] -= 1 i -= 1 # Copy the sorted elements into original array for i in range(0, size): array[i] = output[i] data = [1,3,2,4,6,7] countingSort(data) print("Sorted Array in Ascending Order: ") print(data)
Implementation in C++
// Counting sort in C++ #include <iostream> using namespace std; void countSort(int array[], int size) { // The size of count must be at least the (max+1) but // we cannot assign declare it as int count(max+1) in C++ as // it does not support dynamic memory allocation. // as a result, its size is specified statically. int output[10]; int count[10]; int max = array[0]; // Find the array's greatest element. for (int i = 1; i < size; i++) { if (array[i] > max) max = array[i]; } // Create a count array with all zeros. for (int i = 0; i <= max; ++i) { count[i] = 0; } // Store the count of each element for (int i = 0; i < size; i++) { count[array[i]]++; } // Store the cummulative count of each array for (int i = 1; i <= max; i++) { count[i] += count[i - 1]; } // Find the index of each element of the original array in count array, and // place the elements in output array for (int i = size - 1; i >= 0; i--) { output[count[array[i]] - 1] = array[i]; count[array[i]]--; } // Copy the sorted elements into original array for (int i = 0; i < size; i++) { array[i] = output[i]; } } // Function to print an array void printArray(int array[], int size) { for (int i = 0; i < size; i++) cout << array[i] << " "; cout << endl; } // Driver code int main() { int array[] = {4,7,9,3,2,6}; int n = sizeof(array) / sizeof(array[0]); countSort(array, n); printArray(array, n); }
The counting sort takes O(n+k) time and takes up O(n+k) space, where nn is the number of items to sort and k is the number of potential values. We go over the input items twice, once to populate the counts and once to fill in the output array. Both iterations take O(n) time to complete. We also fill in nextIndex by iterating through counts once, which takes O(k) time. Three extra arrays are allocated by the algorithm: one for counts, one for nextIndex, and one for output. The first two are in O(k) space, whereas the third is in O(n) space.
🚀Conclusion
This page has finally come to a conclusion. You should be able to design your own programmes with the material on this page and little study, and small projects are actually encouraged for improving your programming skills. A single course cannot possibly cover everything you need to know to be a good programmer. Whether you're a seasoned professional developer or a complete novice, programming is a never-ending learning process.






