1. Course Curriculum

Name: Data structures and Algorithms Course
Brand: LogicMojo
SKU: .
Rating: 4.9 (18654 reviews)

Master DSA and System Design with a curriculum crafted by senior engineers from top tech companies. We provide the practical skills and insider knowledge needed to excel in demanding SDE roles.

Learn from Experts

Live Interactive Sessions

Learn directly from senior engineers who bring years of real-world experience from top product companies.

Competitive Coding Tests

Sharpen your skills with assignments and tests curated by our expert instructors to mirror real interview questions.

Collaborative Learning

Grow with a community of motivated peers. Solve problems together and build a strong professional network you can trust.

Gain Real-World Experience

Practical Experience through Projects

Build a portfolio with hands-on projects that demonstrate your ability to apply concepts to solve real-world problems, showcasing your experience.

Authoritative Job Assistance

Get interview-ready with resume reviews and mock interviews conducted by hiring managers, giving you an authoritative edge.

Your Trustworthy Support System

1:1 Doubt Clearing Sessions

Never get stuck. Our dedicated TAs are available for unlimited 1:1 sessions, building trust and ensuring you understand every concept.

Lifetime Access & Updates

Your learning journey doesn't end. Get lifetime access to all course materials, including future updates. A promise you can trust.

Transparent & Flexible Pay

Invest in your future with clear, upfront pricing and easy EMI options. No hidden fees. A trustworthy commitment to your success.

Curriculum Deep-Dive

Explore the depth of our expert-designed curriculum.

Arrays & Hashing: Store and retrieve items efficiently using indexed collections and key-value pairs.
LinkedList: Manage dynamic data with nodes that link to one another in a sequence.
Stack & Queues: Handle data with Last-In, First-Out (LIFO) and First-In, First-Out (FIFO) principles.
Trees & Tries Organize data hierarchically for optimized searching and storing complex relationships.
Heaps / Priority Queues: Quickly access the most important items in a collection based on priority.
Graph & Matrix: Model and solve problems involving complex networks and multi-dimensional data.

Two Pointers: Traverse data structures from both ends to find pairs or subarrays efficiently.
Sliding Window: Analyze subsets of data by moving a fixed-size window across a larger collection.
Backtracking: Explore all possible solutions by incrementally building and undoing choices.
BFS & DFS: Systematically traverse or search through graphs and trees, layer by layer or branch by branch.
Dynamic Programming: Solve complex problems by breaking them down into simpler, overlapping subproblems.
Greddy Algorithms: Make the locally optimal choice at each step with the hope of finding a global optimum.

2. About Online DSA Course

This is more than a course—it's your career transformation blueprint. Designed by architects of scalable systems and hiring managers, it provides the precise, in-demand skills and validated strategies you need to break into the industry's most coveted roles.

See Your Transformation

From College to a Top Company

You have the theoretical knowledge but lack the practical skills to crack tough interviews.

Key Outcomes:

Expert Problem-Solver: Confidently solve LeetCode Hard problems.
Project Portfolio: Build 2-3 impressive, real-world projects.
Career Launch: Land an SDE-1 role at a top product company.

From Service to Product-Based

You're stuck in a service-based role and want to transition to a high-growth product company.

Key Outcomes:

System Design Mastery: Design scalable, real-world systems with confidence.
Interview Ace: Crack MAANG-level interviews with mock sessions from hiring managers.
Significant Salary Hike: Achieve a 150%+ average salary increase, based on our alumni data.

From Manager to Tech Visionary

You lead teams but want to deepen your technical authority to drive innovation.

Key Outcomes:

Architectural Authority: Make high-level design decisions with confidence.
Mentor with Expertise: Effectively guide and mentor your team on technical challenges.
Drive Innovation: Stay ahead of tech trends and lead your team to build better products.

Frequently Asked Questions

Our expert-designed curriculum is focuses on the high-impact skills demanded by top companies. You will master:

1. Core Data Structures: Arrays, Linked Lists, Stacks, Queues, Trees, Tries, Heaps, and Graphs.
2. Advanced Algorithms: Dynamic Programming, Greedy Algorithms, Backtracking, and complex Graph algorithms like Dijkstra's and Floyd-Warshall.
3. System Design: Scalability, Caching, Load Balancing, Database Sharding, and designing systems like TinyURL or a chat application from scratch.
4. Problem-Solving: A systematic approach to deconstruct any complex problem, a skill honed through hundreds of practice problems.

We believe in building talent from the ground up, which is why our course is designed to be accessible. All you need is:

1. A basic understanding of any one programming language (like C++, Java, or Python).
2. A strong desire to learn and a commitment to consistent practice.

We provide a trustworthy environment where we start with the absolute basics and build up to advanced concepts, ensuring no one is left behind.

Our program is your direct pathway to high-paying roles in the tech industry. Our alumni have an authoritative track record of success, landing roles such as:

1. Software Development Engineer (SDE) I & II at product-based companies.
2. Backend Developer, Full-Stack Developer.
3. Specialized roles in companies like Google, Microsoft, Amazon, and other top-tier startups.

Based on our alumni data, graduates see an average salary hike of 120-150%, a testament to the value and experience gained in our course.

Your DSA & System Design Journey

First 4 Months: Data Structures & Algorithms

Master the fundamentals of algorithmic thinking and problem solving

Time Complexity

Learn fundamentals of programming and understand time complexity.

Big O Notation Space Complexity Algorithm Analysis

Topic Duration → 2 weeks

Array, String and Linked List

Master array, string, sorting and linked list and implement real time project on Git and GitHub.

Array Operations String Manipulation Linked Lists Sorting

Topic Duration → 3 weeks

Stack and Queue

Learn fundamentals of programming of stack and queue and its usage.

Stack Implementation Queue Applications Problem Solving

Topic Duration → 3 weeks

Hashing & Heap Sort

Learn fundamentals of programming the hashing/heap sort in very simpler way.

Hash Functions Collision Resolution Heap Operations

Topic Duration → 4 weeks

OOD Concepts

Learn fundamental OOD concepts and its usage in programming.

Encapsulation Inheritance Polymorphism Object Oriented Design

Topic Duration → 4 weeks

Competitive Programming

String based and mathematical competitive programming practise, Hackerank, Hackerearch Practise in Live classes

String Manipulation Mathematical Problems HackerRank HackerEarth

Topic Duration → Ongoing

Binary Tree, N-ary Tree, Segment Tree etc

Learn fundamentals of binary tree and N-ary tree and use it project/assignments.

Binary Tree N-ary Tree Segment Tree Tree Traversal

Topic Duration → 4 weeks

Greedy Algorithm

Learn all about Greedy Algorithms and its use cases.

Greedy Algorithms Algorithm Design

Topic Duration → 3 weeks

Backtracking & Recursion

Learn fundamentals of Backtracking and Recursion.

Recursion Backtracking Algorithm Design

Topic Duration → 3 weeks

Graph Theory

Learn fundamentals of Graph Theory and its applications.

Graph Traversal Shortest Paths Minimum Spanning Trees Network Flow

Topic Duration → 4 weeks

Dynamic Programming

Learn Dynamic Programming and its key concepts.

Memoization Tabulation Optimal Substructure Overlapping Subproblems

Topic Duration → 4 weeks

Advanced Data Structures

Complete Advanced data structures like Trie, Suffix Tree, Suffix Array, ternary search trees etc.

Trie Suffix Tree Suffix Array Ternary Search Trees

Topic Duration → 4 weeks

4 months

Next 3 Months: System Design

Learn how to design scalable and efficient systems

System Design Basics

Approach of system design problem, discuss requirement, API, data model, system components, system interface & design.

API Design Data Modeling System Components System Interface Consistency Availability Latency

Topic Duration → 3 weeks

Distributed System Basics

Distributed Database, SQL, Load Balancer, Distributed Cache, CDN, Cache Eviction Policies, Push & Pull Mechanism, CAP Theorem etc.

Distributed Databases SQL Load Balancing Caching CDN CAP Theorem

Topic Duration → 3 weeks

Cloud Architecture Deployment

EC2 Instance configuration, Docker Container Deployment, cloud-native development, Pods, Running Web App in docker.

EC2 Docker Cloud-Native Pods

Topic Duration → 3 weeks

Design Patterns

SOLID Design pattern, Singleton design pattern, factory & abstract factory design pattern, Builder design pattern, observer design pattern etc.

SOLID Creational Patterns Behavioral Patterns Singleton

Topic Duration → 2 weeks

SQL & NoSQL

SQL Relational/Non- Relational Database, MYSQL and NoSQL – key/value Model, Cassandra, MongoDB, Redis etc. Document Databases, Graph Databases.

Relational DBs NoSQL Systems Data Modeling MySQL Cassandra MongoDB Redis

Topic Duration → 2 weeks

Kubernetes, Docker Deployment

Scalability (Latency, Throughput, vertical scaling, Horizontal scaling), AWS, Kubernetes Architecture & ecosystem, Long-Polling, web-sockets etc.

Scalability Kubernetes Docker AWS

Topic Duration → 2 weeks

Distributed Cache, Database Sharding

Caching, Cache Eviction Policies, Consistent Hashing, Zookeeper, Pooling & Streaming Concepts, Publish/Subscribe Pattern, Map Reduced.

Caching Database Sharding Consistent Hashing Zookeeper

Topic Duration → 3 weeks

Microservice Architectures Details

Monolithic vs microservices, micro-service Architectures, fault tolerance scalable system, Service Discovery, Distributed Tracing and Monitoring etc

Microservices Monolithic Service Discovery Distributed Tracing

Topic Duration → 2 weeks

Big Data, Hadoop Kafka, Zookeeper

Complete Understanding of Big Data Tech, High Level and Low Level Internal System Design, Message Queue, Kafka, API gateway, Big Data, Service Mesh

Big Data Hadoop Kafka Zookeeper Message Queue

Topic Duration → 3 weeks

Scalable System Design Problems Discussion

Design Problems of Real world system, Tiny URL, paste bin, Uber design, Facebook design, G-Map, Swiggy location based system, Mail server(Gmail) , WhatsApp etc

System Design Scalability Real-world Systems

Topic Duration → Ongoing

High level Design(HLD) + LLD(Low Level Design)

Understanding all scalable distributed system design, HLD and LLD detail design discussion, Detail Architectural Design flow, Distributed Components etc

High Level Design Low Level Design Distributed Systems

Topic Duration → Ongoing

System Design Interview Questions

System Design Interview question discussion with various examples. How design works, how to explain the design & cover bottle neck design issues

System Design Interview Preparation Problem Solving

Topic Duration → Ongoing

3 months

Advanced Scalable System Design course

(Duration - Next 3 months)

This system design course is designed by senior engineers from product-based companies to help you crack High-Level Design (HLD) and Low-Level Design (LLD) interviews at top tech companies.

Download brochure

Approach to solve any system design problem
Requirements gathering, API design, data modeling
System components, system interface & design trade-offs
Consistency, Availability, Partition Tolerance (CAP Theorem)
Latency vs Throughput, Scalability principles

Distributed database fundamentals
SQL vs NoSQL design choices
Sharding, replication, partitioning strategies
ACID vs BASE, eventual consistency

Load Balancer types & algorithms (Round Robin, Least Connections, IP Hash)
Distributed Cache (Redis, Memcached) & cache eviction policies (LRU, LFU)
CDN strategies, push vs pull mechanism
Rate limiting & throttling techniques

Advanced DSA & Problem Solving course

(Duration - First 4 months)

This course is curated by leading faculties and industry leaders to provide practical learning experience with live interactive classes and projects.

Download brochure

• Order complexity analysis
• What is Big 0 Notation, how to use it with various examples.

What is space & time complexity, examples to find out space time complexity

• Understanding Average, Best and Worst case of various programs.
• Analysis of Loops, Time Complexity of Loop with Powers

More complex examples which involves multiples exponential loops .

What is recursion, how to analyse recursion in call stacks .

• Understanding code flow of recursive call with examples

• Difference between recursive and iterative approaches
• Find space complexity of recursive calls.

• More Complex examples involve recursion calls,

Understanding the Array computations with examples .
Implementation of Array problems

Why do we need arrays ?
Array Advantages And Limitation over other data structures

Matrix related Problem(2-D array)
Minimum Window Substring
Two pointers approach etc

Linting, formatting, understanding Python code,
Array problems involves searching
Array sorting efficient algorithms

Discussion of Top product companies interview questions based on Array

Most asked interview question are based on strings.
How to efficiently solve strings problems

Tricks of solving the strings problems techniques
Two pointers tricks, window based problems etc

Discussion of Top product companies interview questions based on String

Linked List creation implementation
Adding,deleting and finding specific nodes

Implementation of Doubly linked list
Implementation of Circular linked list
Problems based on DLL, Circular LinkedList.

Merge two sorted linked lists, merge sort of a linked list
Reversing a linked list, k group Linked List etc

Discussion of top product companies interview questions based on DLL, LinkedList

Introduction to Trees.
Making a tree node class
Tree traversals
Destructor for tree node class

Balanced Trees, How to maintain Tree Balance
Self-balancing tree

In Order, Pre and Post-Order using recursion
Problems based on Binary Tree traversal
What Is a Binary Search Tree Used For?
Left view, right view, bottom view of binary tree etc

Discussion of Top product companies interview questions based on Binary tree

Introduction to Binary Search Trees
Searching a node in BST
Inserting and Deleting nodes in BST
Types of balanced BSTs

Discussion of Top product companies interview questions based on BST

B Tree, B+ Tree & Threaded binary tree
AVL Tree, Segment Tree
N-ary Tree and Problems

Discussion of Top product companies interview questions based on Advanced tree

Operations on Stack LIFO operation.
Applications & implementation of Stack Data Structure

Valid parenthesis, find next greater element, prefix, postfix etc

Complex problems of stack

Discussion of Top product companies interview questions based on Stack LIFO operation

Operations on Queue FIFO operation.
Applications & implementation of Queue Data Structure

Discussion of Top product companies interview questions based on Queue

Applications & implementation of Circular Queue Data Structure

Discussion of Top product companies interview questions based on Queue FIFO operation
Medium to Advanced set of problems discussion

Implementation of Priority Queue using various data structures
Insert, delete, peek operation in priority queue
Binary Heap Time Complexity of building a heap
Applications of Heap Data Structure

Min heap, Max heap implementation
Interview problems based on Min/Max Heap
Basic heap operation, Heapify operation implementation

Discussion of Top product companies interview questions based on Heap & Priority Queue

Hashing DS, Hash table, hash function.
Double hashing, probing
Insert, delete & search in hash in O(1) time

Top k elements, Smallest subarray, word count etc
Product companies Hashing interview questions

Implement LRU, various problems on LRU

Discussion of Top product companies interview questions based on Hashing

Graph and its representations.
Undirected Graph, Directed Graph, Connected Graph etc

Graph implementation of Adjacency List
Adjacency matrix representation of Graph

DFS implementation, Application
BFS implementation , Application

Medium to Advanced interview questions on BFS & DFS

All types & implementation of Shortest Path Algorithms
Single-Source Shortest Paths in Directed & Undirected graph

Trie Data Structure - Explained with Examples.
Why use Trie Data Structure?

Insert in Trie
Search in Trie
Trie Applications

Word search, Longest Common Prefix, Words in dictionary etc

Suffix Tree Introduction
Search a pattern using the built Suffix Array
Longest common prefix of two substrings
Finding the longest repeated substring
Pattern searching

Representation of ternary search trees
Applications of ternary search trees

Representation of Segment trees
Construction of segment tree from array
Interview questions of segment tree

Discussion of Top product companies interview questions based on Advanced DSA

Program Highlights

110+ Hours Live sessions
1:1 Doubt Session
4+ Projects
Multiple Batches Options
Life time accessibility
Job Referrals Program
Peer to peer Learning
Mock Interviews
Resume Preparation
Weekly Assignments
Regular Progress Tests
Code Explanation

Apply For DSA Classes

Success Stories

Course Feedback

What People Say

DSA Course Review

How it has helped them accelerate their careers to the next level.

🚀

Success Rate

👨‍💻

Placements

💰

Avg. Salary Growth

140% Growth

Siddharth Pande

Full Stack Developer

One of the Best Resources for Learning DSA & Design. Logicmojo Course helped me multiple times during interview preparation for companies like Walmart, Oracle and Microsoft.

Pre Logicmojo

Oracle

Post Logicmojo

…

295% Growth

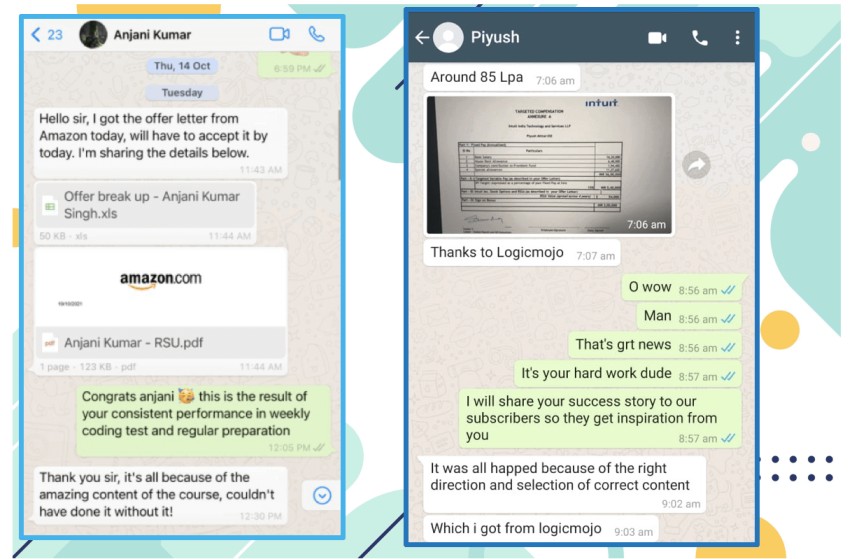
Anjani Kumar

Software Development Engineer II

Very well‑arranged course and amazing lecture delivery by trainers. The expert team is always available to solve any technical queries. Logicmojo live preparation helped me crack Zynga and now Amazon.

Pre Logicmojo

Zynga

Post Logicmojo

190% Growth

Afnaan Rafique

Software Engineer II

I had a great experience with Logicmojo. Learning by doing was exactly what I needed – the course has a big contribution to my success.

Pre Logicmojo

GlobalLogic

Post Logicmojo

…

170% Growth

Diwakar Choudhary

Staff Engineer / Manager

Excellent course for interview preparation – very straight to the point with in‑depth coverage in live classes, focusing on practical implementation of every coding & architectural problem.

Pre Logicmojo

Citrix

Post Logicmojo

…

270% Growth

Piyush Mittal

Senior Developer

The course curriculum is top‑quality and the learning experience outstanding. I cracked Paytm, Adobe, Intuit and finally joined Microsoft at 1.3 Cr LPA (MS IDC).

Pre Logicmojo

Paytm

Post Logicmojo

…

160% Growth

Priya Singh

Senior Software Engineer

Best‑quality curriculum with solid coding problems. Materials remain helpful even after the course.

Pre Logicmojo

MindTree

Post Logicmojo

…

210% Growth

Mohammed Shirhaan

Lead Engineer

Highly structured 7‑month program covering advanced coding & design concepts; helped me achieve my dreams.

Pre Logicmojo

Informatica

Post Logicmojo

…

210% Growth

Arpit Singh

Senior Software Engineer – I

Amazing classes – topics covered sequentially and the problem‑solving techniques are the best part of the course.

Pre Logicmojo

Post Logicmojo

…

130% Growth

Rajnish Kumar

Staff Engineer

Great course! Helped me understand algorithms deeply and implement solutions. Live courses are especially useful for working professionals.

Pre Logicmojo

Cred

Post Logicmojo

…

220% Growth

Aravindo Swain

Software Engineer – II

Concise, clear explanations from the trainer. Great quality online materials and classes covering all algorithm and system‑design interview problems.

Pre Logicmojo

Oracle

Post Logicmojo

…

Meet Our Mentors

Our DSA + System Design Course brings you industry experts from top tech companies who will guide you through your learning journey with real-world insights

Next Batch Starts from 15th June

Ranjan Kumar

Senior Developer at Amazon

Amazon

Experience

Teaching

Stony Brook

Ranjan is currently working at Amazon in Seattle, US. He has held senior developer roles at top product organizations, including Microsoft and Amazon. He is a well-known tutor on the internet. Ranjan completed his Master's degree at Stony Brook University. With over 5 years of teaching experience, Ranjan will be tutoring candidates for the upcoming batch starting on June 15th.

Sourav Karmakar

Senior AI Scientist

Amazon

Experience

Teaching

M.Tech (CS)

Indian Statistical Institute

Sourav Karmakar is a Senior AI Scientist at Intuit, where he develops GenAI solutions for QuickBooks Online. Previously at Amazon, he built large-scale ML models for fraud detection in ad traffic. At Fidelity Investments, he led AI initiatives using deep learning and NLP, including a patent-worthy project on document summarization. He holds an M.Tech in Computer Science from the Indian Statistical Institute and consistently ranked among top performers academically.

Mohamed Shirhaan

Senior Lead

WalmartLabs

Experience

Teaching

Corporate

Trainer

Shirhaan currently a Software Engineer III at Walmart Global Tech, with prior experience at Informatica where they contributed to building the Informatica Intelligent Cloud Services (IICS) as a Full Stack Engineer. Beyond corporate roles, they have actively mentored students through platforms like Newton School, GUVI, and Relevel, focusing on MERN stack and coding education for beginners. Their expertise spans React.js, Node.js, and cloud-based application development, combining industry impact with a strong commitment to tech education..

Sankalp Jain

Senior Developer

IIT Kharagpur

Senior

Role

Teaching

Graduate

IIT Kharagpur

Sankalp Jain, an IIT Kharagpur graduate, is a Senior Data Scientist with expertise in Computer Vision, LLMs, and vector databases. He built a virtual hairstyle try-on platform using BiSeNet and FastAPI, and developed "Knowledgebase," a Python API integrating Elasticsearch and Weaviate. As an instructor at AlmaBetter and Logicmojo, he has mentored over 2,100 students in ML, statistics, and real-world projects. His work spans startups like ODIN AI to global roles at Turing and Publicis Sapient.

Ravi Singh

Senior Architect

WalmartLabs

14+

Experience

Teaching

Corporate

Trainer

Ravi has over a decade of experience spanning Amazon, Cisco, and Walmart Global Tech, where they architected scalable systems and optimized enterprise performance. At Walmart, they improved a production system’s performance by 300% and implemented core modules using Java, Spring Boot, Redis, and Vert.x. At Cisco, they worked on cloud orchestration and backend services for wireless controllers. At Amazon, they contributed to AWS by scaling systems to index millions of products and automate business decisions using large-scale data processing.

Head Instructor

Demo Class

Experience our teaching methodology and course content before you enroll

Free Demo Class

Join our free demo session to experience the learning environment and get all your questions answered by our expert instructors.

Introduction to DSA and System Design concepts

Meet our instructors and mentors

Get all your queries addressed

Schedule a Call

Ready to Start Your Journey?

Join our upcoming batch starting on June 15th and learn from the best in the industry. Limited seats available!

Enhanced your salary 8X just by learning from DSA & System Design Course

High demand for software developer profile across all product companies in the world

Just Few Months Of Preparation in Live Classes and Crack Coding & System Design Rounds in Top Product Based Companies

25,12,290

Average Annual
Base Salary (2025)

85%

Average Salary Growth Annual
(Service Companies --> Top Product Companies)

161%

Software Developer
Job Listings Growth,
Annual (2019-2025)

Career Impact

Software Development Engineer(SDE) Roles have Average package of 25+ Lakh in Top Product Based Companies.

Learn from MAANG companies
Experts & Transform your Career

Apply For Live Classes

Course Steps ?

Learn Data Structures, Algorithms, Problems Solving techniques & System Design from scratch

How to get placed in product companies

Attend free demo class
from your mentor

Just click on Free Trial
for attending demo class

Join the
course

Talk to our Experts for any queries and join the course

Attend live sessions
regularly

Attend sessions regularly and
complete all assignments

Get Job assistance and
certification

Get job assistance & certification
after completion of the course

Job Focused Live interactive sessions to help realize your dreams

Learn and get hired in simple steps - DSA Course Roadmap

Acquire Expertise

Learn Data Structures, Algorithms & problem-solving techniques from industry veterans in a Live session and enjoy an immersive learning experience.
Missed your classes

If you miss any classes, No problem. Just after every class, you will get video access to all classes for lifetime access.
1:1 doubt clearing sessions

Attend the Live 1:1 doubt clearing sessions/mentorship sessions.
In case you missed asking doubts in classes, attend separate 1:1 doubts solving classes
Assignments for practice

Learn DSA from practice. Get assignments from the mentor for self attempt

Flexible batches

Attend multiple batches with multiple trainers. If you missed any session or topics, attend any batches as per your flexibility. Even after course completion, you can repeat any classes for 1 year.
Job assistance program

Be attentive with regular classes & solve all assignments. After completion of the course, you will be eligible for the job referrals program
Mock Interview sessions

Be attentive with regular classes & solve all assignments. After completion of the course, you will be eligible for the mock interview session
Peer to Peer Learning

Slack group for peer-to-peer learning & discussion with batchmates. Hackerrank for 1:1 tests & GitHub for Code review

Job Focused Programs to help realize your dreams

Learn and get hired in simple steps - Self Paced Course

Acquire Expertise

self-paced course to learn Data Structures, algorithms & system design from industry veterans and enjoy an immersive learning experience.
Revise concepts with Assignments

Practice assignments in an editor, Can't solve it? All assignments also have detailed explanations.
Ask your Doubts Anytime

Getting Stuck While Coding? Get all your doubts resolved.
Ask any queries in any lectures as well as assignments from experts

Online weekly coding env

Check your progress & feel the competitive environment every week with an online coding test.
Job assistance

Get ready for the final battle? All consistent performers in the weekly test will get referrals in tech company's interviews.
Code Execution environment

We have integrated an online code execution environment editor for practicing all lectures & assignments with test cases & solution

Apply For Live Classes

Course Fee?

DSA + System Design Course Fee

Total Fee

₹ 45,000

No Cost EMI

As low as ₹ 3,750/month

Request a Call

We have partnered with the following financing companies to provide competitive finance options at 0% interest rate with no hidden costs.

DSA + System Design Course Duration

Duration: 7 months Live Weekend Classes
Prerequisite : Basic understanding of programming required
Complete Interview Preparation Course

Who can apply for the DSA + System Design Classes?

Software engineers
IT Professionals
Managers
Architect
Senior Developers

Apply For Live Classes

Hear Directly From Our Global Community

Real reviews from across the web. We believe in full transparency—see what developers, career-switchers, and tech leaders are saying about their experience with LogicMojo.

Excellent

4.8

Based on 1,200+ reviews

Few Reviews From Subscribers

Over Chat, Email, And Linkedin

Our subscribers create milestones by cracking top tech companies' interviews & grab more than 80+ LPA(Lakh Per Annum) package in India . Logicmojo course provides them the guidance, direction, concepts & well-structured content to help them during their preparation.

These are a few of the reviews of our subscribers.

Course Reviews

Logicmojo in
the News

Logicmojo Awards
& Affiliation

Data Structures and Algorithms (DSA) Free Tutorial

Frequently Asked Questions

Everything you need to know about the courses, tuition fees, and more.

+ What topics are covered in a DSA course?

Course Content

Data Structures and Algorithms (DSA) course typically covers a variety of topics that are fundamental to computer science and programming. These concepts form the building blocks for solving complex computational problems efficiently.

Fundamentals

Basic concepts and building blocks
Algorithm analysis and complexity
Time and space complexity metrics
Big O notation and efficiency analysis

Basic Data Structures

Arrays (static, dynamic, multi-dimensional)
Linked Lists (singly, doubly, circular)
Stacks & Queues implementations
Priority queues and circular queues

Advanced Data Structures

Trees (binary, BST, AVL, Red-Black)
Tree traversal techniques
Graphs and representation methods
Hash tables and collision resolution

Searching & Sorting

Searching algorithms (linear, binary, interpolation)
Basic sorting (bubble, selection, insertion)
Advanced sorting (merge, quick, heap)
Specialized sorting (counting, radix sort)

Graph Algorithms

Graph traversals (BFS, DFS)
Shortest paths (Dijkstra, Bellman-Ford)
Minimum spanning trees (Prim, Kruskal)
Graph coloring and cycle detection

Algorithmic Techniques

Recursion (factorial, Fibonacci, Tower of Hanoi)
Dynamic Programming (memoization, bottom-up)
Greedy Algorithms (fractional knapsack, Huffman)
Backtracking (N-Queens, Hamiltonian cycle)
Divide and Conquer (merge sort, Strassen's)

These topics build the foundation for designing and analyzing efficient algorithms to solve complex computer science problems. Understanding DSA thoroughly is essential for excelling in coding interviews and developing optimized software solutions.

View Detailed Syllabus Watch Sample Class Ask More Questions

+ Which language is best for learning DSA?

DSA concepts are language-agnostic. We teach using Java, JavaScript, C++ and Python—pick whichever you’re most comfortable with.

+ How long does it take to complete a DSA course?

Logicmojo’s DSA course is offered in two formats:

7-month program: Live DSA classes for 4 months, then 3 months of System Design.
4-month program: Intensive live classes focused solely on DSA.

+ Why is learning Data Structures and Algorithms important?

All top tech companies test candidates on DSA to gauge problem-solving skills. It’s the cornerstone of computer science applied across e-commerce, finance, health tech, telecom, and more.

Our DSA course combines lectures for conceptual clarity with assignments for hands-on practice in real-world problem solving.

+ Who should take this DSA course?

A DSA course can benefit a wide range of learners. In particular:

CS students building a strong foundation.
Aspiring software developers preparing for interviews.
IT professionals upskilling to solve complex problems.
Competitive programmers (ICPC, LeetCode, Code Jam).
Job seekers in tech—Google, Amazon, Facebook, etc.
Educators & mentors teaching programming concepts.

Overall, anyone serious about coding efficiency and career growth should master DSA.

+ Eligibility to join this DSA course

Working IT professionals targeting product:contentReference[oaicite:0]{index=0}.

+ Can a non-IT or non-CS graduate join?

Yes—our course starts from first principles, enabling non-CS backgrounds to build DSA skills from scratch.

+ How does the placement process work?

After course completion, you’ll:

Step 1: Take mock DSA interviews to gauge readiness.
Step 2: One-on-one resume prep with our experts.
Step 3: Job referrals and interview scheduling with top product companies.

+ How many mock interviews can I attempt?

As many as you need—our goal is to ensure you’re fully prepared for real company interviews.

+ Is there a timeline for mock interviews?

We recommend finishing mocks within 6 months of course end, but you can extend up to 1 year in special cases.

+ Which companies are considered for placements?

We partner with top product firms across India—your referrals can land you interviews at the likes of Google, Amazon, Flipkart, and more.

+ When will I receive the DSA certificate?

Once you successfully complete the course, you’ll receive both course-completion and project-completion certificates.

+ What projects are covered in the DSA course?

The 7-month DSA program includes real-world backend architectures and system designs. Key components:

Design Patterns: In-depth coverage and real-world applications.
Business Logic: Writing clean, bug-free code for project requirements.
Distributed Systems: Microservices, Kafka, sharding and cloud infra design.

+ How many projects are included?

We start simple and ramp up complexity. On average, four projects are completed to strengthen your portfolio.

+ Which languages are used for projects?

You may choose any OOP language—Java, Python, JavaScript or C++—for your projects.

+ What is the fee for the DSA course?

7-Month DSA + System Design: INR 52,000/- (15% off for first 15 students: INR 45,000/-)

4-Month DSA Only: INR 32,000/- (15% off for first 15 students: INR 27,000/-)

+ Can I pay using No Cost EMI?

Yes—choose from 3, 6, 9 or 12-month interest-free EMI plans via any credit card.

Still have questions?

If you couldn't find the answer to your question, feel free to reach out to our team. We're here to help!

Duration	Total Amount	Monthly Payments
NO COST EMI	12 Months	₹1,10,000 +18% GST	₹10,816
Standard Interest Rates Applicable	18 Months	₹1,10,000 +18% GST	₹7,211

Advanced Data Structures Algorithms & System Design(HLD+LLD) by Logicmojo

DSA System Design Course LIVE

Data Science and AI Course LIVE

Self Paced Course

Become an Expert with Logicmojo DSA Course

Our Alumni Are Hired by Top Tech Giants

Become an Expert with Logicmojo DSA Course

Master Data Structures & Algorithms with Logicmojo DSA Course

Our students have gotten job offers from:

Our placement success rate

1. Course Curriculum

Learn from Experts

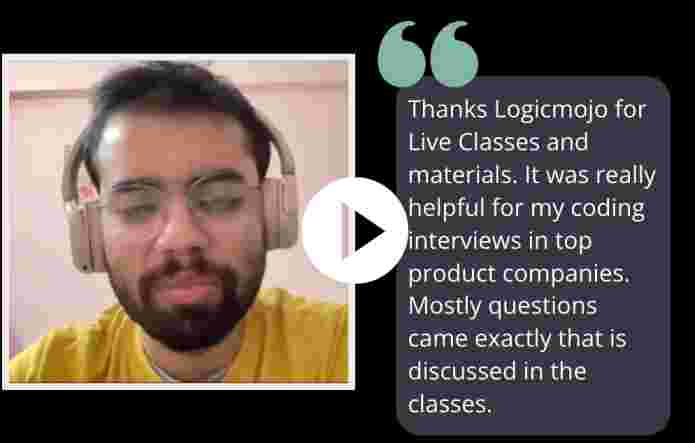
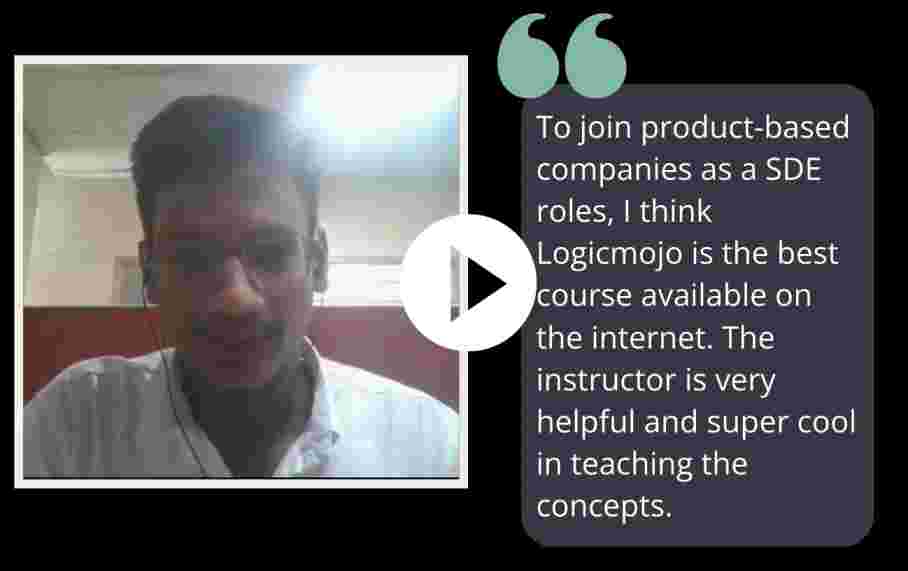
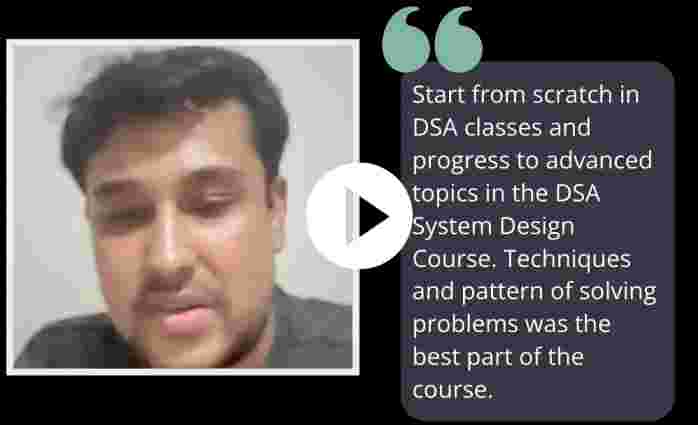
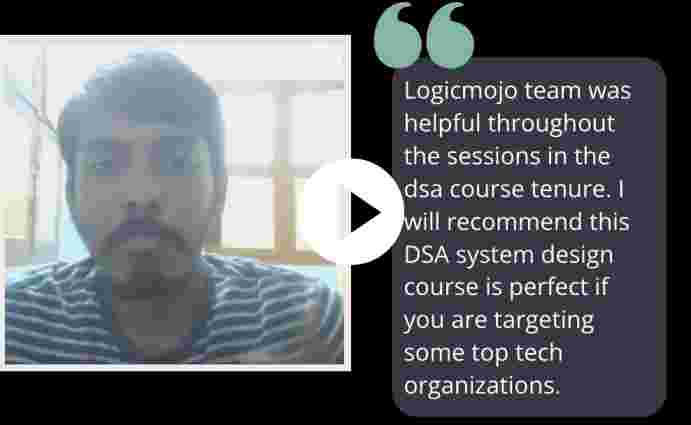
Live Interactive Sessions

Competitive Coding Tests

Collaborative Learning

Gain Real-World Experience

Practical Experience through Projects

Authoritative Job Assistance

Your Trustworthy Support System

1:1 Doubt Clearing Sessions

Lifetime Access & Updates

Transparent & Flexible Pay

Curriculum Deep-Dive

Data Structures

Algorithms

2. About Online DSA Course

See Your Transformation

From College to a Top Company

Key Outcomes:

From Service to Product-Based

Key Outcomes:

From Manager to Tech Visionary

Key Outcomes:

Frequently Asked Questions

What important skills will I learn?

What are the prerequisites for this course?

What job opportunities are available after this course?

The Complete Journey

Beyond The Code

Module Goal

Module Overview

Key Topics Covered:

Student Placement Statistics

Average Salary Hike

Highest CTC Secured

Alumni Placed

Request a Callback

Request Received!

Your DSA & System Design Journey

First 4 Months: Data Structures & Algorithms

Time Complexity

Array, String and Linked List

Stack and Queue

Hashing & Heap Sort

OOD Concepts

Competitive Programming

Binary Tree, N-ary Tree, Segment Tree etc

Greedy Algorithm

Backtracking & Recursion

Graph Theory

Dynamic Programming

Advanced Data Structures

Next 3 Months: System Design

System Design Basics

Distributed System Basics

Cloud Architecture Deployment

Design Patterns

SQL & NoSQL

Kubernetes, Docker Deployment

Distributed Cache, Database Sharding

Microservice Architectures Details

Big Data, Hadoop Kafka, Zookeeper

Scalable System Design Problems Discussion

High level Design(HLD) + LLD(Low Level Design)

System Design Interview Questions

4. DSA Courses

5. DSA Course Complete Syllabus

Module 1: System Design Basics & Approach

Module 2: Distributed Database & SQL

Module 3: Load Balancer, Cache & CDN

Advanced
Data Structures Algorithms & System Design(HLD+LLD)
by Logicmojo