The knowledge of Data Structures and Algorithms forms the basis for identifying programmers, giving yet another reason for tech enthusiasts to get upscaled. While data structures help in the organization of data, algorithms help find solutions to the unending data analysis problems.
So, if you are still unaware of Data Structures and Algorithms in Python, here is a detailed article that will help you understand and implement them.
Before moving on, take a look at all the topics discussed in over here:
📚Built in Data Structures
🔧User defined Data Structures
⚙️What are Algorithms?
📈Elements of a Good Algorithms
🔄Sorting Algorithms
🔍Searching Algorithms
Introduction to Data Structures And Algorithms in Python
In-built Data Structures:

✔Lists: This is the most versatile data structure in Python and is written as a list of comma-separated elements enclosed within square brackets. A List can consist of both heterogeneous and homogeneous elements. Some of the methods applicable on a List are index(), append(), extend(), insert(), remove(), pop(), etc. Lists are mutable; that is, their content can be changed, keeping the identity intact.
✔Tuples: Tuples are similar to Lists but are immutable. Also, unlike Lists, Tuples are declared within parentheses instead of square brackets. The feature of immutability denotes that once an element has been defined in a Tuple, it cannot be deleted, reassigned or edited. It ensures that the declared values of the data structure are not manipulated or overridden.
✔Dictionaries: Dictionaries consist of key-value pairs. The 'key' identifies an item, and the 'value' stores the value of the item. A colon separates the key from its value. The items are separated by commas, with the entire thing enclosed within curly brackets. While keys are immutable (numbers, Strings or Tuples), the values can be of any type.
✔Sets: Sets are an unordered collection of unique elements. Like Lists, Sets are mutable and written within square brackets, but no two values can be the same. Some Set methods include count(), index(), any(), all(), etc.
User-defined Data-structures And Algorithms in Python:
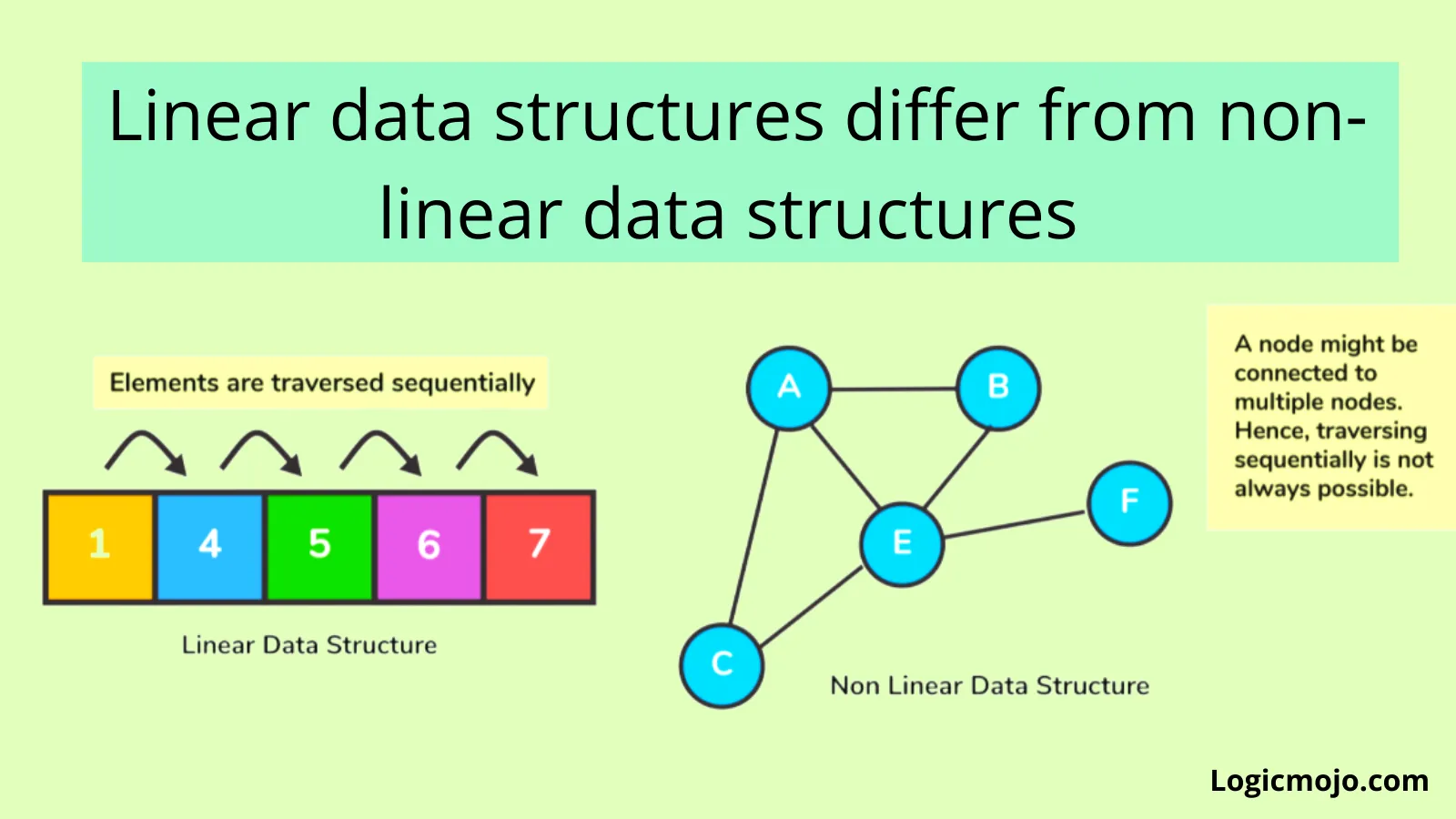
Linear Data Structures
Linear data structures in python are those whose elements are in sequential and in ordered way. For example: Linked list, Stack, Queue
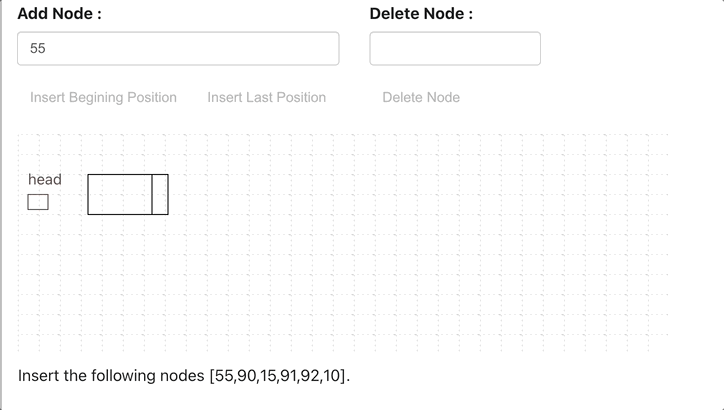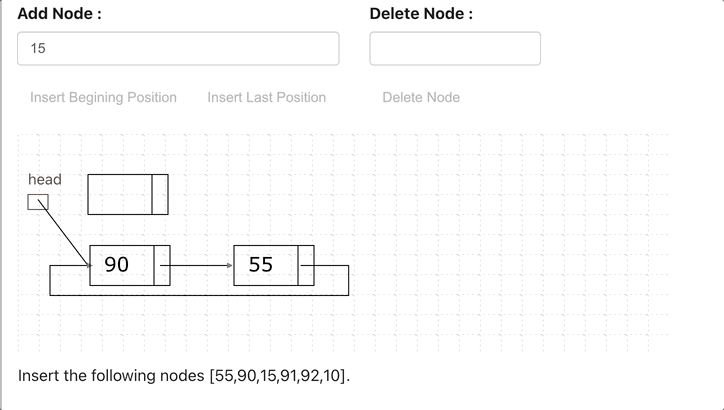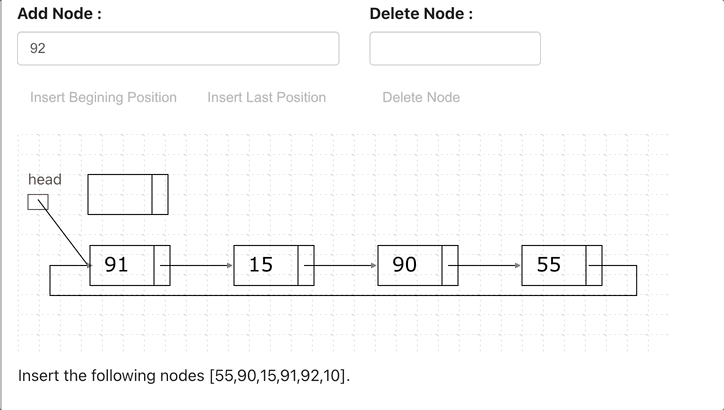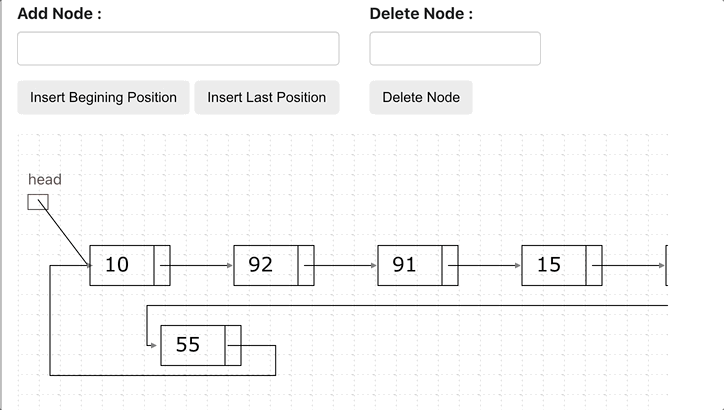
Linked List in Python
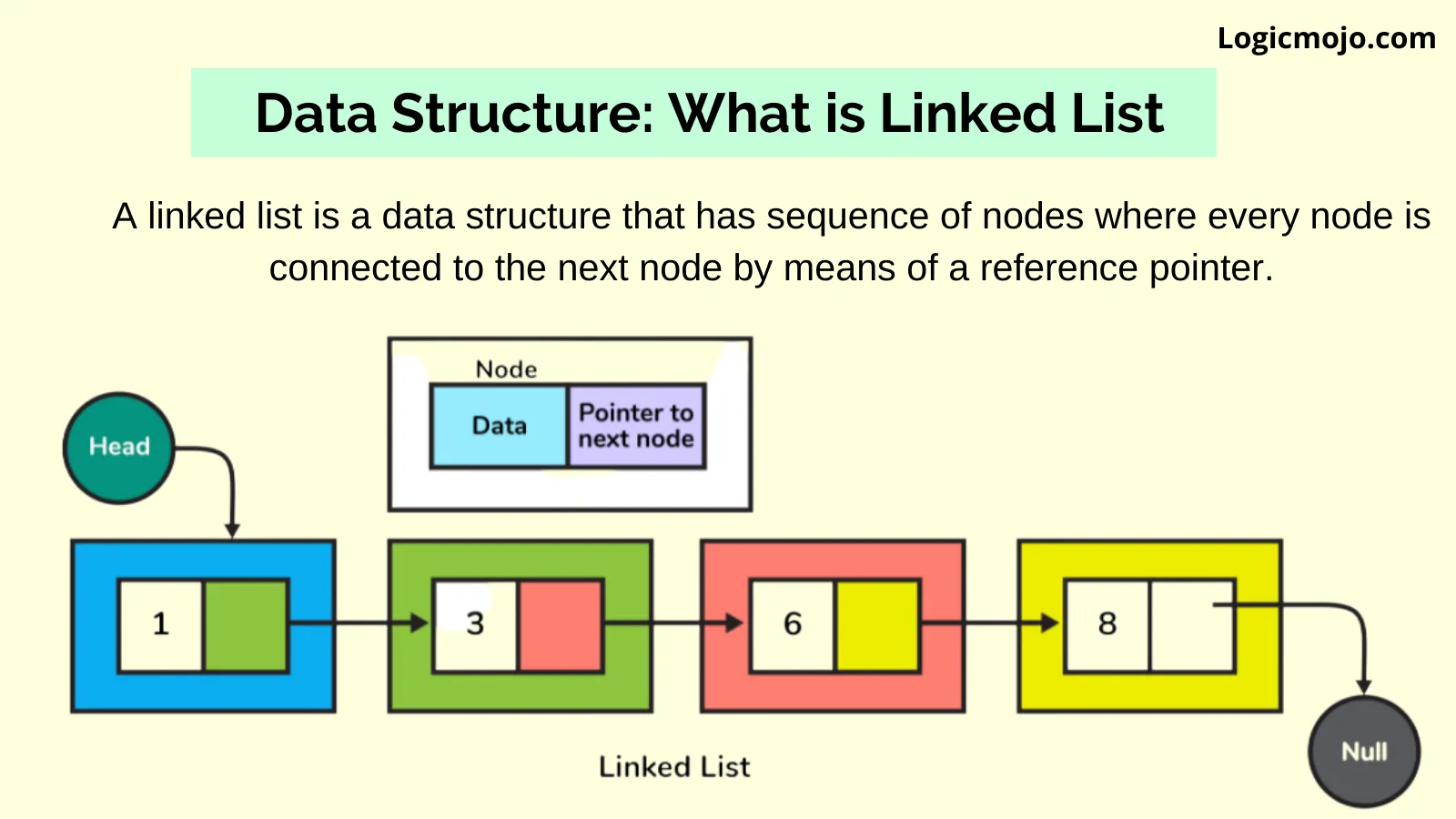
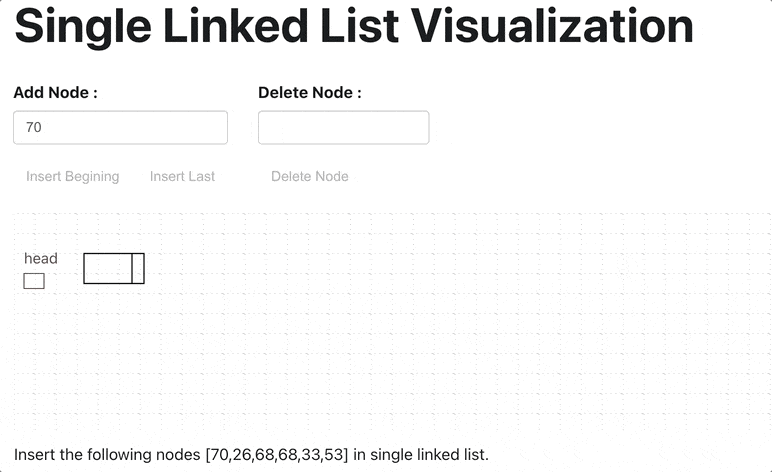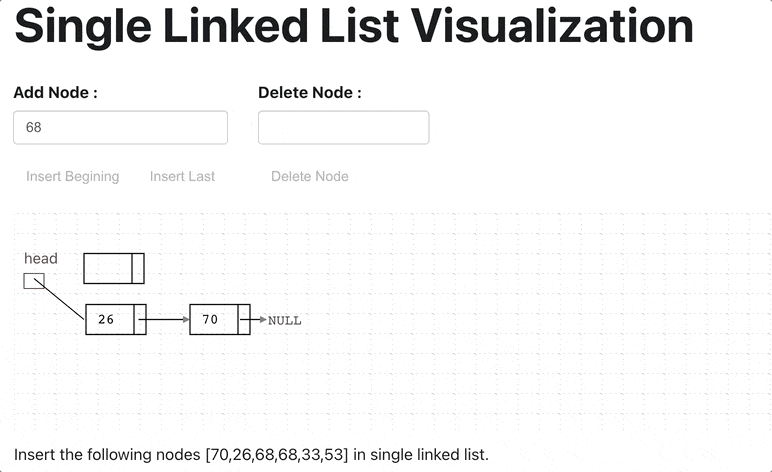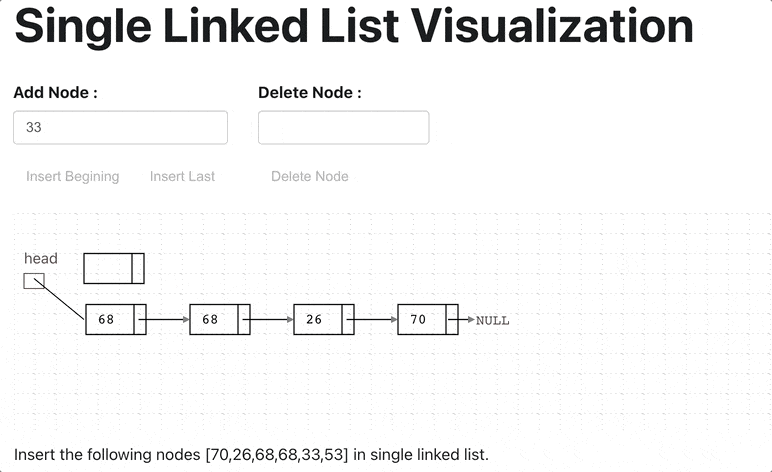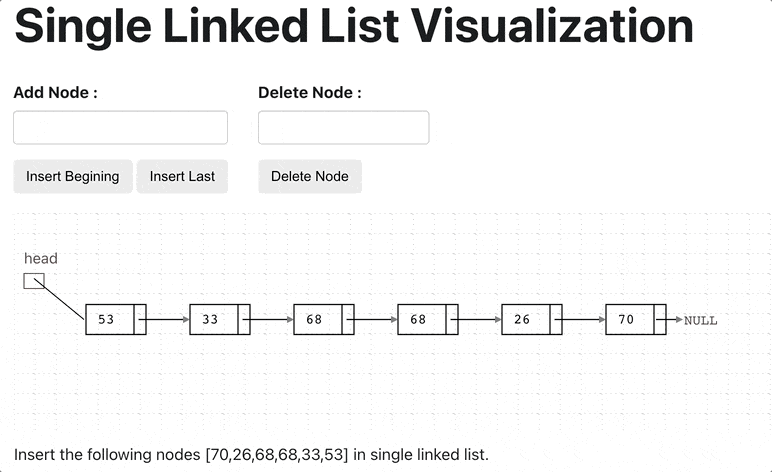
A linked list is a linear data structure with the collection of multiple nodes, where each element stores its own data and a pointer to the location of the next element. The last link of linked List points to null.
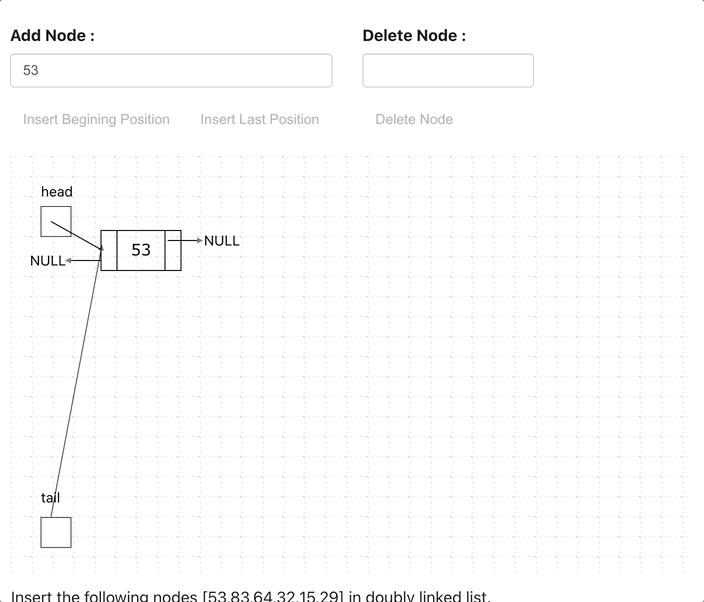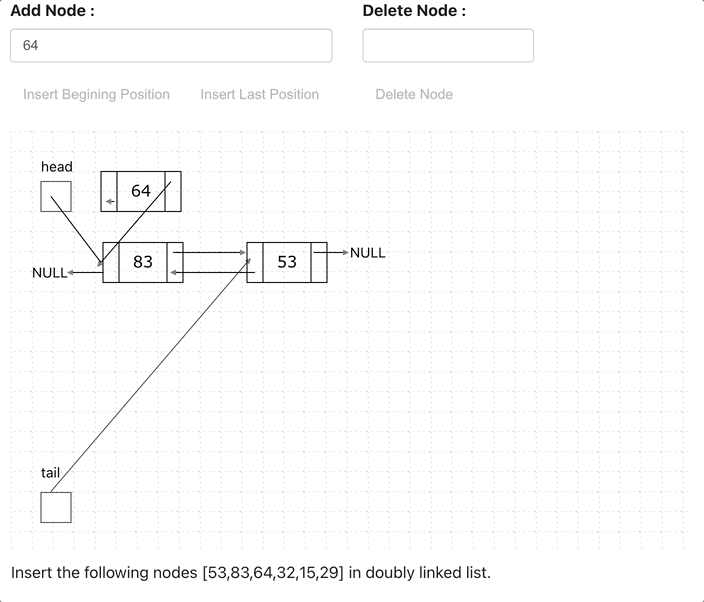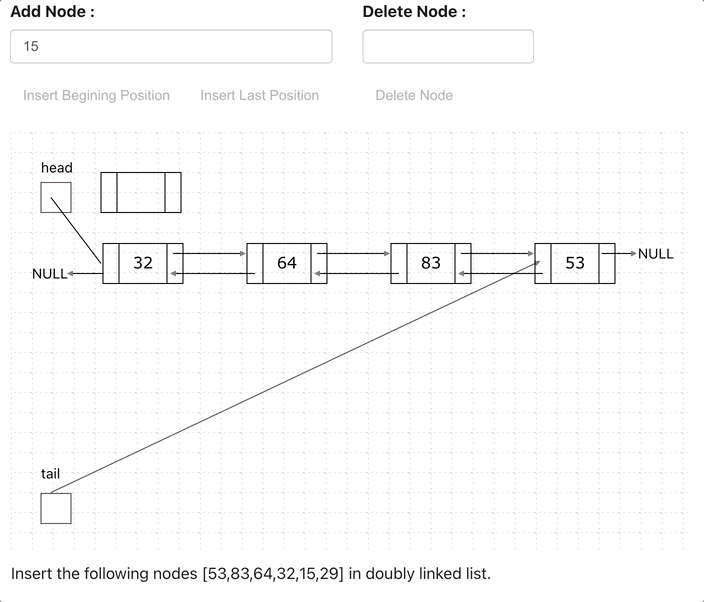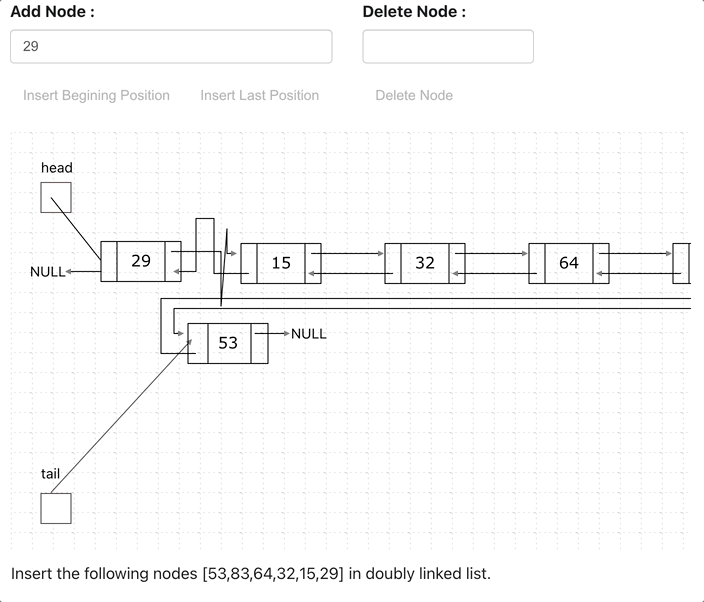
An element in Linked List is called node. The first node is called head. The last node is called tail.
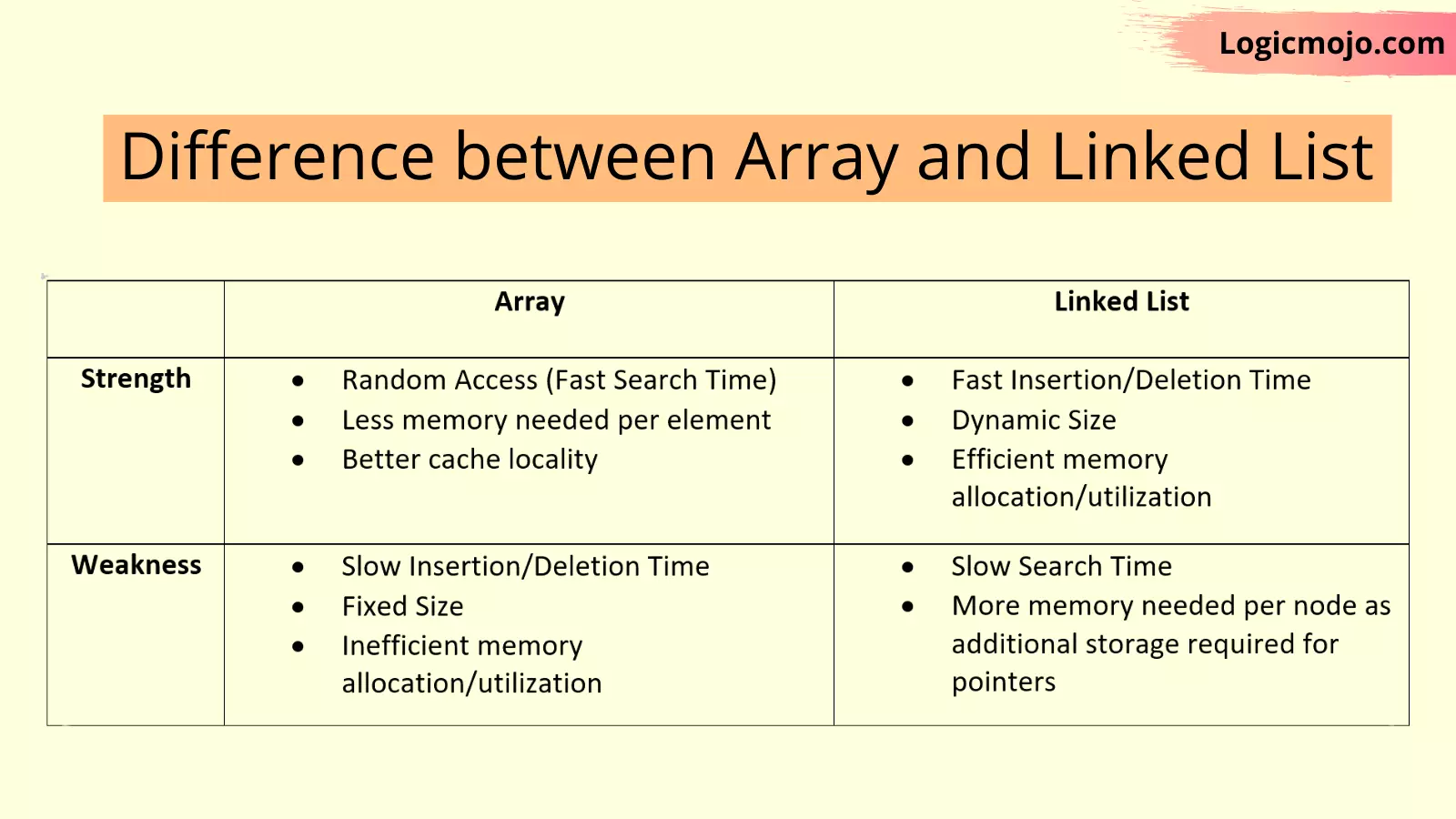
Types of Linked List
Singly Linked List (Uni-directional)
The singly linked list is a linear data structure in which each element of the list contains a pointer which points to the next element in the list. Each node has two components: data and a pointer next which point to the next node in the list.
# Node class
class Node:
# Function to initialize the node object
def __init__(self, data):
self.data = data # Assign data
self.next = None # Initialize
# next as null
# Linked List class
class LinkedList:
# Function to initialize the Linked
# List object
def __init__(self):
self.head = None
Doubly Linked List (Bi-Directional)
Doubly Linked List is just same as singly Linked List except it contains an extra pointer, typically called previous pointer, together with next pointer and data.
# Node of a doubly linked list
class Node:
def __init__(self, next=None, prev=None, data=None):
self.next = next # reference to next node in DLL
self.prev = prev # reference to previous node in DLL
self.data = data
Advantages over singly linked list
✔A DLL can be traversed in both forward and backward direction.
✔The delete operation in DLL is more efficient if pointer to the node to be deleted is given.
Circular Linked List
A circular linked list is a variation of a linked list in which the last node points to the first node, completing a full circle of nodes. You can say it doesn't have null element at the end.
Application of Circular Linked List
✔The real life application where the circular linked list is used is our Personal Computers, where multiple applications are running. All the running applications are kept in a circular linked list and the OS gives a fixed time slot to all for running. The Operating System keeps on iterating over the linked list until all the applications are completed.
✔Another example can be Multiplayer games. All the Players are kept in a Circular Linked List and the pointer keeps on moving forward as a player's chance ends.
✔Circular Linked List can also be used to create Circular Queue. In a Queue we have to keep two pointers, FRONT and REAR in memory all the time, where as in Circular Linked List, only one pointer is required.
Stacks in Python
What is Stack?
Stack, an abstract data structure, is a collection of objects that are inserted and removed according to the last-in-first-out (LIFO) principle. Objects can be inserted into a stack at any point of time, but only the most recently inserted (that is, "last") object can be removed at any time.
Listed below are properties of a stack:
✔It is an orderd list in which insertion and deletion can be performed only at one end that is called the top.
✔Recursive data structure with a pointer to its top element.
✔Follows the last-in-first-out (LIFO) principle
Stack Concepts
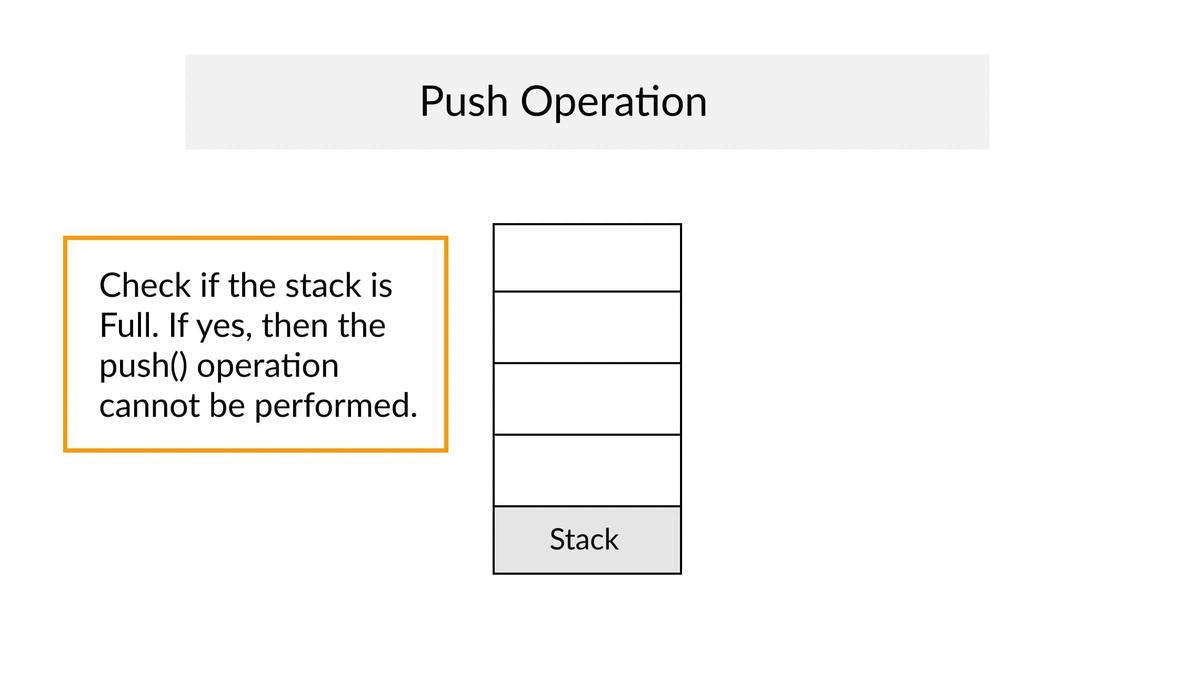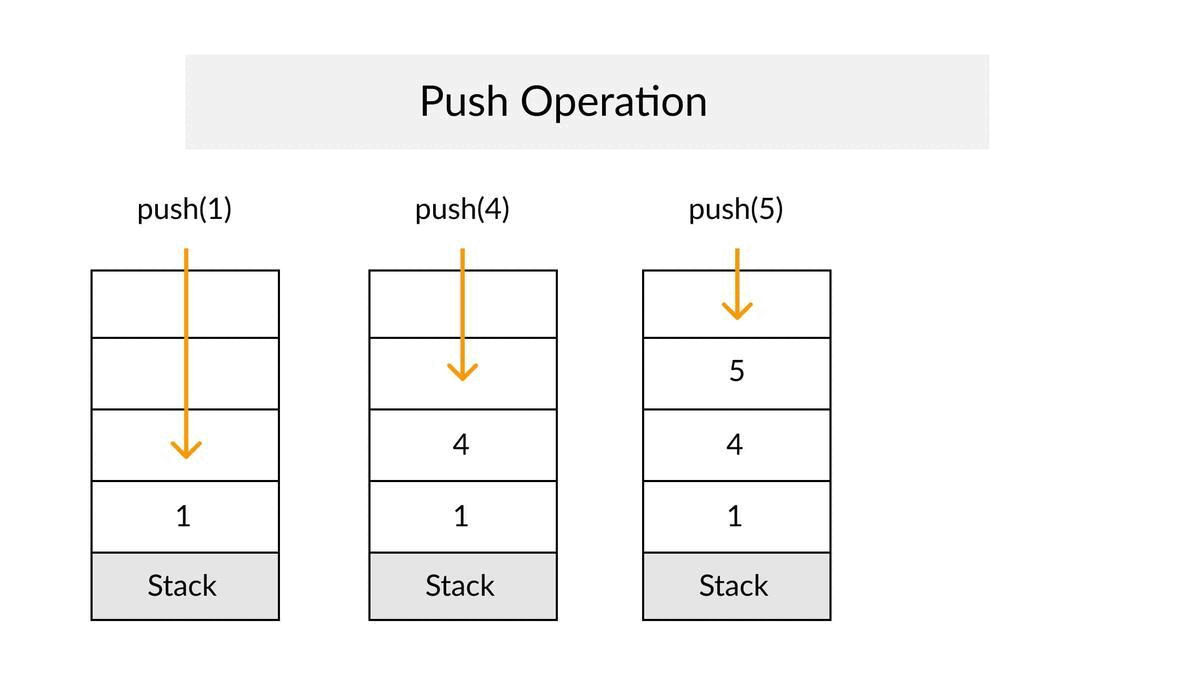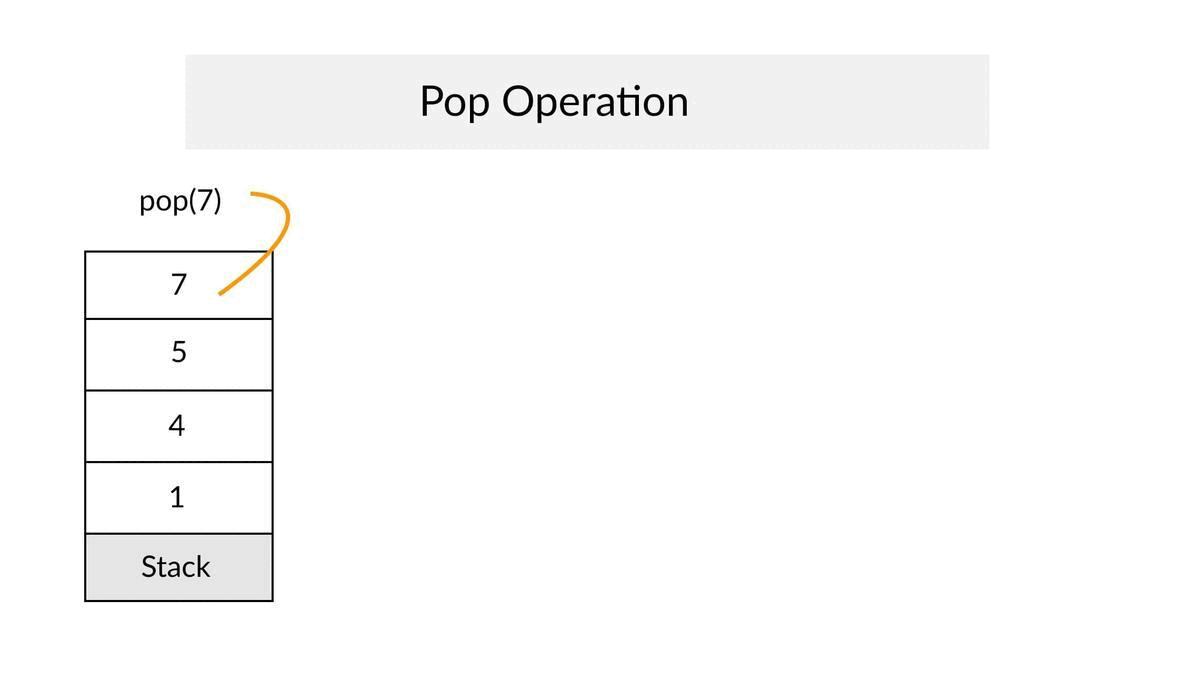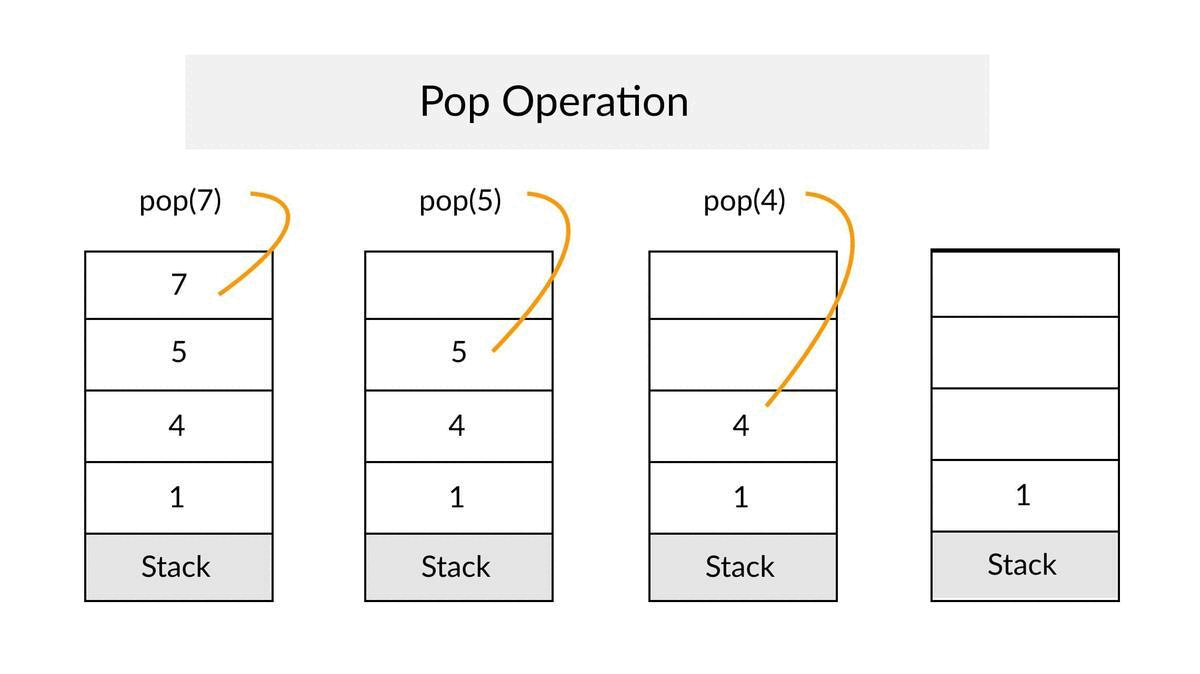
✔When an element is inserted in a stack, the concept is called a push.
✔When an element is removed from the stack, the concept is called pop.
✔Trying to pop out an empty stack is called underflow (treat as Exception).
✔Trying to push an element in a full stack is called overflow (treat as Exception).
Applications of Stack
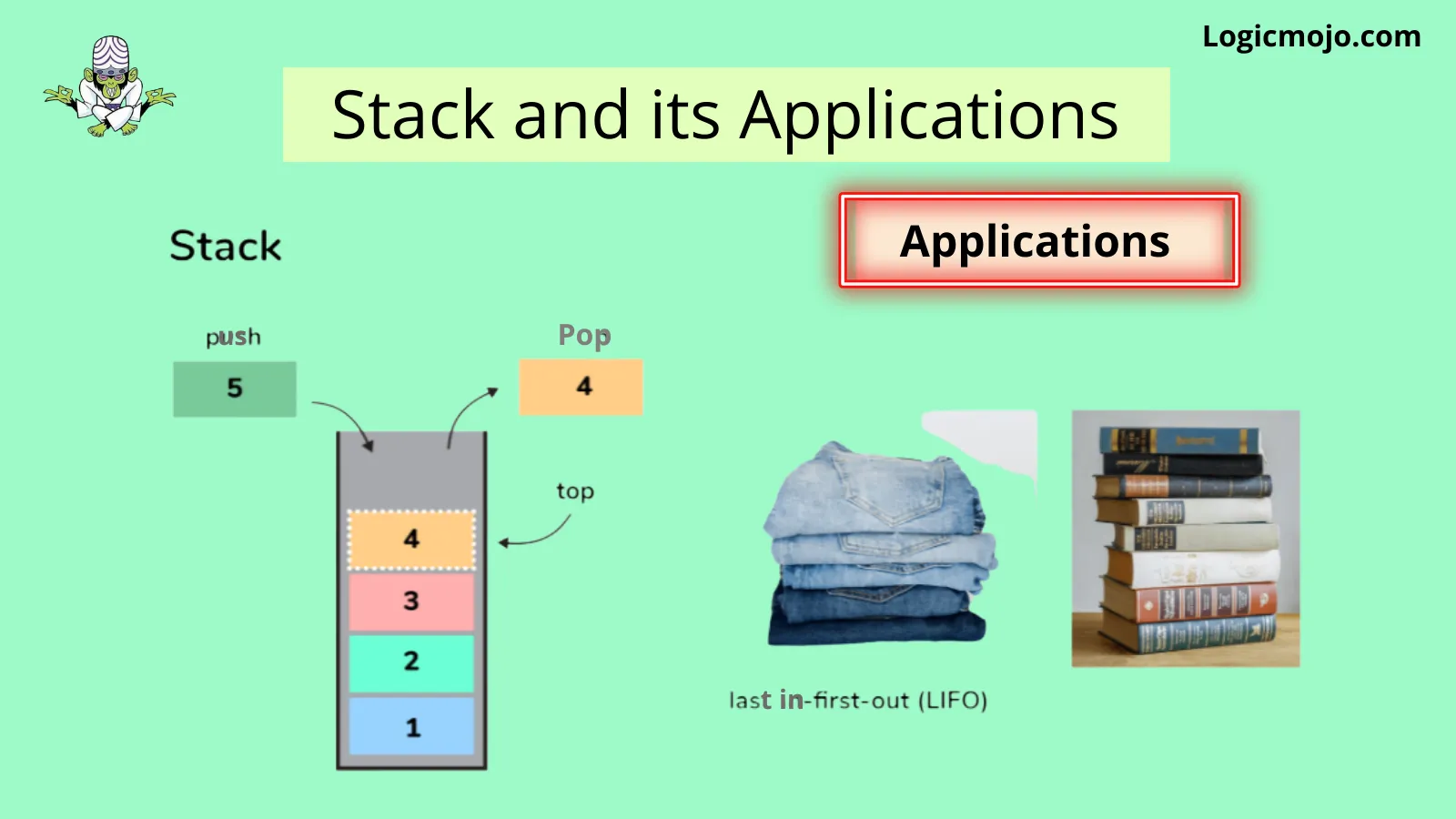
Following are some of the applications in which stacks play an important role.
✔Balancing of symbols
✔Page-visited history in a Web browser [Back Buttons]
✔Undo sequence in a text editor
✔Finding of spans (finding spans in stock markets)
Stack Implementation using List
Push Operation
✔Write a class called Stack.
✔We have to maintain the data in a list. Let's add an empty list in the Stack class with name elements.
✔To push the elements into the stack, we need a method. Let's write a push method that takes data as an argument and append it to the elements list.
class Stack:
def __init__(self):
self.elements = []
def push(self, data):
self.elements.append(data)
return data
Pop Operation
✔Similarly, let's write the pop method that pops out the topmost element from the stack. We can use the pop method of the list data type.
class Stack:
## ...
def pop(self):
return self.elements.pop()
Complexity Analysis
Let n be the number of elements in the stack. The complexities of stack operations with this representation can be given as:
✔Time Complexity of push() O(1)
✔Time Complexity of pop() O(1)
✔Space Complexity O(n)
Queues in Python
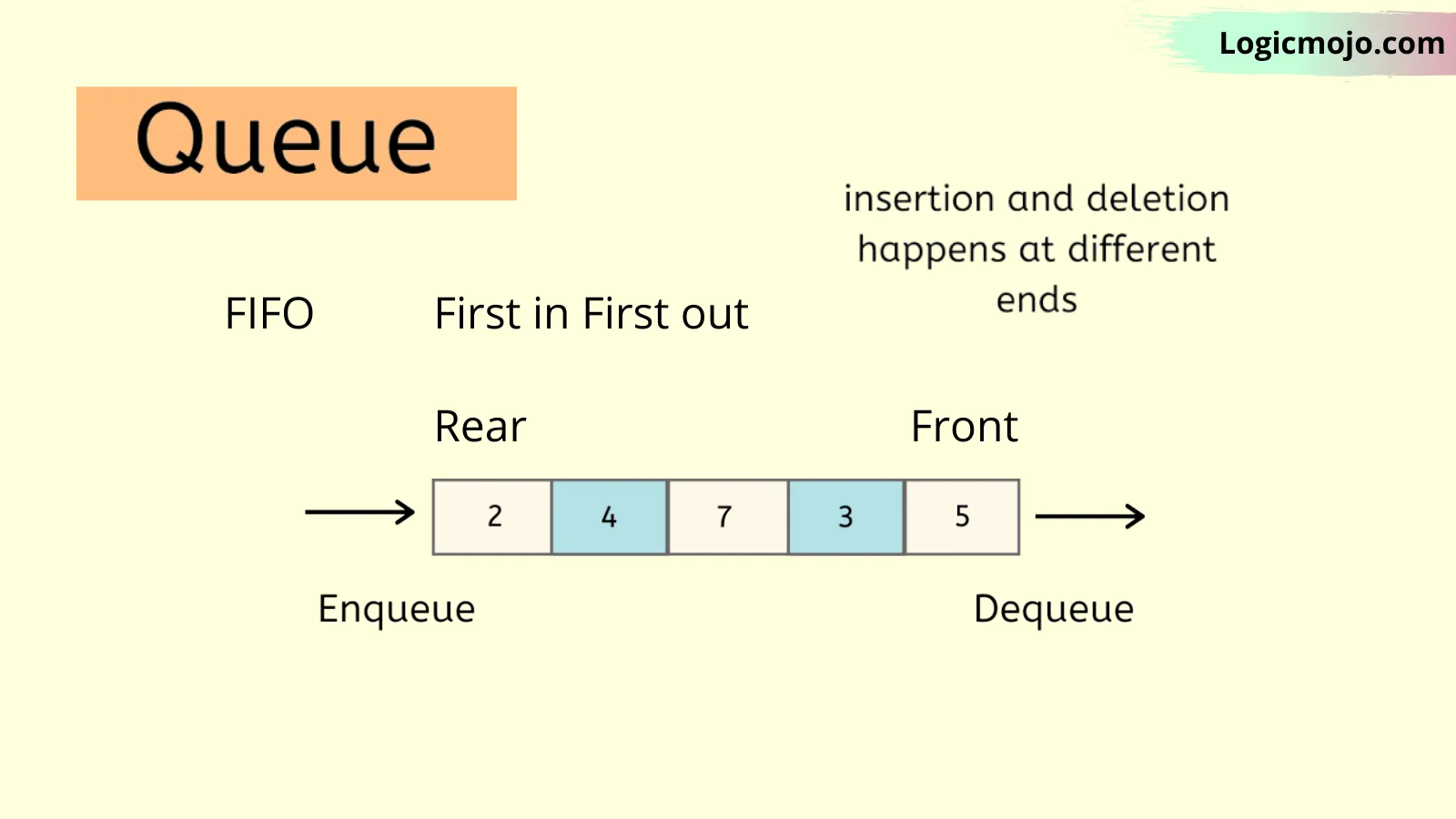
Queues are also another type of abstract data structure. Unlike a stack, the queue is a collection of objects that are inserted and removed according to the first-in-first-out (FIFO) principle.
Listed below are properties of a queue:
✔Often referred to as the first-in-first-out list
✔Supports two most fundamental methods enqueue(e): Insert element e, at the rear of the queue dequeue(): Remove and return the element from the front of the queue
Queue Concepts
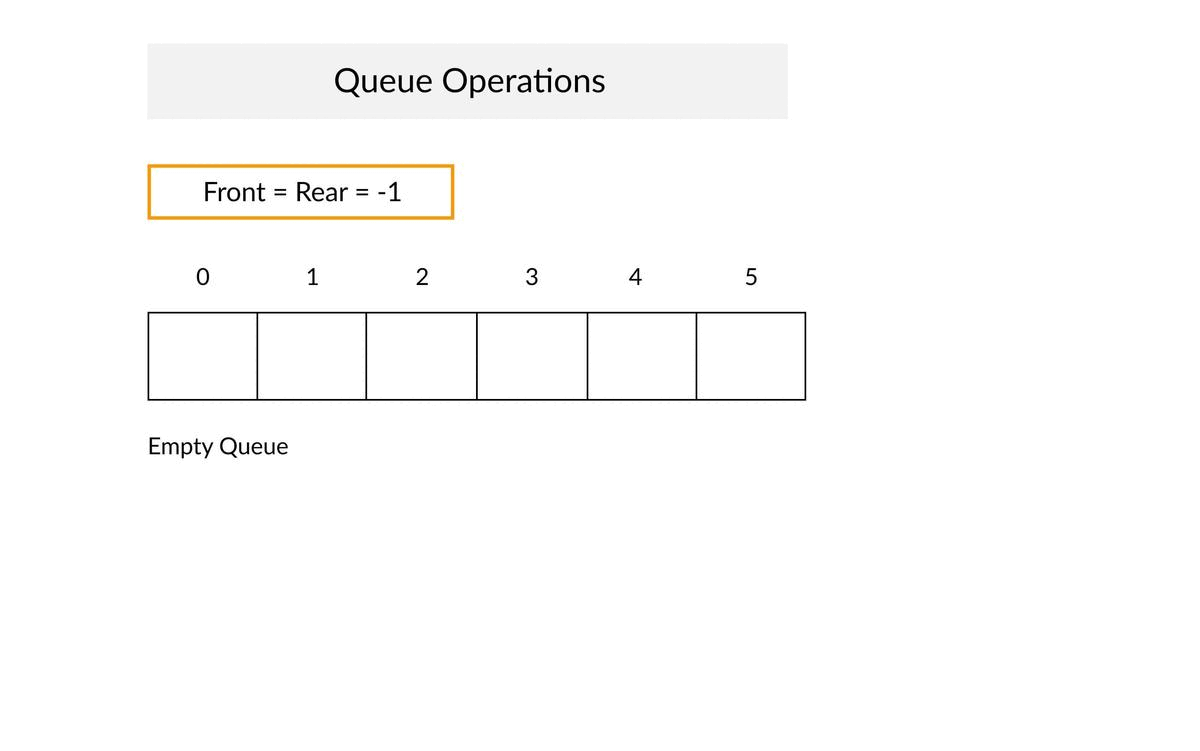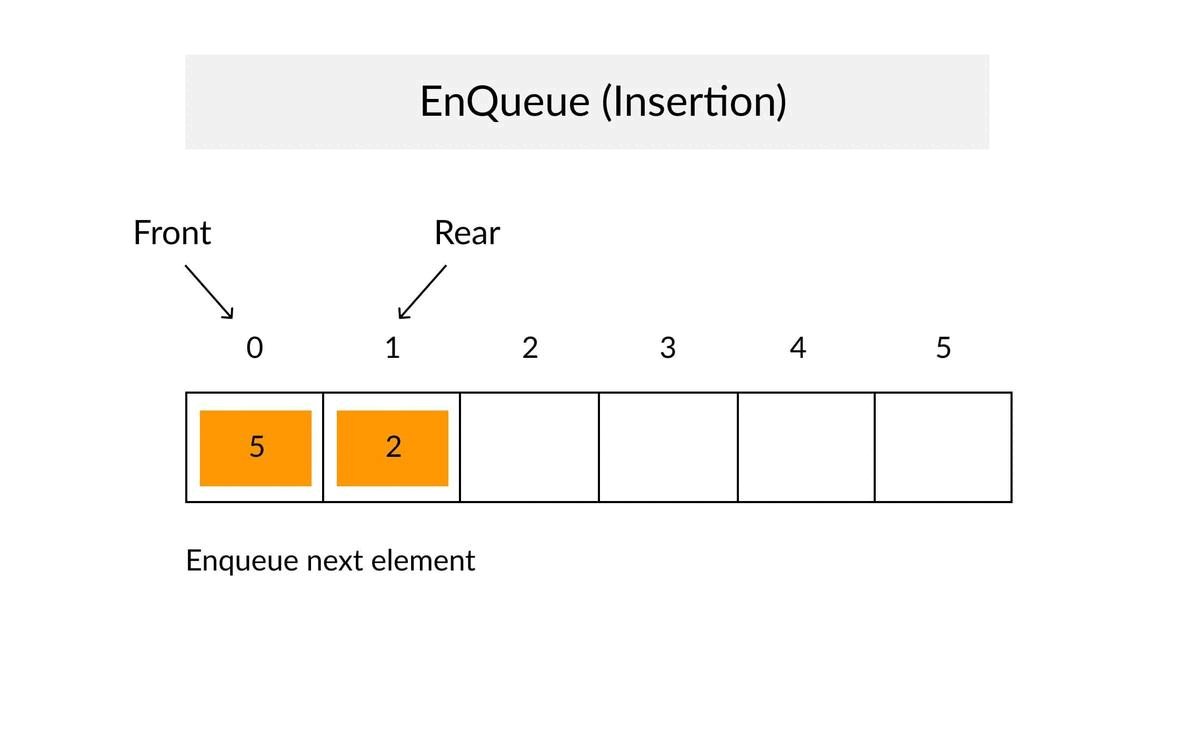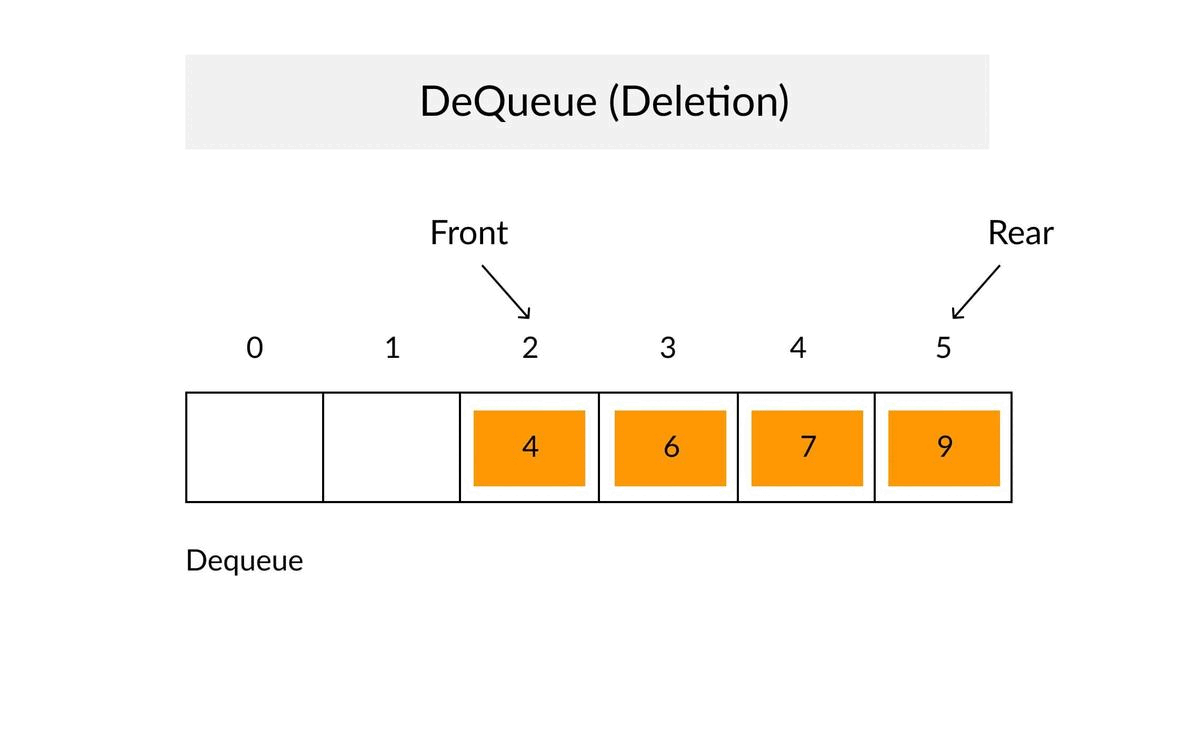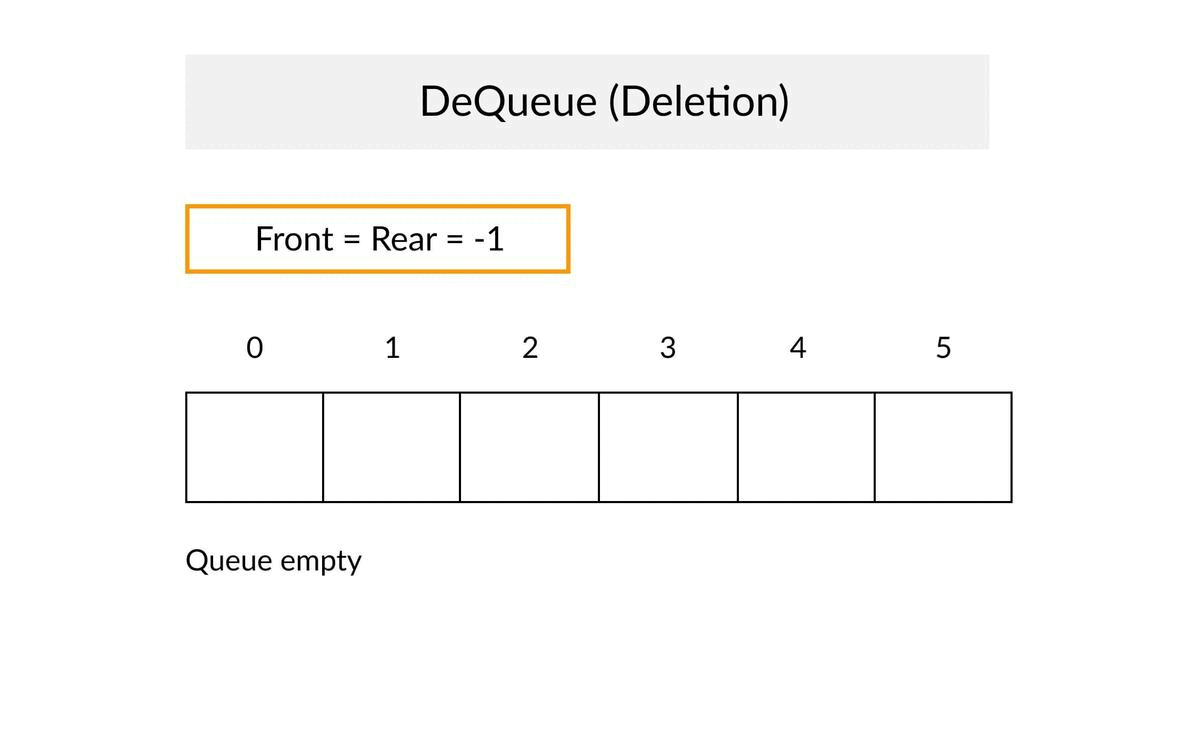
✔When an element is inserted in a queue, the concept is called EnQueue.
✔When an element is removed from the queue, the concept is called DeQueue.
✔DeQueueing an empty queue is called underflow (treat as Exception)
✔EnQueuing an element in a full queue is called overflow (treat as Exception).
Applications of Queue
✔Operating systems schedule jobs (with equal priority) in the order of arrival (e.g., a print queue).
✔Simulation of real-world queues such as lines at a ticket counter, or any other first come the first-served scenario requires a queue.
✔Multiprogramming. Asynchronous data transfer (file IO, pipes, sockets).
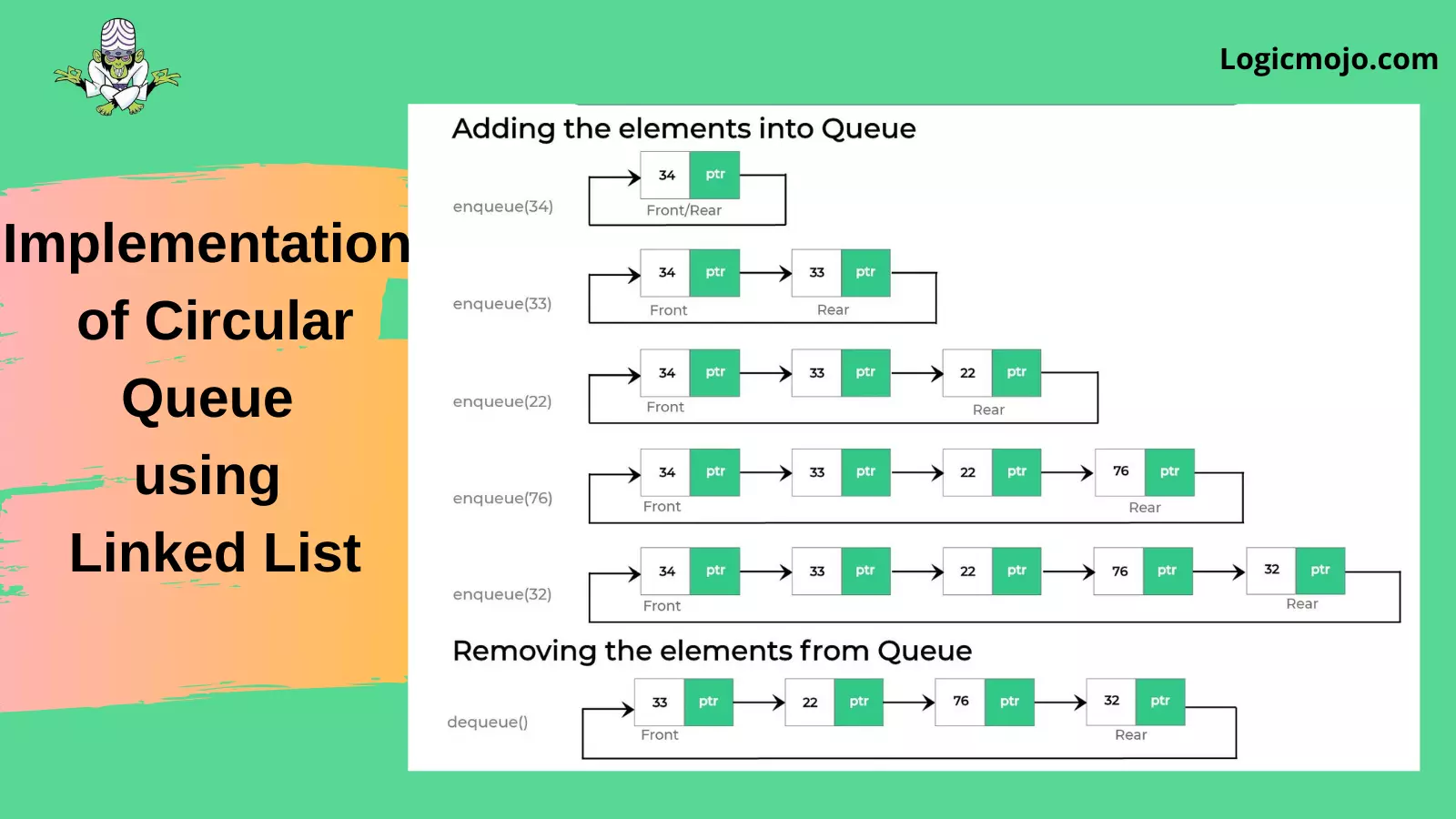
Implementation of Circular Queue using Linked List
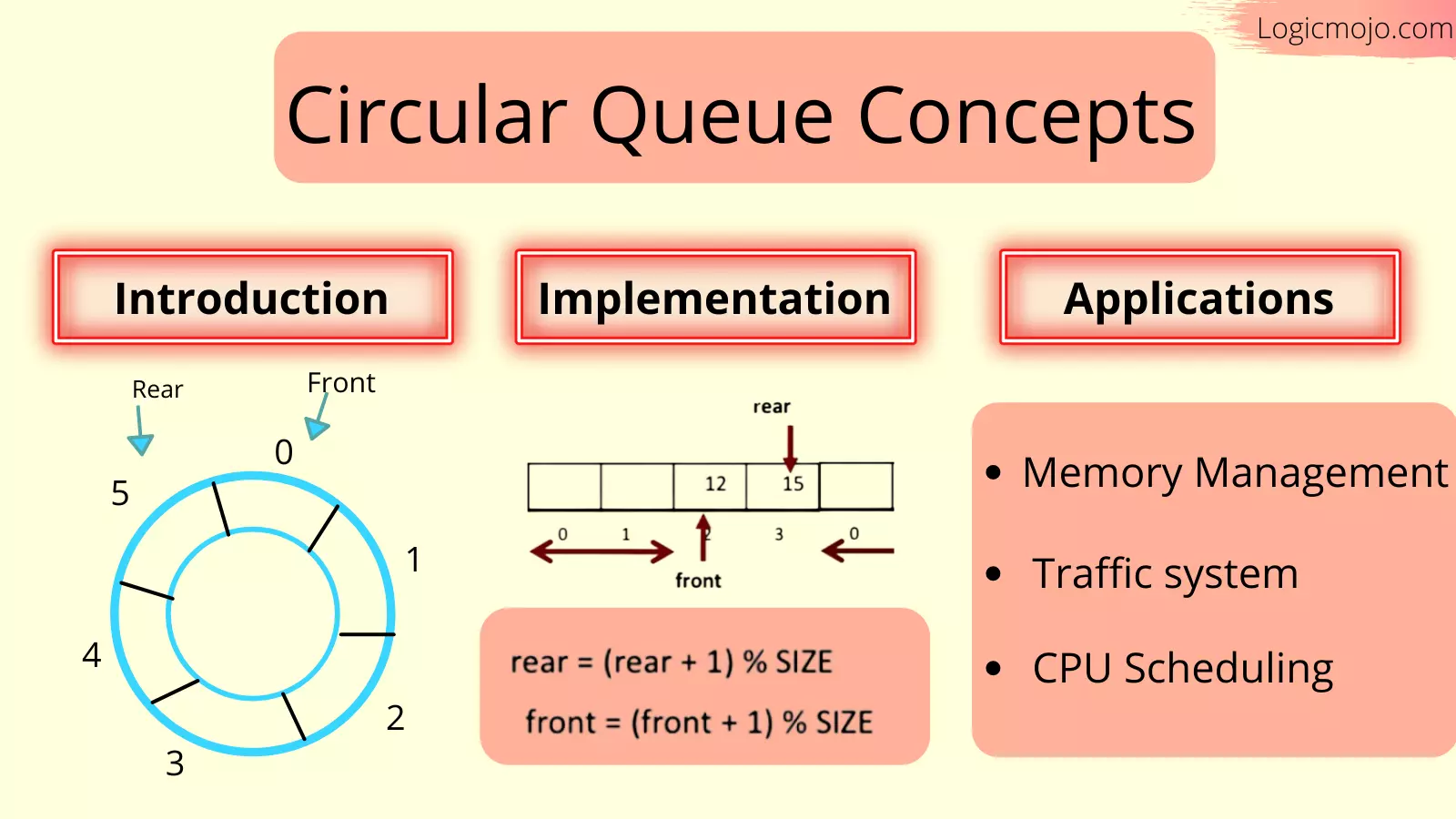
Operations on Circular Queue:
For enQueue
✔Create a new node dynamically and insert value into it
✔Check if front==NULL, if it is true then front = rear = (newly created node)
✔If it is false then rear=(newly created node) and rear node always contains the address of the front node.
For Dequeue
✔Check whether queue is empty or not means front == NULL.
✔If it is empty then display Queue is empty. If queue is not empty then step 3
✔Check if (front==rear) if it is true then set front = rear = NULL else move the front forward in queue, update address of front in rear node and return the element.
Below is the code implementation in Python
# Python3 program for insertion and
# deletion in Circular Queue
# Structure of a Node
class Node:
def __init__(self):
self.data = None
self.link = None
class Queue:
def __init__(self):
front = None
rear = None
# Function to create Circular queue
def enQueue(q, value):
temp = Node()
temp.data = value
if (q.front == None):
q.front = temp
else:
q.rear.link = temp
q.rear = temp
q.rear.link = q.front
# Function to delete element from
# Circular Queue
def deQueue(q):
if (q.front == None):
print("Queue is empty")
return -999999999999
# If this is the last node to be deleted
value = None # Value to be dequeued
if (q.front == q.rear):
value = q.front.data
q.front = None
q.rear = None
else: # There are more than one nodes
temp = q.front
value = temp.data
q.front = q.front.link
q.rear.link = q.front
return value
# Function displaying the elements
# of Circular Queue
def displayQueue(q):
temp = q.front
print("Elements in Queue are:end="")")
while (temp.link != q.front):
print(temp.data,end = " ")
temp = temp.link
print(temp.data)