Fibonacci Series In C

What Is Fibonacci Series in C?

Fibonacci Series in C: In the fibonacci series, the next number is the sum of the preceding two numbers, such as 0, 1, 1, 2, 3, 5, 8, 13, 21, and so on. The fibonacci series' first two integers are 0 and 1.

The Fibonacci Series Looks like this :

 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89.............                     

The following number is obtained by adding the two preceding numbers:

1. The 2 is obtained by adding the two digits preceding it (1+1).

2. The 3 is obtained by adding the two digits preceding it (1+2).

3. the 5 is (2+3),

4. and so forth!

Spiral Pattern in Fibonacci Series

The Fibonacci Series is composed of the numbers 0, 1, 1, 2, 3, 5, 8, 13, 21, and so on. It's challenging to tell what's so intriguing about this sequence just by looking at it. So, let us see why learning about the Fibonacci series is fascinating through a demonstration. Make various square shapes the width of these Fibonacci numbers and arrange them as shown in the picture below.

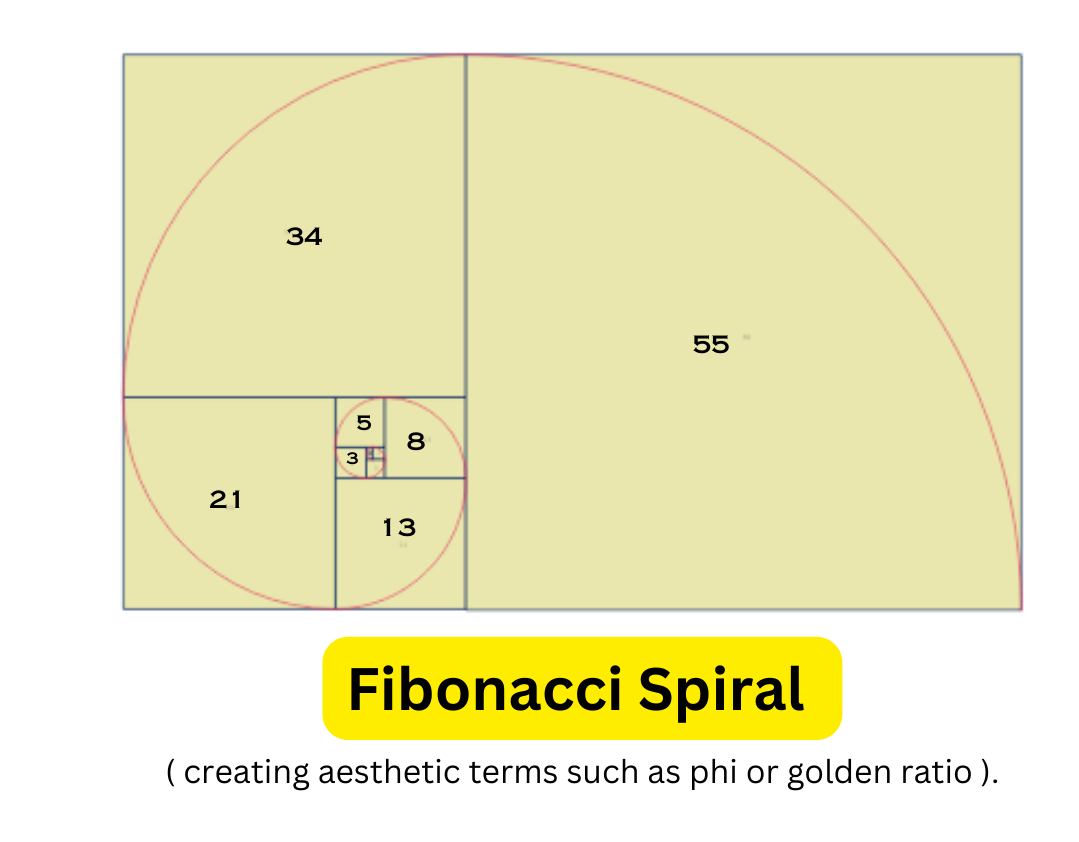
For example, consider this pattern of Fibonacci spiral in Shell.

The Fibonacci sequence has many interesting properties, but one in particular stands out: the ratio of any two consecutive numbers in the sequence is roughly the same as the ratio of the next two numbers.

For example, dividing 5 by 3 yields 1.666666666666667. When we split 13 by 8, we get 1.6. As you can see, as you progress down the sequence, the ratios get closer and closer to 1.6.

Fibonacci Series up to n terms

Let us now look at how to write a program that anticipates a Fibonacci series up to a certain number.

#include <stdio.h>
int main() {

  int i, n;

  // initialize first and second terms
  int term1 = 0, term2 = 1;

  // initialize the next term (3rd term)
  int nextTerm = term1 + term2;

  // get no. of terms from user
  printf("Number of terms is : ");
  scanf("%d", &n);

  // print the first two terms term1 and term2
  printf("The Fibonacci Series is : %d, %d, ", term1, term2);

  // print 3rd to nth terms
  for (i = 3; i <= n; ++i) {
    printf("%d, ", nextTerm);
    term1 = term2;
    term2 = nextTerm;
    nextTerm = term1 + term2;
  }

  return 0;
}
                     

Output

Number of terms is : 13
The Fibonacci Series is : 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,                      

Crack your next tech interview with confidence!

Fibonacci Series using Recursion

Recursive programming is a form of programming in which a function repeatedly calls itself. It is useful for breaking down complex issues into smaller and smaller sub-problems until they can be solved. As a result, recursive programming is a powerful problem-solving technique.

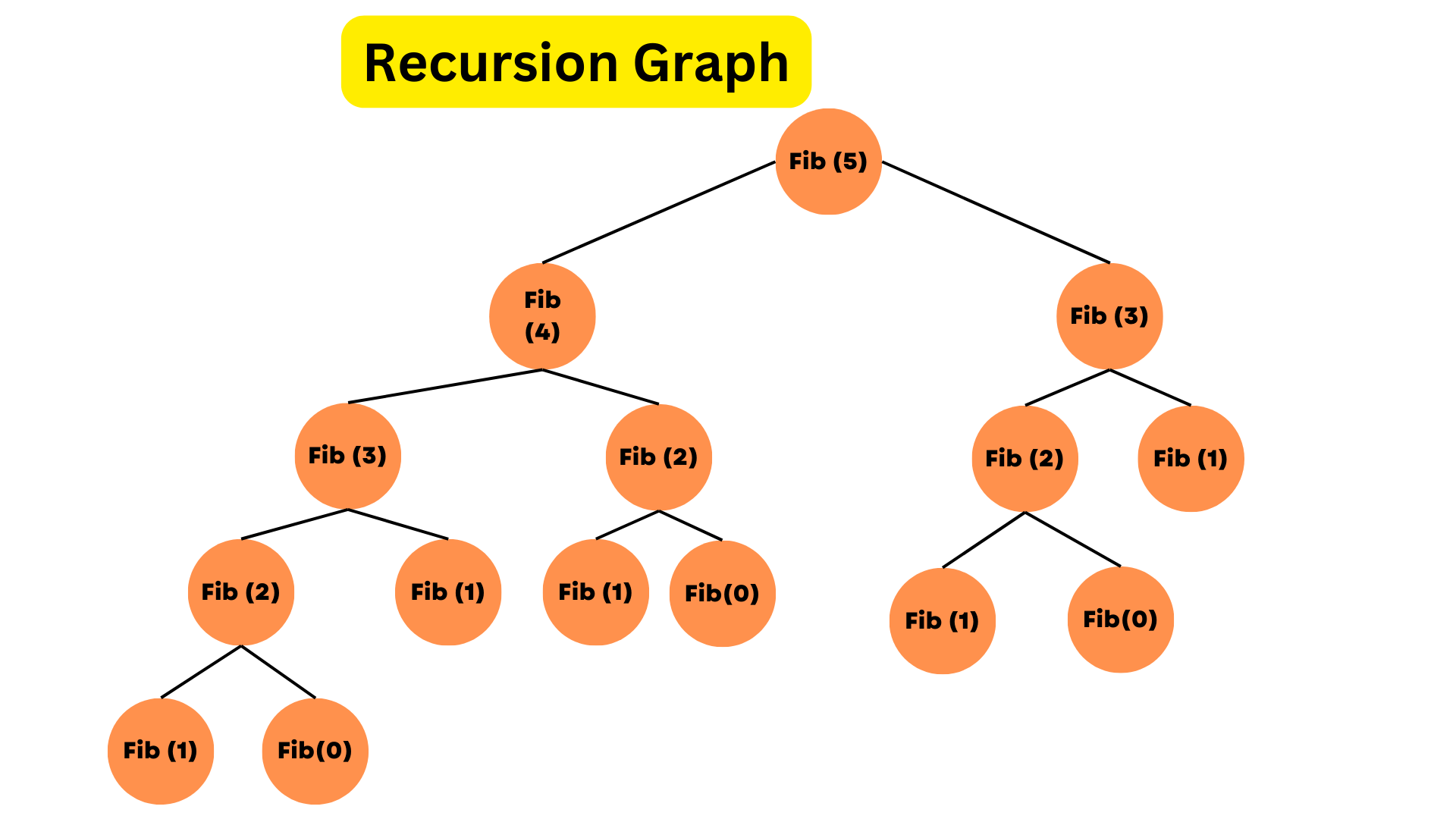
Let's look at a recursive fibonacci series program in C.

#include<stdio.h>

int FibS(int n){
    
    if(n <= 1)
        return n;
        
    return FibS(n-1) + FibS(n-2);
    
}

int main()
{
    int n = 10;

    for(int i = 0; i < n; i++)
        printf("Fibonacci Series is : %d, ",FibS(i));

    return 0;
}                 

Output

Fibonacci Series is : 0, Fibonacci Series is : 1, Fibonacci Series is : 1, Fibonacci Series is : 2, Fibonacci Series is : 3, 
Fibonacci Series is : 5, Fibonacci Series is : 8, Fibonacci Series is : 13, Fibonacci Series is : 21, 
Fibonacci Series is : 34, Fibonacci Series is : 55, Fibonacci Series is : 89, Fibonacci Series is : 144,                    

Fibonacci Sequence Up to a Certain Number

Let us now look at how to create a program that anticipates a Fibonacci series up to a certain number.

#include <stdio.h>
int main() {
  int term1 = 0, term2 = 1, nextTerm = 0, n;
  printf("Enter a positive number: ");
  scanf("%d", &n);

  // displays the first two terms which is always 0 and 1
  printf("Fibonacci Series: %d, %d, ", term1, term2);
  nextTerm = term1 + term2;

  while (nextTerm <= n) {
    printf("%d, ", nextTerm);
    term1 = term2;
    term2 = nextTerm;
    nextTerm = term1 + term2;
  }

  return 0;
}                       

Output

Enter a positive number: 500
Fibonacci Series: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377,                    

Fibonacci Series without recursion

Let's look at the fibonacci series program in c without recursion.

#include<stdio.h>    
int main()    
{    
 int num1=0,num2=1,num3,i,number;    
 printf("Enter the number of elements:");    
 scanf("%d",&number); 
 //printing 0 and 1 
 printf("\n%d %d",num1,num2);  
 //loop starts from 2 because 0 and 1 are already printed 
 for(i=2;i<number;++i)   
 {    
  num3=num1+num2;    
  printf(" %d,",num3);    
  num1=num2;    
  num2=num3;    
 }  
  return 0;  
 }                      

Output

Enter the number of elements:13

0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,                  

Fibonacci Series using Dynamic Programming

By storing the Fibonacci numbers determined thus far, we can avoid the repetitive work done in first method.

#include
 
int fibS(int num)
{
  /* Declare an array to store Fibonacci numbers. */
  int f[num+2];  
  int i;
 
  /* 0th and 1st number of the series are 0 and 1*/
  f[0] = 0;
  f[1] = 1;
 
  for (i = 2; i <= num; i++)
  {
      f[i] = f[i-1] + f[i-2];
  }
 
  return f[num];
}
 
int main ()
{
  int num = 13;
  printf("Number is : %d", fibS(num));
  getchar();
  return 0;
}                       

Output

Number is : 233                  

Applications

The Fibonacci sequence has many practical uses, particularly in finance. The Fibonacci sequence has been used in a variety of disciplines, including botany, music, and architecture. Fibonacci numbers are frequently used in botany to determine the number of petals on a flower. Fibonacci numbers can be used to generate rhythms and chord progressions in music. Fibonacci numbers can also be used in architecture to generate harmonic proportions in buildings.

Conclusions

You learned about the Fibonacci series and its mathematical interpretation in this Fibonacci Series in C, article. You also learned some fascinating details about the Fibonacci sequence, such as its presence in nature. Finally, we covered how the Fibonacci sequence is implemented using recursion.

Good luck and happy learning!