 Logicmojo - Updated Dec 12, 2023
Logicmojo - Updated Dec 12, 2023
Most of the algorithms that we’ve been dealing with have been pretty slow, and seem inefficient. However, they tend to come up a lot in computer science courses and theoretical explanations because they are often used as the naive approach, or the simplest implementation of sorting a collection.
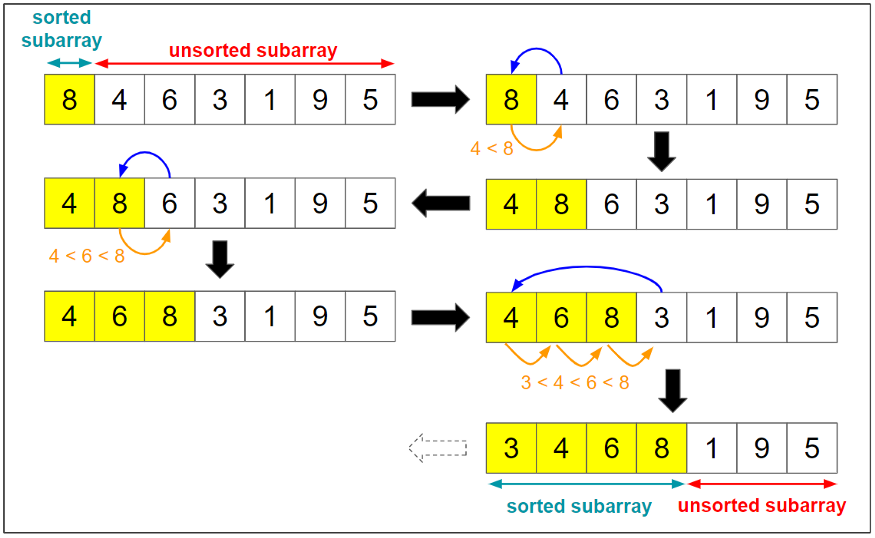
Insertion sort is a simple sorting algorithm that works similar to the way you sort playing cards in your hands. The array is virtually split into a sorted and an unsorted part. Values from the unsorted part are picked and placed at the correct position in the sorted part.
Insertion Algorithms: Steps on how it works:
1. If it is the first element, it is already sorted.
2. Pick the next element.
3. Compare with all the elements in sorted sub-list.
4. Shift all the the elements in sorted sub-list that is greater than the value to be sorted.
5. Insert the value.
6. Repeat until list is sorted.
Below is an array of 4 numbers, which need to be sorted. We will use Insertion Sort Algorithm, to sort this array:
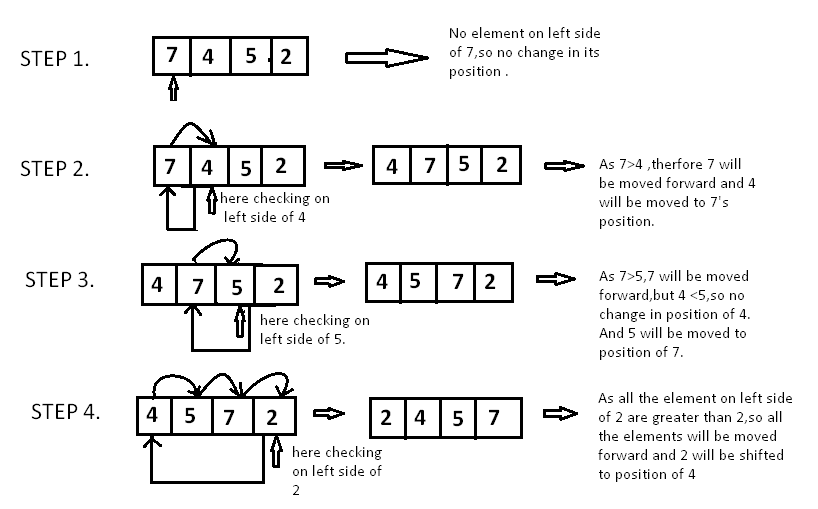
Since 7 is the first element and has no other element to be compared with, it remains at its position. Now when on moving towards 4, 7 is the largest element in the sorted list and greater than 4. So, move 4 to its correct position, which is before 7. Similarly with 5, as 7 (largest element in the sorted list) is greater than 5, move 5 to its correct position. Finally for 2, all the elements on the left side of 2 (sorted list) are moved one position forward as all are greater than 2 and then 2 is placed in the first position. Finally, the given array will result in a sorted array.
Algorithm
insertionSort(array)
mark first element as sorted
for each unsorted element X
'extract' the element X
for j < - lastSortedIndex down to 0
if current element j > X
move sorted element to the right by 1
break loop and insert X here
end insertionSort
Characteristics of Insertion Sort
1. It is efficient for smaller data sets, but very inefficient for larger lists.
2. Insertion Sort is adaptive, that means it reduces its total number of steps if given a partially sorted list, hence it increases its efficiency.
3. Its space complexity is less. Insertion sort requires a single additional memory space.
4. Overall time complexity of Insertion sort is O(n2).
Implementation in Python
# Insertion sort in Python def insertionSort(array): for step in range(1, len(array)): key = array[step] j = step - 1 # Compare key with each element on the left of it until an element smaller than it is found # For descending order, change key<array[j] to key>array[j]. while j >= 0 and key < array[j]: array[j + 1] = array[j] j = j - 1 # Place key at after the element just smaller than it. array[j + 1] = key data = [9, 5, 1, 4, 3] insertionSort(data) print('Sorted Array in Ascending Order:') print(data)
Implementation in C++
// Insertion sort in C++ #include <iostream> using namespace std; // Function to print an array void printArray(int array[], int size) { for (int i = 0; i < size; i++) { cout << array[i] << " "; } cout << endl; } void insertionSort(int array[], int size) { for (int step = 1; step < size; step++) { int key = array[step]; int j = step - 1; // Compare key with each element on the left of it until an element smaller than // it is found. // For descending order, change key<array[j] to key>array[j]. while (key < array[j] && j >= 0) { array[j + 1] = array[j]; --j; } array[j + 1] = key; } } // Driver code int main() { int data[] = {9, 5, 1, 4, 3}; int size = sizeof(data) / sizeof(data[0]); insertionSort(data, size); cout << "Sorted array in ascending order:\n"; printArray(data, size); }
Time & Space Complexity Analysis
Worst Case Complexity: O(n2)
Suppose, an array is in ascending order, and you want to sort it in descending order. In this case, worst case complexity occurs.
Hence, the time complexity is O(n2).
Best Case Complexity: O(n)
When the array is already sorted, the outer loop runs for n number of times whereas the inner loop does not run at all. So, there are only n number of comparisons. Thus, complexity is linear.
Average Case Complexity: O(n2)
It occurs when the elements of an array are in jumbled order (neither ascending nor descending).
Space Complexity of Insertion sort
Space complexity is O(1) because an extra variable key is used
With this article at Logicmojo, you must have the complete idea of analyzing Insertion Sort algorithm.
Good Luck & Happy Learning!!
Frequently Asked Questions (FAQs)
Insertion sort is a simple sorting algorithm that works similar to the way you sort playing cards in your hands. This method is efficient for smaller lists, and it can also be advantageous when the input is 'almost' sorted.
Let's take an example:
We will sort the following list in ascending order: [8, 3, 6, 4, 5]
- Start from the second element: here it's 3. Since 3 is less than 8, we move 8 one place to the right and insert 3 in the first position. The list becomes [3, 8, 6, 4, 5].
- Move to the next element: 6. 6 is less than 8 but more than 3, so we move 8 to the right and insert 6 before 8. The list becomes [3, 6, 8, 4, 5].
- The next element is 4. 4 is less than 8, 6 and more than 3, so we move 8 and 6 to the right and insert 4 before 6. The list becomes [3, 4, 6, 8, 5].
- The final element is 5. 5 is less than 8 but more than 4, so we move 8 to the right and insert 5 before 8. The list becomes [3, 4, 5, 6, 8].
We have now finished sorting the entire list.
In the worst case scenario, the time complexity of insertion sort is O(n^2) where n is the number of elements in the list. This happens when the list is sorted in reverse order, because each insertion is as far back as possible.
While not efficient for large data sets, the insertion sort has uses in certain situations. For instance, it has a best case time complexity of O(n) when the input list is already sorted, it performs well on nearly sorted lists, it's easy to implement, and it's efficient on small data sets.
Insertion sort is a simple sorting algorithm that works by iteratively building a sorted portion of an array. It starts by considering the first element of the array as the sorted portion, as an array with a single element can be considered already sorted. Then, it compares the second element to the elements in the sorted portion and inserts it in the correct position.
Here's a step-by-step explanation of how insertion sort works:
1. Starting with the second element (index 1) of the array, compare it to the elements in the sorted portion (elements before the current position).
2. If the second element is smaller than any element in the sorted portion, shift the elements in the sorted portion to the right to create space for inserting the second element.
3. Continue comparing the second element to the elements in the sorted portion until either the beginning of the array is reached, or an element in the sorted portion is smaller than or equal to the second element.
4. Insert the second element into its correct position in the sorted portion.
5. Move to the next element (index 2) of the array and repeat steps 2 to 4, comparing it to the elements in the sorted portion and inserting it into the correct position.
6. Repeat steps 2 to 5 for all remaining elements in the array until the entire array is sorted.
To better understand the process, let's walk through an example. Consider the following array: [5, 2, 4, 6, 1, 3].
1. Initially, the first element (5) is considered as the sorted portion.
2. The second element (2) is smaller than 5, so we shift 5 to the right to make space for 2. The array becomes [2, 5, 4, 6, 1, 3].
3. The third element (4) is smaller than 5, so we shift 5 to the right and insert 4 into the correct position in the sorted portion. The array becomes [2, 4, 5, 6, 1, 3].
4. The fourth element (6) is greater than all elements in the sorted portion, so we leave it in its position.
5. The fifth element (1) is smaller than 6, so we shift 6 to the right and insert 1 into the correct position. The array becomes [2, 4, 5, 1, 6, 3].
6. The sixth element (3) is smaller than 6, so we shift 6 to the right, shift 5 to the right, and insert 3 into the correct position. The final sorted array is [1, 2, 3, 4, 5, 6].
The process continues until all elements are sorted, with each iteration expanding the sorted portion of the array. Insertion sort has a time complexity of O(n^2) in the worst and average case, where n is the number of elements in the array. However, it has a best-case time complexity of O(n) when the array is already sorted, making it efficient for small arrays or partially sorted arrays.
This is an example of the insertion sort algorithm implemented in C:
#include <stdio.h>
void insertionSort(int arr[], int n) {
int i, j, key;
for (i = 1; i < n; i++) {
key = arr[i];
j = i - 1;
/* Compare key with elements of the sorted portion and shift them to the right if they are greater than key */
while (j >= 0 && arr[j] > key) {
arr[j + 1] = arr[j];
j = j - 1;
}
arr[j + 1] = key; // Insert the key into its correct position in the sorted portion
}
}
int main() {
int arr[] = {5, 2, 4, 6, 1, 3};
int n = sizeof(arr) / sizeof(arr[0]);
insertionSort(arr, n);
printf("Sorted array: ");
for (int i = 0; i < n; i++) {
printf("%d ", arr[i]);
}
return 0;
}
Let's break down the code step by step:
1. The `insertionSort` function takes an array `arr[]` and the size of the array `n` as parameters.
2. Inside the `insertionSort` function, we define three variables: `i` for the outer loop, `j` for the inner loop, and `key` to temporarily store the value being inserted into the sorted portion.
3. The outer loop starts from the second element (index 1) and iterates until the last element (index `n-1`).
4. Inside the outer loop, we assign the value of the current element (arr[i]) to the `key` variable.
5. We initialize `j with the index preceding the current element (i.e., `i-1`).
6. The inner loop compares the `key` with the elements in the sorted portion (from `j` to 0) and shifts the greater elements to the right, creating space for inserting the `key`.
7. The inner loop continues until it reaches the beginning of the array or an element in the sorted portion that is smaller than or equal to the `key`.
8. After the inner loop, we insert the `key` into its correct position by assigning it to `arr[j + 1]`.
9. The outer loop continues until all elements have been processed and inserted into the sorted portion.
10. In the `main` function, we declare an array `arr[]` and initialize it with values.
11. We calculate the size of the array `n` by dividing the total size of the array by the size of a single element.
12. We call the `insertionSort` function, passing the array and its size.
13. Finally, we print the sorted array using a loop and return 0 to indicate successful execution of the program.
When you run this code, it will sort the array using the insertion sort algorithm and display the sorted array as output. In the provided example, the output would be:
"Sorted array: 1 2 3 4 5 6".
The time complexity of insertion sort is O(n^2) in the worst and average case, where n is the number of elements in the array. This means that the time it takes to execute the algorithm grows quadratically with the size of the input array.
To understand why the time complexity is O(n^2), let's analyze the steps involved in insertion sort. In the worst case, each element needs to be compared and possibly shifted multiple times to its correct position in the sorted portion. The outer loop iterates n-1 times, as we start comparing from the second element. In the worst case, the inner loop iterates i times for each iteration of the outer loop, where i is the current index of the outer loop. Thus, the total number of comparisons and shifts can be approximated by the sum of 1 + 2 + 3 + ... + (n-1), which is equal to (n-1)(n-2)/2. In Big O notation, this simplifies to O(n^2).
However, it's worth noting that insertion sort has a best-case time complexity of O(n) when the array is already sorted. In the best case scenario, each element is already in its correct position in the sorted portion, and there is no need for any shifts. The algorithm simply performs n-1 comparisons in the outer loop, resulting in linear time complexity.
Regarding the space complexity, insertion sort has a space complexity of O(1) since it sorts the elements in-place, without requiring any additional memory that grows with the size of the input array. The algorithm only uses a constant amount of memory for storing variables such as indices and temporary values, regardless of the array size.
In summary, insertion sort has a time complexity of O(n^2) in the worst and average case, and O(n) in the best case. Its space complexity is O(1). Insertion sort is efficient for small arrays or partially sorted arrays, but it becomes less efficient as the array size grows larger.
Insertion sort, despite its relatively simple implementation and higher time complexity compared to more advanced sorting algorithms like quicksort or mergesort, still has its use cases and advantages in certain scenarios. Here are some reasons why insertion sort is used:
1. Simplicity: Insertion sort has a straightforward implementation with a small and easy-to-understand codebase. It is a good algorithm to use when simplicity and clarity of code are desired, especially for educational purposes or when working with small input sizes.
2. Efficiency for Small Arrays: Insertion sort performs well on small arrays or partially sorted arrays. For small input sizes, the quadratic time complexity of insertion sort does not have a significant impact on performance. In fact, insertion sort has a linear time complexity of O(n) in the best case scenario when the array is already sorted.
3. Partially Sorted Arrays: If an array is already partially sorted or has elements that are in close proximity to their final sorted positions, insertion sort can be more efficient compared to other sorting algorithms. It takes advantage of the existing order and minimizes the number of comparisons and shifts needed to sort the array.
4. Online Sorting: Insertion sort is an "online" algorithm, meaning it can sort data as it receives it or on-the-fly without needing to have all the data in advance. This property makes it useful in situations where new elements are continuously added to an already sorted list.
5. Adaptive: Insertion sort is an adaptive algorithm, meaning it performs better on partially sorted arrays. When the input array is already partially sorted, insertion sort requires fewer comparisons and shifts, resulting in improved performance compared to other algorithms.
6. In-Place Sorting: Insertion sort operates in-place, meaning it doesn't require additional memory proportional to the size of the input array. It is useful when memory resources are limited or when minimizing memory usage is a requirement.
7. Stable Sorting: Insertion sort is a stable sorting algorithm, meaning it preserves the relative order of equal elements. This can be important when sorting objects with multiple keys or sorting data that has associated metadata or attributes.
While insertion sort may not be the most efficient sorting algorithm for large or completely unsorted arrays, it still offers advantages in terms of simplicity, adaptability, and efficiency for certain scenarios. Understanding the characteristics and trade-offs of different sorting algorithms helps in selecting the most appropriate one for a specific use case.
Quicksort and insertion sort are two different sorting algorithms with distinct characteristics and performance trade-offs. Here's a detailed comparison of the two:
1. Algorithm Approach:
- Quicksort: Quicksort is a divide-and-conquer algorithm that recursively partitions the input array into smaller subarrays and sorts them independently. It selects a pivot element, partitions the array around the pivot, and then recursively applies the same process to the subarrays on either side of the pivot.
- Insertion Sort: Insertion sort, on the other hand, is an incremental sorting algorithm that builds the sorted portion of the array one element at a time. It iteratively selects an element and inserts it into its correct position in the sorted portion, shifting elements if necessary.
2. Time Complexity:
- Quicksort: Quicksort has an average-case time complexity of O(n log n) and a worst-case time complexity of O(n^2). However, in practice, it often outperforms other sorting algorithms due to its efficient partitioning scheme and average-case behavior.
- Insertion Sort: Insertion sort has an average and worst-case time complexity of O(n^2). It requires shifting elements in the sorted portion for every comparison, leading to a quadratic time complexity. However, its best-case time complexity is O(n) when the array is already sorted.
3. Performance:
- Quicksort: Quicksort is generally faster than insertion sort for large input sizes and random or unsorted arrays. It has better average-case performance due to its ability to quickly partition the array and sort subarrays independently. However, its worst-case time complexity can degrade the performance significantly.
- Insertion Sort: Insertion sort performs well on small input sizes, partially sorted arrays, and nearly sorted arrays. It is efficient when the array is already partially sorted because it minimizes the number of comparisons and shifts. However, its performance degrades quickly as the array size grows larger.
4. Space Complexity:
- Quicksort: Quicksort typically has a space complexity of O(log n) for the recursive call stack. In the worst case, it may require O(n) additional space for partitioning. However, in practice, it usually requires less additional memory due to in-place partitioning.
- Insertion Sort: Insertion sort has a space complexity of O(1) since it operates in-place and doesn't require additional memory proportional to the input size.
5. Stability:
- Quicksort: Quicksort is not a stable sorting algorithm. Equal elements may change their relative order during the partitioning process.
- Insertion Sort: Insertion sort is a stable sorting algorithm. It preserves the relative order of equal elements during the insertion process.
In summary, Quicksort is generally preferred for larger input sizes and random or unsorted arrays due to its average-case efficiency, while insertion sort is suitable for small arrays, partially sorted arrays, or cases where simplicity and adaptability are desired. The choice between the two algorithms depends on the specific requirements, characteristics of the input data, and desired trade-offs between time complexity and stability.
Yes, insertion sort is a stable sorting algorithm.
A sorting algorithm is considered stable if it maintains the relative order of elements with equal keys. In other words, if there are two elements in the original array that have the same key, and one comes before the other, a stable sorting algorithm will ensure that the element that appeared earlier in the input array will also appear earlier in the sorted array.
In the case of insertion sort, when comparing an element to the elements in the sorted portion and finding its correct position, if there are equal elements, the algorithm performs the insertion such that the element being inserted is placed after the equal elements. This ensures that the relative order of equal elements is preserved.
Let's consider an example to illustrate the stability of insertion sort. Suppose we have an array with elements and their corresponding indices as follows:
[5(1), 2(2), 4(3), 6(4), 1(5), 3(6)]
In this example, the numbers in parentheses represent the original indices of the elements in the input array. Now, let's apply insertion sort to this array.
During the sorting process, when we compare the second element (2) with the first element (5) in the sorted portion, we find that 2 is smaller and needs to be inserted before 5. Since 5 and 2 have the same key, the algorithm will place the second element (2) before the first element (5) in the sorted portion, preserving their original relative order.
The sorted array after applying insertion sort will be:
[1(5), 2(2), 3(6), 4(3), 5(1), 6(4)]
As you can see, the relative order of equal elements (5 and 2) in the input array is preserved in the sorted array. This demonstrates that insertion sort is a stable sorting algorithm.
The stability of insertion sort makes it useful in scenarios where maintaining the original order of elements with equal keys is important, such as when sorting objects with multiple attributes or when working with data that has associated metadata.Determining the "best" sorting algorithm depends on various factors such as the characteristics of the input data, the desired performance, the available resources, and the specific requirements of the application. There is no one-size-fits-all answer to which sorting algorithm is universally the best. Instead, different algorithms have different strengths and weaknesses. Here's an overview of some popular sorting algorithms and their considerations:
1. Quicksort: Quicksort is often considered one of the best general-purpose sorting algorithms. It has an average-case time complexity of O(n log n), making it highly efficient for large input sizes and random or unsorted data. However, its worst-case time complexity of O(n^2) can be a concern in some scenarios.
2. Mergesort: Mergesort is a stable sorting algorithm with a guaranteed worst-case time complexity of O(n log n). It is efficient for large input sizes and provides consistent performance across different data distributions. However, it requires additional memory proportional to the input size, which may be a limitation in memory-constrained environments.
3. Heapsort: Heapsort is an in-place sorting algorithm with a worst-case time complexity of O(n log n). It has a relatively small constant factor and can be efficient for large input sizes. However, it is not stable, meaning the original order of equal elements may not be preserved.
4. Insertion Sort: Insertion sort is simple and efficient for small input sizes, partially sorted arrays, or nearly sorted data. It has a best-case time complexity of O(n) when the array is already sorted. However, its worst-case time complexity of O(n^2) limits its scalability for larger input sizes.
5. Selection Sort: Selection sort is easy to understand and implement. It has a time complexity of O(n^2), making it inefficient for large input sizes. It is primarily used for educational purposes or when simplicity is prioritized over performance.
6. Radix Sort: Radix sort is a non-comparative sorting algorithm that works by distributing elements into buckets based on their digits or characters. It has a linear time complexity of O(kn), where k is the average number of digits or characters in the input. Radix sort is efficient for sorting integers or strings with fixed-length keys, but it requires additional memory and may not be suitable for all data types.
7. Timsort: Timsort is a hybrid sorting algorithm derived from merge sort and insertion sort. It is designed to perform well on a variety of real-world data. Timsort is stable, has a worst-case time complexity of O(n log n), and exhibits good performance on partially sorted or small input sizes. It is the default sorting algorithm in Python's standard library.
The best sorting algorithm depends on the specific requirements of your application. Consider factors such as the expected size of the input data, the data distribution, stability requirements, memory constraints, and desired trade-offs between time complexity and space complexity. It is often beneficial to benchmark and profile different algorithms with representative input data to determine the most suitable choice for a given situation.
The fastest sorting algorithm depends on various factors, including the characteristics of the input data and the specific requirements of the application. No single sorting algorithm is universally the fastest in all scenarios. However, some algorithms are known for their efficient average-case performance or specialized optimizations. Here are a few sorting algorithms known for their speed in certain situations:
1. Quicksort: Quicksort is often considered one of the fastest general-purpose sorting algorithms. It has an average-case time complexity of O(n log n), making it highly efficient for large input sizes and random or unsorted data. Quicksort's efficiency is attributed to its efficient partitioning scheme, which allows for the sorting of subarrays independently. However, in the worst case, its time complexity can degrade to O(n^2).
2. Mergesort: Mergesort is another efficient sorting algorithm with a worst-case time complexity of O(n log n). It is a divide-and-conquer algorithm that splits the input into smaller subarrays, sorts them, and then merges them back together. Mergesort is known for its consistent performance across different data distributions and its stability.
3. Radix Sort:Radix sort is a non-comparative sorting algorithm that operates on digits or characters. It has a linear time complexity of O(kn), where k is the average number of digits or characters in the input. Radix sort can be extremely fast for sorting integers or strings with fixed-length keys. It works by distributing elements into buckets based on each digit or character position, providing an efficient sorting mechanism for specific data types.
4. Counting Sort: Counting sort is an integer sorting algorithm that works well when the range of input values is known and relatively small. It counts the occurrences of each element and uses this information to place elements into their correct positions. Counting sort has a linear time complexity of O(n + k), where n is the number of elements and k is the range of values. It can be extremely fast for sorting small integers or objects with integer keys.
It's important to note that the "fastest" sorting algorithm can vary depending on the specific requirements and constraints of the application. Factors such as the input size, data distribution, stability requirements, memory constraints, and desired trade-offs between time complexity and space complexity all play a role in determining the most suitable sorting algorithm for a given scenario. It is often beneficial to evaluate and benchmark different algorithms using representative input data to choose the most efficient option for a particular use case.
Insertion sort, despite its simplicity and higher time complexity compared to more advanced sorting algorithms, offers several advantages in certain scenarios. Here are the advantages of insertion sort:
1. Simplicity: Insertion sort has a straightforward implementation and is relatively easy to understand and implement. It has a small and easy-to-understand codebase, making it a good choice for educational purposes, learning algorithms, or when simplicity and clarity of code are desired.
2. Efficiency for Small Arrays: Insertion sort performs well on small input sizes. For small arrays, the quadratic time complexity of insertion sort does not have a significant impact on performance. In fact, insertion sort has a linear time complexity of O(n) in the best case scenario when the array is already sorted. Therefore, it is efficient and can outperform more complex algorithms for small input sizes.
3. Partially Sorted Arrays: Insertion sort is efficient when the input array is already partially sorted or has elements that are in close proximity to their final sorted positions. It takes advantage of the existing order and minimizes the number of comparisons and shifts needed to sort the array. In such cases, insertion sort can perform significantly better than other sorting algorithms.
4. Online Sorting: Insertion sort is an "online" algorithm, meaning it can sort data as it is received or on-the-fly without needing to have all the data in advance. It works well when new elements are continuously added to an already sorted list. Insertion sort allows for incremental sorting, making it useful in scenarios where data is continuously updated or when sorting is required during ongoing operations.
5. Adaptive: Insertion sort is an adaptive algorithm. It performs better on partially sorted arrays because it minimizes the number of comparisons and shifts. As the sorted portion grows, the algorithm requires fewer comparisons and shifts to place new elements in their correct positions, leading to improved performance compared to algorithms that do not take advantage of existing order.
6. In-Place Sorting: Insertion sort operates in-place, meaning it sorts the elements directly within the input array without requiring additional memory that grows with the size of the input. It only uses a constant amount of memory for storing variables such as indices and temporary values, making it memory-efficient. This is particularly useful when memory resources are limited or minimizing memory usage is a requirement.
7. Stability: Insertion sort is a stable sorting algorithm, meaning it preserves the relative order of equal elements during the sorting process. If there are multiple elements with the same key, the order of these elements is maintained, which is important in certain applications that rely on the preservation of original order or when sorting objects with multiple attributes.
In summary, insertion sort offers advantages in terms of simplicity, efficiency for small arrays and partially sorted arrays, adaptability to existing order, online sorting capabilities, in-place sorting with minimal memory requirements, and stability. Understanding the strengths and weaknesses of insertion sort helps in selecting the most appropriate algorithm for specific use cases and considering the trade-offs between performance and complexity.
While insertion sort has its advantages in certain scenarios, it also has limitations that make it less suitable for other situations. Here are the limitations of insertion sort:
1. Quadratic Time Complexity: Insertion sort has a quadratic time complexity of O(n^2) in the worst and average case. This means that the time it takes to execute the algorithm grows quadratically with the size of the input array. For large input sizes, insertion sort can become inefficient compared to more advanced sorting algorithms with better time complexities, such as quicksort or mergesort.
2. Lack of Scalability: Due to its quadratic time complexity, insertion sort is not scalable for large input sizes. As the array size increases, the number of comparisons and shifts required also grows exponentially. Consequently, insertion sort becomes increasingly slow and impractical compared to algorithms with better scalability.
3. Inefficient for Randomly Ordered Arrays: Insertion sort is not efficient for sorting randomly ordered arrays. Since it compares and shifts elements individually, it requires many comparisons and shifts to place elements in their correct positions. This leads to significant overhead, resulting in a suboptimal performance compared to algorithms that utilize more efficient partitioning and merging strategies.
4. Limited Use for Repeated Elements: Insertion sort does not efficiently handle arrays with a large number of repeated elements. When there are many repeated elements, insertion sort still performs comparisons and shifts even if the elements are already in their correct positions within the sorted portion. This inefficiency contributes to the overall slowness of insertion sort in these cases.
5. Not Suitable for Parallelization: Insertion sort does not lend itself well to parallelization or parallel computing. Its nature of sorting elements individually and sequentially makes it difficult to efficiently distribute the work among multiple processing units. This limits its performance on systems that can leverage parallel computing power.
6. Memory Usage: While insertion sort operates in-place and does not require additional memory proportional to the input size, it still needs a small amount of auxiliary memory for variables and temporary values. In scenarios with severely limited memory resources, this additional memory usage can be a constraint.
In summary, the limitations of insertion sort primarily stem from its quadratic time complexity, which makes it less efficient for large input sizes and randomly ordered arrays. Its inefficiency with repeated elements, lack of scalability, limited parallelization potential, and modest memory usage can further restrict its suitability for certain use cases.
Understanding these limitations helps in selecting the most appropriate sorting algorithm for specific scenarios, considering factors such as input size, data distribution, and performance requirements.
Insertion sort is most effective and recommended in the following scenarios:
1. Small Input Sizes: Insertion sort is well-suited for sorting small input sizes. Its quadratic time complexity becomes less of a concern when dealing with a limited number of elements. For small arrays, the simplicity and ease of implementation of insertion sort can outweigh its slightly slower performance compared to more complex sorting algorithms.
2. Partially Sorted Arrays: When the input array is already partially sorted or has elements that are in close proximity to their final sorted positions, insertion sort can be highly efficient. It takes advantage of the existing order and minimizes the number of comparisons and shifts required to sort the array. In such cases, insertion sort can outperform other sorting algorithms that do not consider the initial order.
3. Nearly Sorted Arrays: If the input array is almost sorted, meaning that only a few elements are out of order, insertion sort can be an excellent choice. It has an adaptive nature and performs well when the array is already close to being sorted. In such scenarios, insertion sort requires fewer comparisons and shifts, making it an efficient sorting option.
4. Online Sorting: Insertion sort is suitable for situations where new elements are continuously added to an already sorted list or when data is received incrementally. It can be used in real-time applications where sorting needs to be performed as data arrives. Since insertion sort can incrementally build the sorted portion of the array, it accommodates online sorting requirements.
5. Stable Sorting: If maintaining the original order of equal elements is crucial, insertion sort is a preferred choice. It is a stable sorting algorithm, meaning it preserves the relative order of equal elements. This characteristic is essential in applications that rely on the original order or when sorting objects with multiple attributes.
6. Simple Implementations: Insertion sort is an elementary sorting algorithm with a simple implementation. It is easy to understand and implement, making it suitable for educational purposes, learning algorithms, or as a starting point for more complex sorting algorithms. It serves as a stepping stone to grasp fundamental sorting concepts before exploring more sophisticated techniques.
In summary, insertion sort is ideal for small input sizes, partially sorted or nearly sorted arrays, online sorting scenarios, stable sorting requirements, and situations where simplicity and ease of implementation are prioritized. Understanding the strengths and limitations of insertion sort helps in selecting the most appropriate algorithm for specific use cases, considering factors such as input size, data distribution, and performance requirements.
