Introduction

There are numerous methods for sorting. The subarray at the beginning of the array is sorted as selection sort executes, but the subarray at the end is not. The unsorted subarray is scanned for the next element to include in the sorted subarray by selection sort.

The following article will go over the Insertion Sort Algorithm. The insertion sort process is also straightforward. This article will be very useful and interesting to students who may encounter insertion sort as a topic in their exams. As a result, it has to be important to address the topic.

Insertion Sort

Insertion sort is an easy-to-understand algorithm for sorting that works in the same way that you would arrange playing cards in your hands. The array is divided into two parts: ordered and unsorted. Values from the unsorted part are selected and assigned to the appropriate location in the sorted part.

It iterates through the input components, expanding the sorted array with each iteration. It compares the present element to the element with the highest value in the sorted array. If the current element is greater, it leaves it in place and moves on to the next element; otherwise, it determines its proper position in the sorted array and moves it there. This is accomplished by moving all of the elements in the sorted array that are bigger than the current element one place ahead.

This picture will make you understand how insertion sort works, for sorting the values in an array:-

Here's another method to consider sorting. Assume you're playing a card game. You have the cards in your palm, and they are sorted. The dealer deals you one fresh card. You must position it correctly so that the cards you are holding remain sorted. In selection sort, each element added to the sorted subarray must be no smaller than the elements already there. However, in our card example, the new card may be smaller than some of the cards you already have, so you proceed down the line, comparing the new card to each card in your hand, until you find a spot for it.

You put the new card in its proper place, and your hand once again contains fully sorted cards. The dealer then deals you another card, and you continue the process. Then another card, and another, and so on, until the dealer ceases dealing cards to you.

Characteristics of Insertion Sort

1. This algorithm is one of the most basic, with an easy application.

2. Insertion sort is most effective for small data quantities.

3. Insertion sort is adaptive in nature, which means it is suitable for partially sorted data sets.

Insertion Sort Algorithm

Now, let's have a look at the pseudocode and Algorithm of the Insertion Sort

Pseudocode for Insertion Sort

procedure insertionSort(A: list of sortable items)
   n = length(A)
   for i = 1 to n - 1 do
       j = i
       while j > 0 and A[j-1] > A[j] do
           swap(A[j], A[j-1])
           j = j - 1
       end while
   end for
end procedure                  

Explanation

This algorithm sorts an array of items by repeatedly inserting an element from the unsorted part of the array into its proper position in the sorted portion of the array.

1. The procedure only accepts one argument, 'A,' which is a list of sortable objects. The length of the array A is given to the variable 'n'.

2. The outer for loop begins at index '1' and loops for 'n-1' cycles, where 'n' is the array's length.

3. The inner while loop begins at the outer for loop's current number i and compares each element to its left neighbor. The components are swapped if one element is smaller than its left neighbour.

4. The inner while loop moves an element to the left until it is lesser than the element to its left.

5. When the inner while loop is completed, the element at the current index is in its proper location in the array's sorted portion.

6. The outer for loop iterates through the array until all elements are positioned correctly and the array is completely sorted.

Approach Of Algorithm

1. Assume that the first element in the list is in the sorted part and the rest are in the unsorted component.

2. Take the first element from the unsorted part and insert it into the sorted component in the specified order.

3. Repeat the preceding steps until all of the elements from the unsorted part have been transferred to the sorted portion.

Crack your next tech interview with confidence!

How Insertion Sort Works?

Let's take a look at how the insertion order Algorithm works.

Consider an unsorted array to better grasp how the insertion sort algorithm works. An example will help you comprehend the insertion sort.

Let the array elements be -

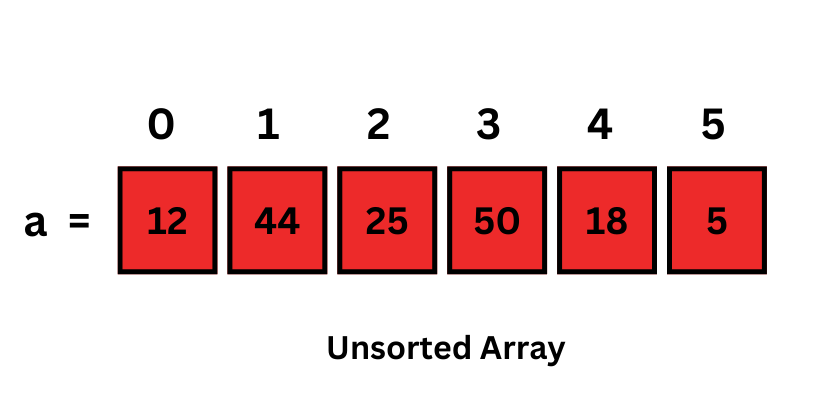
1. The element at index i=0 is 12 and there is no other element on the left of 12. So, currently, the subarray up to the first index is sorted as it contains only element 12.





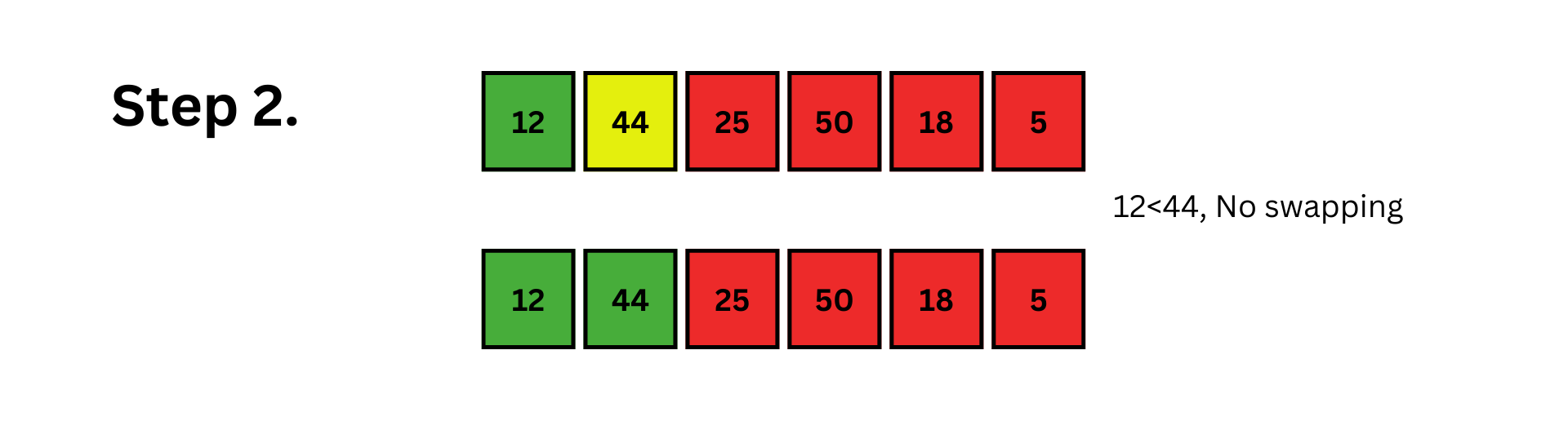
2. The selected element at index i=1 is 44. Now, we will try to move leftwards and put 44 in its correct position. Here, 44 > 12 and so 44 is already in its correct position. Now, the subarray up to the second index is sorted.





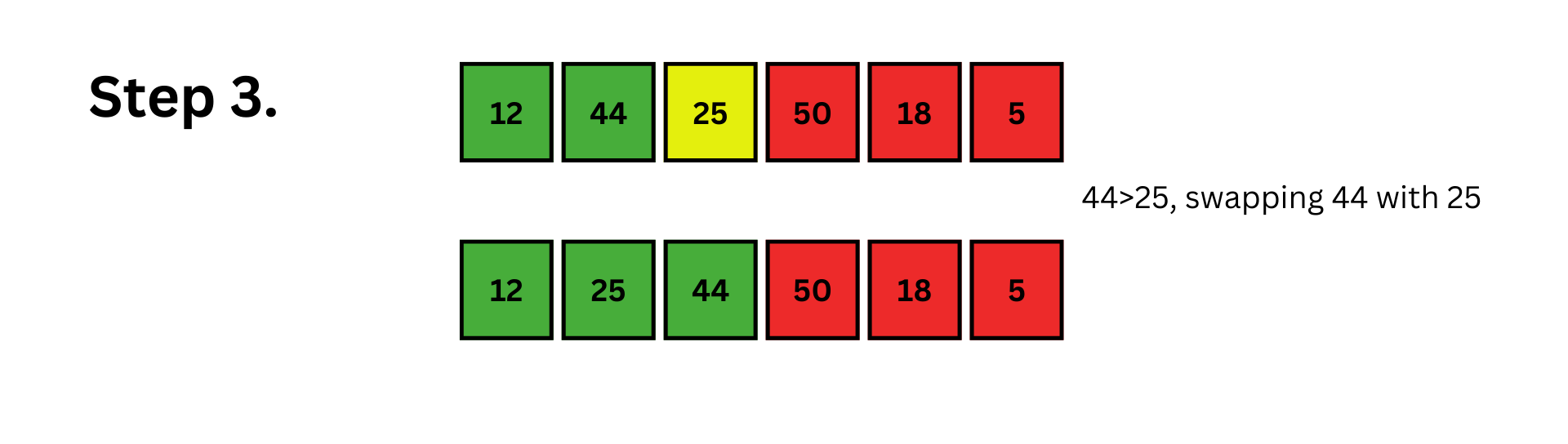
3. The selected element at index i=2 is 25. Now, we will try to move leftwards and put 25 in its correct position. Here, the correct position for 25 will be index 1. So, we will insert 25 in between 12 and 44. We will do it by swapping 25 and 44. Now, the subarray up to the third index is sorted.





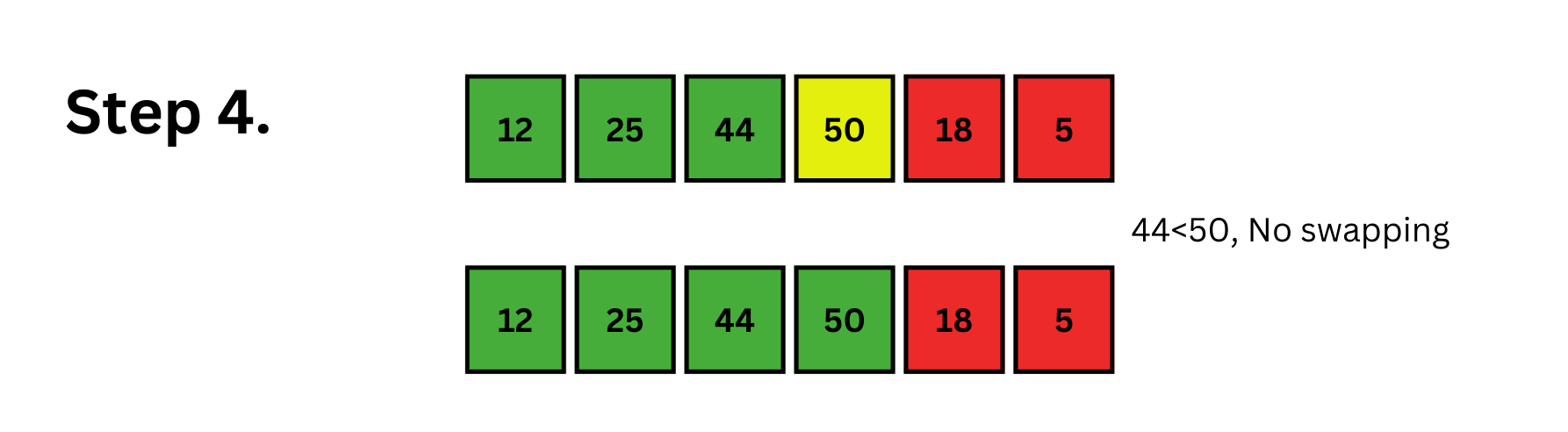
4. The selected element at index i=3 is 50. Now, we will try to move leftwards and put 50 in its correct position. Here, the correct position for 50 will be index 3. So, we need not swap anything. Now, the subarray up to the fourth index is sorted.





5. The selected element at index i=4 is 18. Now, we will try to move leftwards and put 18 in its correct position. Here, the correct position for 18 will be index 1. So, we need to swap adjacent elements until 18 reaches index 1. Now, the subarray up to the fifth index is sorted.





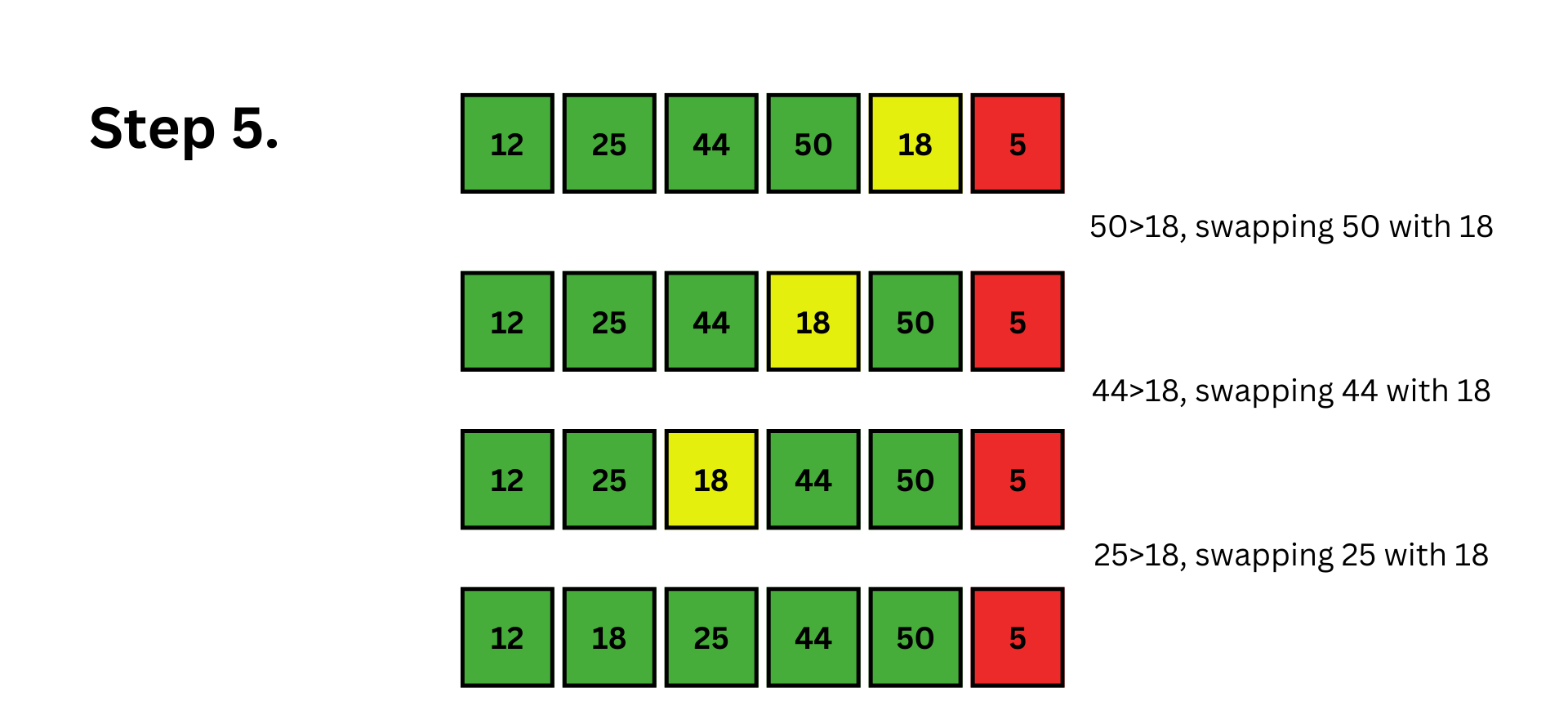
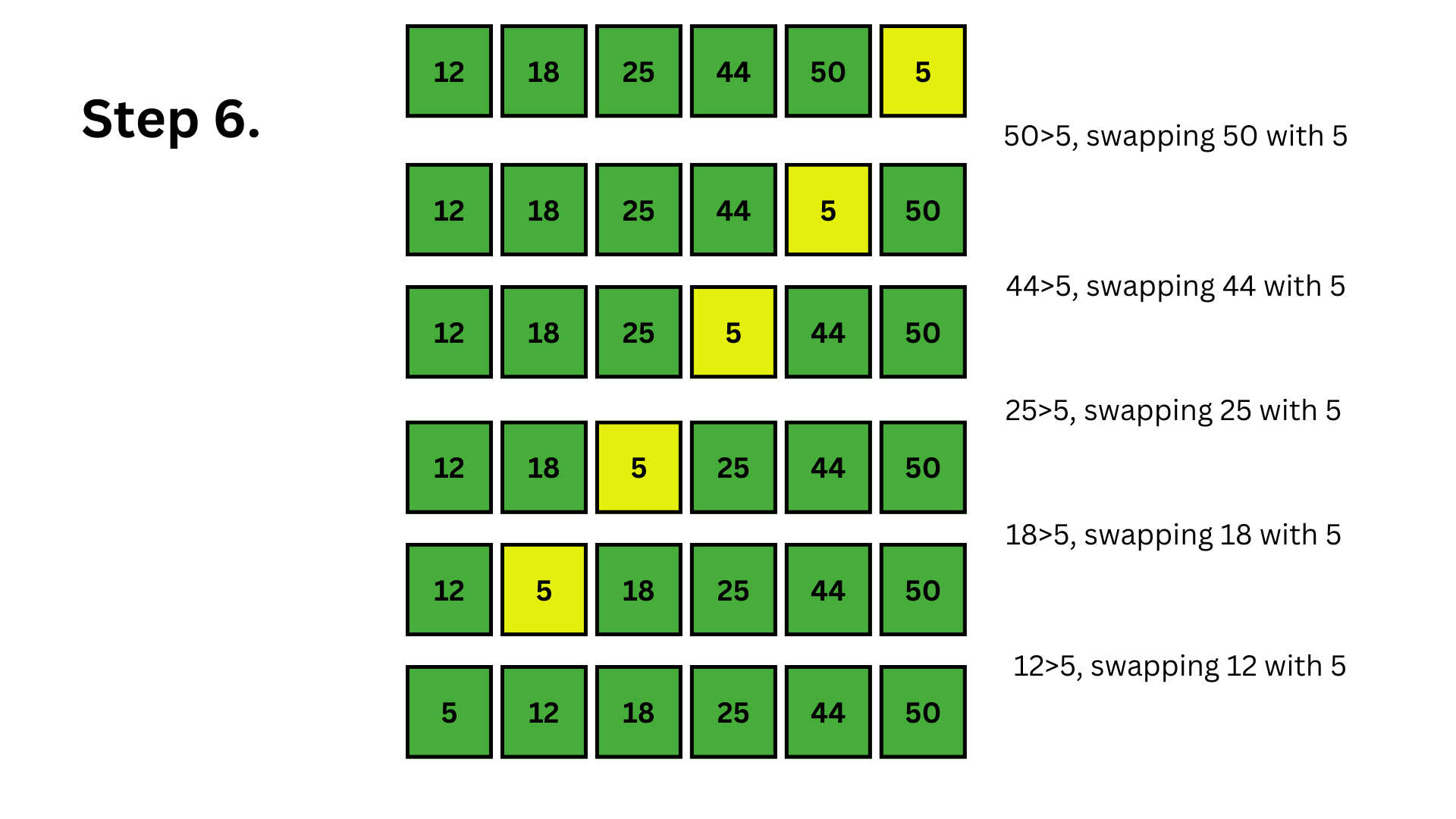
6. The selected element at index i=5 is 5. Now, we will try to move leftwards and put 5 in its correct position. Here, the correct position for 5 will be index 0. So, we need to swap adjacent elements until 5 reaches index 0. Now, the whole array is sorted.

Implementation Of Insertion Sort Algorithm

Implementation Of Insertion Sort In C

#include <stdio.h>

// Function to print an array
void printArray(int arr[], int size) {
  for (int i = 0; i < size; i++) {
    printf("%d ", arr[i]);
  }
  printf("\n");
}

void insertionSort(int arr[], int size) {
  for (int step = 1; step < size; step++) {
    int key = arr[step];
    int j = step - 1;


    while (key < arr[j] && j >= 0) {
      arr[j + 1] = arr[j];
      --j;
    }
    arr[j + 1] = key;
  }
}

int main() {
  int data[] = {12, 44, 25, 50, 18, 5};
  int size = sizeof(data) / sizeof(data[0]);
  insertionSort(data, size);
  printf("Sorted array is :\n");
  printArray(data, size);
}                      

Output

Sorted array is :
5 12 18 25 44 50                  

Implementation Of Insertion Sort In C++

#include<stdio.h>    
#include <bits/stdc++.h>
using namespace std;
 
// Function to sort an array using
void insertionSort(int array[], int n)
{
    int i, key, j;
    for (i = 1; i < n; i++)
    {
        key = array[i];
        j = i - 1;
 
        // Move elements of arr[0..i-1], 
        // that are greater than key, to one
        // position ahead of their
        // current position
        while (j >= 0 && array[j] > key)
        {
            array[j + 1] = array[j];
            j = j - 1;
        }
        array[j + 1] = key;
    }
}

void printArray(int array[], int n)
{
    int i;
    for (i = 0; i < n; i++)
        cout << array[i] << " ";
    cout << endl;
}
int main()
{
    int array[] = {12, 44, 25, 50, 18, 5};
    int N = sizeof(array) / sizeof(array[0]);
 
    insertionSort(array, N);
    cout << "Sorted array is :- \n";
    printArray(array, N);
 
    return 0;
}                  

Output

Sorted array is :- 
5 12 18 25 44 50                   

Implementation Of Insertion Sort In Python

def insertionSort(array):

    for step in range(1, len(array)):
        key = array[step]
        j = step - 1
        
        # Compare key with each element on the left of it until an element smaller than it is found
        # For descending order, change keyarray[j].        
        while j >= 0 and key < array[j]:
            array[j + 1] = array[j]
            j = j - 1
        
        array[j + 1] = key


data = [12, 44, 25, 50, 18, 5]
insertionSort(data)
print('Sorted Array is :')
print(data)                     

Output

Sorted Array is :
[5, 12, 18, 25, 44, 50]               

Implementation Of Insertion Sort In Java

class Main
{
    public static void main(String args[])
    {
        int a[] = {12, 44, 25, 50, 18, 5};

        insertionSort(a);

        System.out.println("Sorted Array is :- ");
        printArray(a);
    }

    /*Function to sort array using insertion sort*/
    static void insertionSort(int arr[])
    {
        int len = arr.length;
        for (int i = 1; i < len; i++) 
        { 
            int temp = arr[i]; 
            int j = i - 1; 

            /* Shift elements of a[i-1 .... 0], that are greater 
            than key, to one position right of their 
            current position */ 
            while (j >= 0 && arr[j] > temp)
            {
                arr[j + 1] = arr[j];
                j = j - 1;
            }
            arr[j + 1] = temp;
        }
    }
    static void printArray(int a[])
    {
        int len = a.length;
        for (int i = 0; i < len; ++i)
            System.out.print(a[i] + " ");
        System.out.println();
    }
}                  

Output

Sorted Array is :- 
5 12 18 25 44 50                  

Implementation Of Insertion Sort In PHP

<?php  
    $a = array( 12, 44, 25, 50, 18, 5 );  
    function printArray($a)
    {
    for($i = 0; $i < 6; $i++)  
    {  
        print_r($a[$i]);  
        echo " ";  
    }      
    }
    for ($i = 1; $i < 6; $i++) 
	{
		$temp = $a[$i];
		$j = $i - 1;
		while($j >= 0 && $temp <= $a[$j])  /* Move the elements greater than temp to one position ahead from their current position*/
        {  
            $a[$j+1] = $a[$j];   
            $j = $j-1;  
        }  
        $a[$j+1] = $temp;  
	}  
    echo "
 Sorted Array is: - 
";  
    printArray($a);
?>  
            

Output

Adress of b is : 8 
Size of Integer b is : 4                  

Time Complexity of Insertion Sort

Insertion sort does two things: it scans the list, comparing each combination of elements, and it shifts the elements if they're out of order. Each action adds to the algorithm's running time.

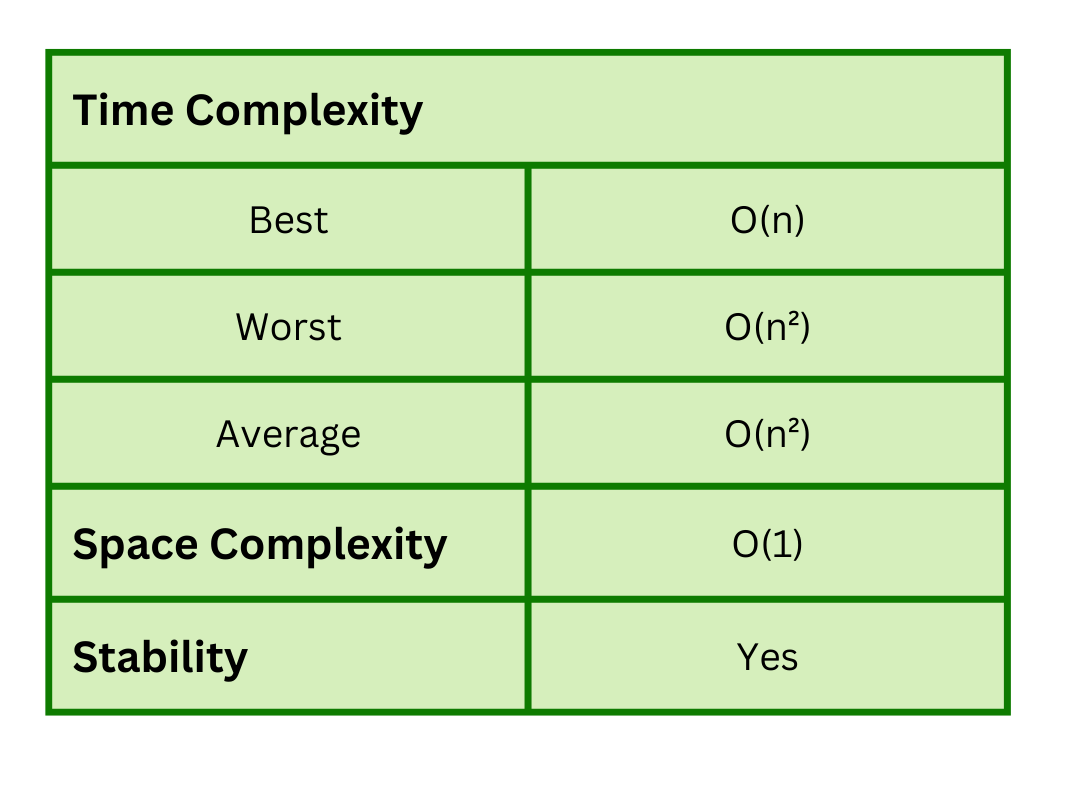
1. Best Case Complexity :- O(n)

   When the array has already been sorted, the outer loop executes n times, while the inner loop does not operate at all. As a result, there are only n similarities. As a result, intricacy is linear.

2. Worst Case Complexity: O(n²)

   Assume you have an array that is sorted in ascending order and want to arrange it in descending order. Worst-case complexity happens in this case.

   Each element must be compared to each of the other elements, resulting in (n-1) evaluations for every nth element. As a result, the overall number of comparisons = n*(n-1) n²

3. Average Case Complexity: O(n²)

   When all of the elements in the provided input array are in jumbled and mixed-up order, i.e. neither ascending nor descending, this is the average case.

Space Complexity of Insertion Sort

Space Complexity of Insertion Sort Algorithm = O(1).

Stability :- Yes

It iterates through each element, extracts it to a variable, and compares it to all of its left components. As a result, the only space consumed is for that variable. Because the algorithm's use of space is independent of the size of the array, it will require the same amount of space regardless of how large or small the given input array is.

Applications Of Insertion Sort

In the following situations, Insertion sort is used:

1. The array has a limited amount of elements.

2. Only a few components remain to be sorted.

Advantages of Insertion Sort

1. Implementation is uncomplicated.

2. Suitable for small data collections

3. It is adaptive, which means it is suitable for data sets that have already been substantially sorted.

Conclusions

This article was not just about the algorithm. We also talked about the algorithm's complexity, operation, and implementation in various computer languages. Insertion Sort is most effective when dealing with a small amount of elements. Insertion Sort has an O(n²) worst-case runtime complexity, comparable to Bubble Sort. However, Insertion Sort is thought to be superior to Bubble Sort

Good luck and happy learning!