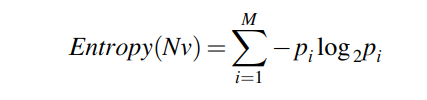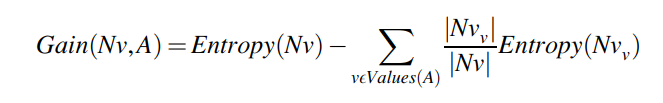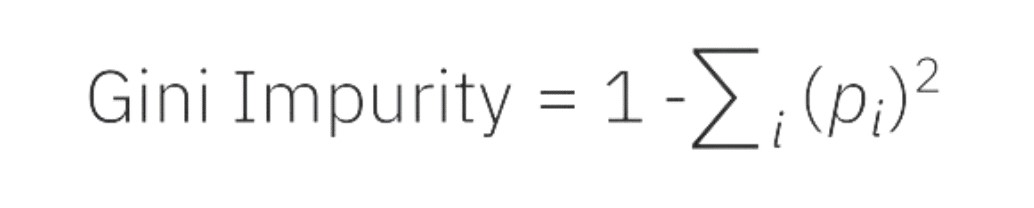Decision Tree in Machine Learning
The decision tree is a type of supervised machine learning approach that makes decisions based on input data. It is a tree-like structure algorithm used to build a model that predicts outcomes based on the provided input data sets. It may be applied to both classification and regression problems. The decision tree works by splitting the dataset into smaller and more manageable subsets based on the feature values, allowing us to navigate through the data and extract valuable insights. Its tree-like structure has internal nodes that represent the features of datasets, the branches represent the decision rules and the leaf node or terminal node represents the final outcome of the tree.
The CART algorithm, which stands for Classification and Regression Tree algorithm, is used to construct a decision tree. It is a graphical depiction for obtaining all possible answers to a choice or problem based on predetermined conditions.
The decision tree consists of two nodes which are the Decision Node and the Leaf Node and only poses a question and divides the tree into subtrees according to the response (Yes/No). Decision nodes are used to make decisions based on the features of the data sets and have multiple branches and the leaf Node represents the prediction of those decisions and does not have any further branches.
So in simple terms, we conclude that in a decision tree, the root node represents the initial decision point or the first feature to split the data, the internal nodes represent the following decision points based on the features that split the data before, and branches of the decision tree represent the decision outcome of each node and lead to the next node and each leaf node represents the final outcome of the decision tree. The below diagram explains the basic structure of the decision tree:
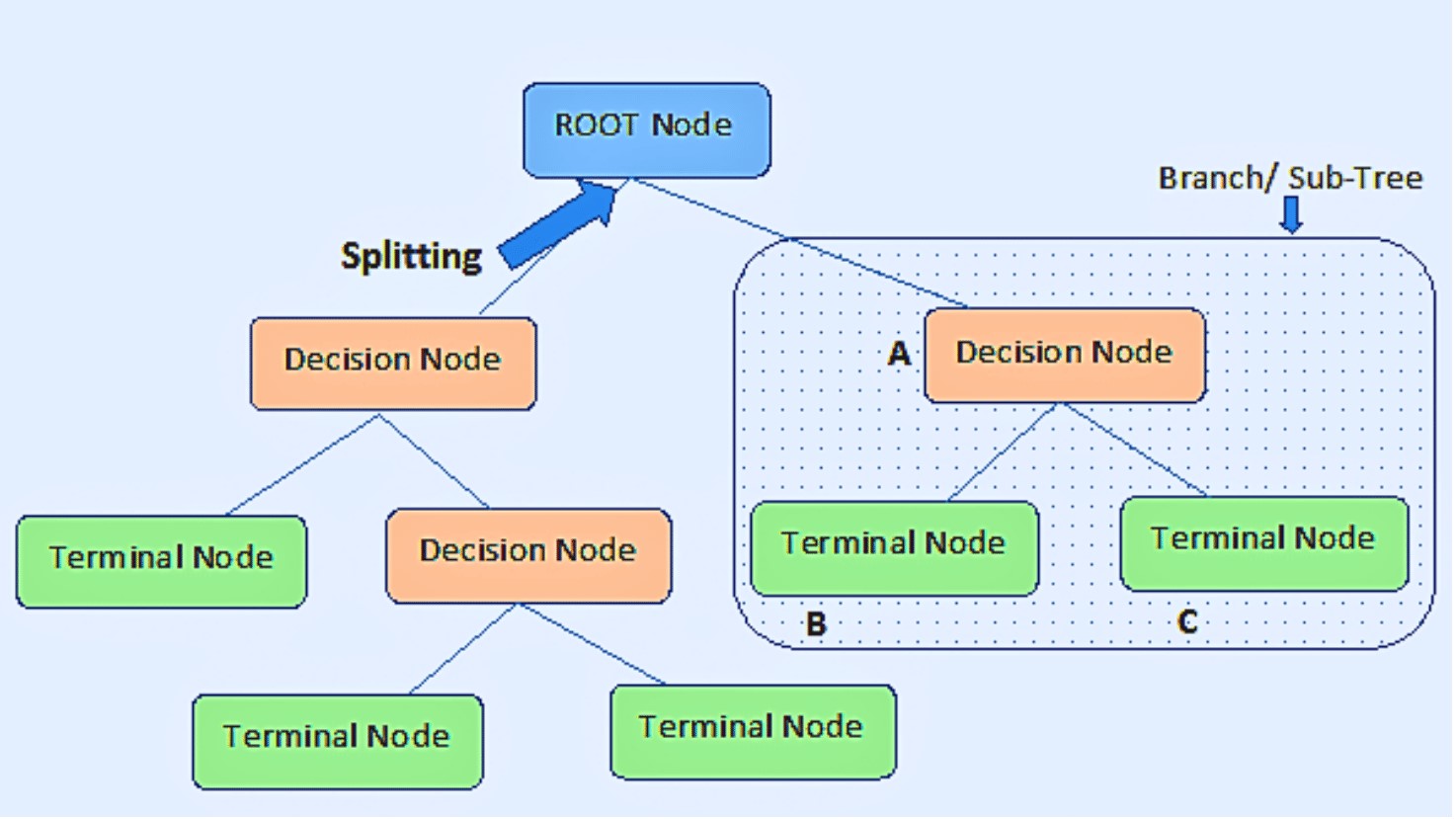
Decision Tree Terminologies:
• Root node: It is the highest node from where the decision tree starts. It represents the entire dataset and from this node, the population begins to divide into groups based on different attributes.
• Decision Nodes (Internal Nodes): The decision Node refers to the nodes obtained after separating the root nodes. It is also called an internal node which is determined by values of a particular attribute.
• Decision Criteria: Decision criteria are the rules that determine how the data should be split at the decision node.
• Leaf Nodes (Terminal Nodes): Leaf nodes or terminal nodes are the nodes where further splitting of trees is not allowed, these are the final output node.
• Splitting: It involves splitting a root node or decision node into two or more smaller nodes based on decision criteria.
• Branches (Edges): Branches are the links between the nodes, these show how the decisions are made.
• Subtree: This decision tree's sub-section formed by splitting the tree is referred to as a sub-tree.
• Pruning:Pruning is the process of removing unwanted nodes or branches from a tree to prevent overfitting.
• Child and Parent Node:A node that has sub-nodes is referred to as the parent node of the sub-nodes, whereas sub-nodes are referred to as the child nodes.
 Learn More️
Learn More️
How Does a Decision Tree Algorithm Work?
In a decision tree, the algorithm begins at the root node and works its way up to forecast the class of the provided dataset. This algorithm follows the branch and jumps to the following node by comparing the values of the root attribute with those of the record (actual dataset) attribute.
The algorithm verifies the attribute value with the other sub-nodes once again for the following node before continuing. It keeps doing this until it reaches the tree's leaf node.
A decision tree algorithm follows these main steps:
Step 1: Selecting the Root Node:The decision tree starts with a root node, say S representing the entire dataset. This node contains all the available data points.
Step 2: Choosing the Best Splitting Attribute: The algorithm evaluates different features and selects the best one to split the data. The splitting attribute is chosen based on the Attribute Selection Measure (ASM) which is Information Gain or Gini Impurity. These metrics quantify the homogeneity or impurity of the data, helping the algorithm decide which feature to split on.
Step 3: Creating Branches and Nodes: Once the best splitting feature is determined, the algorithm creates child nodes or branches from the current node. Each branch represents a possible value or outcome of the selected feature. The root node S is divided into subsets containing the possible values for the selected best attribute.
Step 4: Recursive Splitting: The splitting process is applied recursively to each subset until a stopping criterion is reached. This stopping criterion could be reaching a certain depth, achieving a minimum number of data points in a leaf node, or other predefined conditions.
Step 5: Leaf Nodes and Predictions: When the recursive splitting process reaches the leaf nodes, these nodes represent the final predictions or decisions. For classification tasks, the leaf nodes are assigned a class label based on the majority of data points belonging to a particular class. For regression tasks, the leaf nodes may contain the average or mean value of the target variable.
Example:
Let us understand the various steps involved in the decision tree algorithm with a simple example to predict whether a student will pass or fail the exam based on their Test score, Assignment score, and Homework completion.
Decision Factors:
• Test Score (%)
• Assignment Score (%)
• Homework Completion (%)
The decision tree starts by selecting the Test Score as the root node. It checks if the test score of a student is more than 60% or not. This is the first splitting point of the decision tree. Then the decision tree is split to evaluate the assignment score and check if the assignment score of the student is greater than 50% or not. Then the tree moves forward to assess the homework completion.
Decision Tree steps to predict if a student fails or passes the Exam
1. Root Node: Is Test Score ≥ 60%
• Yes → proceed to the next node (node 2)
• No → Student fails (leaf node)
2. Node 2: Is Assignment Score ≥ 50%
• Yes → Proceed to the next node (node 3)
• No → Student fails (leaf node)
3. Node 3: Is Homework Completion ≥ 50%
• Yes → Pass the exam (leaf node)
• No → Fail the exam (leaf node)
Example Path:
Test Score ≥ 60% → Assignment Score ≥ 50% → Homework Completion ≥ 50% → Pass the Exam.
The decision tree considers various decision factors to predict if the student fails or passes the exam by evaluating their test score, assignment score, and homework completion. The student who meets the expected score of test, assignment, and homework completion passes the exam, the algorithm checks if the student meets all the factors then the student passes the exam otherwise they fail the exam.
The decision tree algorithm works by selecting the best feature to split the data, creating branches and nodes, and recursively splitting until reaching the leaf nodes, which provide the final predictions or decisions. The mathematical formulas for information gain and Gini impurity help in determining the optimal splits during the decision-making process.
Assumptions while Using Decision Tree
Some of the assumptions we make when using Decision Tree are as follows:
• Training set: Initially, the entire training set is regarded as the root.
• Categorical Features: Categorical feature values are desired. If the data are continuous, they are discretized before the model is built.
• Record Distribution: Recursively, records are dispersed based on attribute values.
• Attribute Selection: A statistical technique is used to select attributes for root nodes and sub-nodes.
• Disjunctive Normal Form: Decision trees are based on the Sum of Product (SOP) representation. Disjunctive Normal Form is another name for the Sum of Product (SOP). Every branch from the tree's root to a leaf node with the same class represents a conjunction (product) of values, whereas distinct branches ending in that class create a disjunction (sum).
• Attribute Selection Measures: The main factor in implementing the decision tree is determining which traits should be considered as the root node at each level. Handling this is referred to as attribute selection. The two attribute selection techniques are:
1. Information Gain
2. Gini Index
Attribute Selection Measures
The biggest challenge that emerges while creating a Decision tree is how to choose the optimal attribute for the root node and sub-nodes. To tackle such challenges, a strategy known as Attribute selection measure, or ASM, is used which is commonly performed using these techniques:
1. Entropy
2. Information Gain
3. Gini Index
Entropy in Decision Trees:
Entropy is a fundamental concept in information theory that measures the amount of uncertainty or impurity in a given set of data. It provides a way to quantify the level of disorder or unpredictability in a system. The dataset in the decision tree is split based on the feature value for each data point. If the data points belong to the same class then the entropy will be 0 that is there will be no disorder. If the data point is split evenly between classes, then the entropy will be high that is there will be maximum disorder. The higher entropy will make it harder to make predictions. When the data is mixed or uncertain, the entropy will be high, and with uniform data entropy is low.
Entropy Formula:
The entropy of the dataset S is represented as the summation of the negative probabilities of each class i in S multiplied by the algorithm of these probabilities and is mathematically represented as:
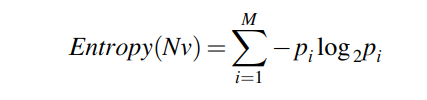
Where:
• Entropy(Nv) = Entropy of the dataset S.
• ∑ = represents the summation of all classes or categories i present in the dataset S.
• p(i) = Represent the probability of data points belonging to a particular class or category i.
Example 1:
Let's explore entropy in more detail, using a simple example and the relevant mathematical formula. Imagine we have a dataset of animal species and their corresponding color: red, blue, and green. Let's assume we have 100 animals in total, with the following distribution:
| Color |
Number of Animals |
Probability |
| Red |
40 |
0.4 |
| Blue |
30 |
0.3 |
| Green
|
30 |
0.3 |
Calculating Entropy
Entropy(S) = - [p(red) * log2*p(red) + p(blue) * log2*p(blue) + p(green) * log2*p(green)]
Entropy(S) = - [(40/100) * log2(40/100) + (30/100) * log2(30/100) + (30/100) * log2(30/100)]
Entropy(S) = - [(0.4 * log2(0.4)) + (0.3 * log2(0.3)) + (0.3 * log2(0.3))]
Entropy(S) ≈ - [(-0.528) + (-0.521) + (-0.521)]
Entropy(S) ≈ - (-1.570)
Entropy(S) ≈ 1.570
Interpretation
The entropy value for this dataset is approximately 1.570, representing the uncertainty in predicting the color of an animal. The animals are distributed among different colors, but there is no dominant color, the entropy value of approximately 1.570 indicates moderate uncertainty.
Entropy ranges from 0 to 1. A value of 0 indicates complete order or certainty, where all the data points belong to the same class. On the other hand, a value of 1 indicates complete disorder or randomness, where the data points are evenly distributed across different classes.
Example 2:
Now, let's consider another example where all the animals in the dataset are of the same color. Suppose we have 100 red animals. In this case, the entropy calculation would be as follows:
Entropy(S) = - [(100/100) * log2(100/100)]
Entropy(S) = - [1 * log2(1)]
Entropy(S) = - [0]
Entropy(S) = 0
In this scenario, the entropy value is 0, indicating complete order or certainty. Since all the animals are of the same color, there is no uncertainty or randomness.
Information Gain:
Information gain is a key concept used in decision tree algorithms to determine the best feature to split the data. It measures the reduction in entropy or uncertainty achieved by splitting the data based on a specific attribute. The attribute that yields the highest information gain is considered the root node. Information gain is used to decide the splitting criterion at each step while building a decision tree.
To calculate the information gain, we compare the entropy of the original dataset with the weighted average of the entropies of the subsets created by the attribute split. We need to consider the entropy of the dataset before and after the split.
Information Gain Formula:
The formula for information gain of attribute A with respect to node Nv in the decision tree quantifies how much attribute A contributes to reducing the entropy or uncertainty at node Nv. The formula is presented as:
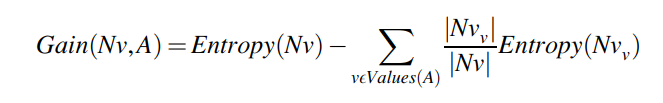
Where:
• Gain(Nv, A) = Represents the information gained by splitting the node Nv using attribute A.
• Entropy(Nv) = The entropy of the entire dataset.
• ∑ = Summation of all the possible values v an attribute A can take.
• Nvv = Represents the subsets created by splitting the dataset Nv based on attribute A.
• |Nvv| and |Nv|= Denotes the number of instances in the subset Nvv and the original dataset Nv, respectively.
• Entropy(Nvv) = Represents the entropy of each subset Nv.
Example:
Let's use the previous example of animal species and their colors to illustrate the calculation of information gain. Assuming we want to determine the attribute that best separates the animals based on their colors, we can consider attributes like "age" and "habitat." Let's calculate the information gain for both attributes:
Information Gain for attribute Age:
Subset 1:
| Color |
Number of Animals |
Age |
| Red |
40 |
<=10 years |
| Blue |
20 |
<=10 years |
| Green
|
0 |
<=10 years |
Subset 2:
| Color |
Number of Animals |
Age |
| Red |
0 |
>10 years |
| Blue |
10 |
>10 years |
| Green
|
30 |
>10 years |
Calculating Entropy for subset 1 (age<=10):
Entropy(Subset1) ≈ - [(40/60) * log2(40/60) + (20/60) * log2(20/60) + (0/60) * log2(0/60)]
Entropy(Subset1) ≈ - [0.67*log2*0.67 + 0.33*log2*0.33 + 0*log2*0]
Entropy(Subset1)≈0.91
Calculating entropy for subset 2 (age>10):
Entropy(Subset2) ≈ - [(0/40) * log2(0/40) + (10/40) * log2(10/40) + (30/40) * log2(30/40)]
Entropy(Subset1) ≈ - [0*log2*0 + 0.25*log2*0.25 + 0.75*log2*0.75]
Entropy(Subset1)≈0.811
Overall entropy has already been calculated and it is approximately equal to 1.572
Information Gain (Age)
Information gain (S, Age)= Entropy(S)- Weighted Average
Information Gain = Entropy(S) - [(60/100) * Entropy(Subset1) + (40/100) * Entropy(Subset2)]
Information Gain= 1.572 - [(60/100) * 0.91 + (40/100) * 0.81]
Information Gain=0.702
Information Gain for attribute Habitat:
Subset 1:
| Color |
Number of Animals |
Habitat |
| Red |
40 |
Forest |
| Blue |
10 |
Forest |
| Green
|
0 |
Forest |
Subset 2:
| Color |
Number of Animals |
Probability |
| Red |
30 |
Ocean |
| Blue |
10 |
Ocean |
| Green
|
10 |
Ocean |
Calculating Entropy for subset 1 (Forest):
Entropy(Subset1) ≈ - [(40/50) * log2(40/50) + (10/50) * log2(10/50) + (0/50) * log2(0/50)]
Entropy(Subset1) ≈ - [0.8*log2*0.8 + 0.2*log2*0.2 + 0*log2*0]
Entropy(Subset1)≈0.722
Calculating entropy for subset 2 (Ocean):
Entropy(Subset2) ≈ - [(30/50) * log2(30/50) + (10/50) * log2(10/50) + (10/50) * log2(10/50)]
Entropy(Subset1) ≈ - [0.6*log2*0.6 + 0.2*log2*0.2 + 0.2*log2*0.2]
Entropy(Subset1)≈1.371
Overall entropy has already been calculated and it is approximately equal to 1.572
Information Gain (Habitat)
Information gain (S, Habitat)= Entropy(S)- Weighted Average
Information Gain = Entropy(S) - [(50/100) * Entropy(Subset1) + (50/100) * Entropy(Subset2)]
Information Gain= 1.572 - [(50/100) * 0.722 + (50/100) *1.371]
Information Gain=0.1106
Final Results
Overall Entropy: 1.572
Information Gain for Age: 0.702
Information Gain for Habitat: 0.1106
With the calculated infomation gain for both the attributes that is Age and Habitat, we can determine that the Age attribute has the highest information gain which states that the Age attribute has more information features as compared to habitat and is considered first for splitting the dataset.
Please note that the calculations for entropy and information gain in this example are approximations, as the actual values were not provided. However, this example illustrates the general process and formula used to calculate information gain.
Gini Index:
The Gini index may be thought of as a cost function that evaluates dataset splits. The attribute with the lower Gini index is chosen to split first. It is determined by deducting one from the total of the squared probability for each class. In contrast to information gain, which promotes smaller divisions with unique values, it favors bigger partitions and is simpler to implement.
The frequency with which a randomly selected element will be incorrectly detected is gauged by the Gini Index. When using the CART (Classification and Regression Tree) technique to create a decision tree, the Gini index is a purity or impurity indicator. It is preferable to have an attribute with a low Gini index than one with a high Gini value.
Gini Index calculation formula:
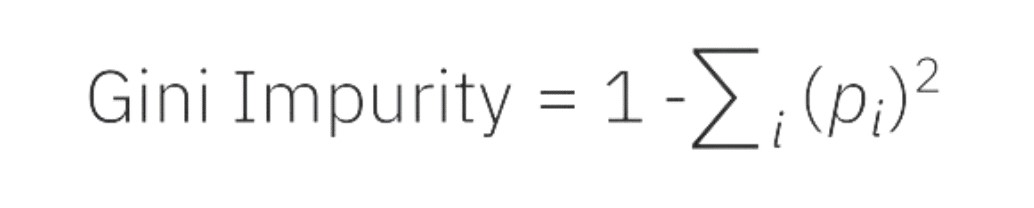
In decision trees and other machine learning techniques, the Gini Index is a typical way to assess inequality or impurity in a distribution. From 0 to 1, where 0 denotes perfect equality (all values are the same), and 1 denotes perfect inequality (all values are different), the scale runs from 0 to 1.
It is computed by adding up the squared probability of each result in a distribution, then taking the sum and subtracting it from 1.
A distribution that is more homogenous or pure has a lower Gini index, whereas a distribution that is more heterogeneous or impure has a higher Gini index. By comparing the impurity of the parent node with the weighted impurity of the child nodes, the Gini Index is used in decision trees to assess the quality of a split.
What are different types of Decision Tree?
The majority of models are used in one of the two primary machine learning paradigms,
supervised or unsupervised machine learning. The supervised machine learning method employs decision trees. There are primary two types of decision trees that are Regression trees and classification trees. Depending on the kind of target variable we have different decision trees can be used, it comes under two variety that is:
1. Decision Tree using Categorical Variables
2. Decision Tree of Continuous Variables
Classification Tree
Classification decision tree is used to solve problems with classification, the target variable is categorical. The model is trained to determine if the input data belongs to a specific class of objects. The output are the class labels which are usually “Yes” or “No”.
The classification model process labeled training data to learn the classes. The entire dataset is divided into smaller subgroups to create a classification tree. The class labels are the end points of the tree branches, these branches are based on the yes or no response. A few examples of classification decision trees are:
• Classifying if the Email is "SPAM" or "HAM"
• Classifying whether to “GO OUT” or “STAY IN” based on the weather condition
• Determining whether to “BUY” or “DON’T BUY” a house based on the age and income of a person.
Regression Decision Tree
Regression problems occur when models are intended to predict the continuous value based on previous information or data sources, such as forecasting changes in stock values or home prices. It is a method for teaching a model how independent variables and a result relate to one another. Regression models are under the category of supervised machine learning algorithms since they will be trained using labeled training data.
The model may be used to predict results from unknown input data by establishing the connections. The model plots a graph with the input features and target variable and tries a fit a line through these data points to minimize the difference between the actual value and the predicted values. These models may be used to not only fill in the gaps in the historical data but also to forecast future or emerging patterns in a variety of scenarios. Regression models may be used in machine learning for tasks such as:
• Predict the house price using data points of prices in the previous years.
• Predict the employee's salary based on their experience year, education level, or position.
Decision Tree Algorithms in Machine Learning:
1. ID3 (Iterative Dichotomiser 3):This algorithm is primarily used for classification and handles categorical datasets. The algorithm builds the tree from the provided datasets by selecting the attribute with the highest information gain. They use the Entropy and Information Gain techniques to assess the potential split for creating subgroups with the same classes.
2. C4.5: This algorithm, which was created by Quinlan along with ID3, is regarded as its successor. It is an improvement of the ID3 algorithm usually used for classification tasks and handles real-world data with more robustness. The algorithm uses the Information Gain and Gain Ratio for evaluating the split points inside the decision tree. It can handle the continuous and categorical attributes and avoid biasedness towards features with many levels, handle missing values, and avoid overfitting.
3. CART (Classification and Regression Trees): CART was introduced by Leo Breiman, it handles both the classification and regression trees. Gini impurity is often used by this method to choose the best characteristic to split on, it determines how often a randomly chosen attribute can be misclassified and minimizes the least squared error at each node to find the most optimal solution. A lower number is preferable when using Gini impurity to evaluate.
4. CHAID (Chi-squared Automatic Interaction Detector): This algorithm performs multi-level splits at each node when computing classification trees making it ideal for decision trees with multiple categories. It split the data by performing chi-square tests to determine the best relationship between the independent variable and the target value.
Why do we use Decision Trees?
A decision tree is considered one of the best approaches to solving machine learning problems due to several compelling reasons as outlined below:
• Mimicking Human Thinking: The process of decision-making in a decision tree resembles the human thinking process. They are structured in the way how humans solve problems by breaking down complex problems into smaller manageable steps. This makes the understanding and interpretation process easy.
• Interpretability:The tree-like structure of the decision tree provides a high level of interpretability. The structure provides a clear and transparent approach to a solution, this helps the user to easily understand how the attributes and conditions lead to each decision by tracing the path from the root to the leaf node.
• Handling Nonlinear Relationships:Decision trees can handle the non-linear relationship between variables by portioning the entire dataset into a subset of different features, this helps in making accurate predictions based on the various patterns.
• Feature Selection: Decision trees perform feature selection by giving more significance to the features with higher importance and less importance to irrelevant features. This feature selection ability of a decision tree improves model performance and reduces the problem dimensionality by focusing more on relevant attributes.
• Handling Missing Values and Outliers: Decision trees can handle missing values and outliers in the data without significant pre-processing. Missing values can be handled by assigning the majority class or the class with the highest frequency in the parent node. Outliers do not heavily affect the decision tree's performance, as the algorithm works by splitting the data based on thresholds and conditions.
• Ensemble Methods: Decision trees can be combined using ensemble methods like random forests or gradient boosting. These techniques involve training multiple decision trees and aggregating their predictions to make the final decision. Ensemble methods enhance the performance and robustness of decision tree models by reducing overfitting and increasing generalization.
Decision Tree Real-Life Example
Imagine you are a loan officer at a bank, and your task is to determine whether a loan applicant is likely to default or not. You have a dataset containing
information about previous loan applicants, including attributes such as age, income, employment status, credit score, and loan amount. Your goal is to build a
decision tree model that can accurately predict the likelihood of loan default.
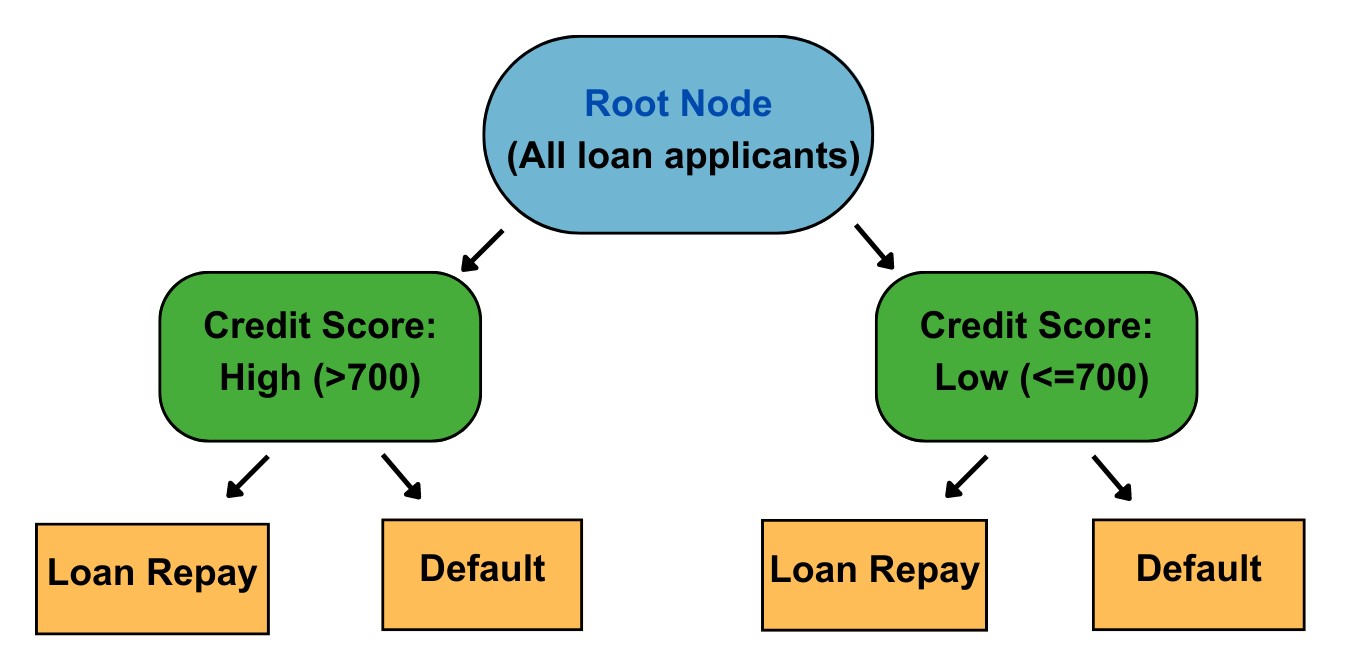
• To begin, you analyze the dataset and identify the target variable, which in this case is whether the loan applicant defaulted or not. This will serve as the basis
for making predictions. Next, you select the most relevant features from the dataset, such as income, credit score, and employment status, which can potentially
impact the loan repayment ability.
• The decision tree algorithm starts with a root node, representing the entire dataset. It then evaluates different features to determine the best split that
maximizes the information gain or reduces the impurity in the data. For example, it may find that splitting the data based on credit score yields the highest
information gain.
• The algorithm creates branches based on the credit score values, such as "high credit score" and "low credit score." Each branch represents a subset of the data
that satisfies the condition. It then continues recursively, evaluating different features at each internal node and splitting the data into smaller subsets based
on the selected features.
• In our example, the decision tree may further split the data based on income and employment status. It may create branches such as "high income and employed,"
"low income and employed," and "unemployed." These branches represent different subsets of the data with distinct characteristics.
• As the algorithm continues to split the data, it eventually reaches the leaves of the tree, which represent the final predictions or decisions. In our loan default
example, the leaves may represent "likely to default" and "likely to repay." The decision tree model has learned patterns and relationships within the dataset,
enabling it to make predictions on new loan applicants based on their attributes.
• Now, when a new loan applicant comes in, you can input their information into the decision tree model. The model will traverse the tree, following the branches
based on the applicant's attributes, until it reaches a leaf node and provides a prediction whether the applicant is likely to default or not.
• By using decision tree machine learning in this loan default scenario, you can effectively assess the risk associated with granting loans to different applicants.
This model provides transparency and interpretability, as you can trace the decision path within the tree and understand how various factors contribute to the final
prediction.
Applications of Decision Tree
1. Credit Scoring:
Decision tree is widely used in banking and finance for credit scoring. The decision tree model analyzes the customer data, including their employment history, income, credit history, and other relevant data. The model evaluates various factors to assess the applicant's creditworthiness and determine the risk before granting the loan.
2. Medical Diagnosis:
A decision tree is employed in the medical field to predict the patient's diagnosis by analyzing their symptoms, medical history, and test results. The tree assists doctors in providing them the suitable treatment plans and suggesting accurate diagnoses with previous patient information.
3. Customer Churn Prediction:
Decision tree models are valuable for predicting client loss in customer relationship management. By examining customer demographics, purchase history, engagement metrics, and other relevant data, decision trees can identify patterns and factors that contribute to client turnover.
4. Fault Diagnosis in Engineering:
Decision tree is used in engineering for diagnosing faults in complex systems. Decision trees can detect the root cause of the fault in machines by analyzing the system parameters, sensor data, and historical performance. This assists engineers in the maintenance, repair, and adjustment of machinery for optimal functioning.
Advantages of decision trees in machine learning
• Easy to comprehend and interpret: The decision tree approach of visualizing the decision-making process makes it easy to understand even for non-technical stakeholders.
• Versatility: Decision trees are capable of working with both categorical and numerical data, making them versatile.
• Handle missing values: Decision trees are capable of handling missing values, it does not affect the tree-making process to any considerable extent.
• No need for data normalization or scaling: The decision tree does not require normalization and scaling of data as it is based on the hierarchical splitting of feature
• Non-linear relationship: The decision tree can handle non-linear relationships between attribute and target value without any complex transformation.
Disadvantages of decision trees in machine learning
• Overfitting: Decision trees develop into highly complicated and large structures may lead to overfitting. Pruning is necessary in decision trees to avoid overfitting.
• High Variance: Even slight changes in the data might produce an entirely different tree, decision trees can be unstable.
• Greedy nature: the greedy nature of the decision tree results in suboptimal solutions with high-dimensional datasets.
• Biased: A decision tree with an imbalanced dataset behaves biased towards the dominant class leading to poor performance towards the minority class.
How to avoid Overfitting in Decision Trees?
The usual difficulty with decision trees is that they fit a lot, especially in tables with many columns. The training data set may appear to have been remembered by
the tree at times. A decision tree will provide 100% accuracy on the training data set if no limits are placed since, in the worst scenario, it will produce one leaf
for each observation. As a result, this influences the precision of predictions for samples that are not included in the training set.
Overfitting is a common challenge in decision tree models, where the model becomes too complex and specific to the training data, resulting in poor generalization
to unseen data. To avoid or counter overfitting in decision trees, two effective techniques are pruning and using random forests.
1. Pruning Decision Trees:
Pruning is a technique used to reduce the complexity of a decision tree by removing unnecessary branches and nodes. It helps prevent overfitting and improves the model's ability to
generalize to new data. Two popular pruning methods are pre-pruning and post-pruning.
• Pre-pruning: In pre-pruning, the decision tree is grown by setting constraints on the tree's size and depth during the learning process. Common pre-pruning techniques include:
• Setting a maximum depth for the tree
• Setting a minimum number of samples required to split a node
• Setting a maximum number of leaf nodes
• Post-pruning: In post-pruning, the decision tree is grown to its maximum size and then pruned by removing branches that do not significantly improve the model's performance on
validation data. Common post-pruning techniques include:
• Cost complexity pruning (also known as alpha pruning or weakest link pruning): This method assigns a cost parameter to each subtree and selects the subtree with the minimum cost. The
cost is determined by considering the model's accuracy and complexity.
• Reduced error pruning: This approach evaluates the impact of pruning a node by comparing the error rate before and after pruning. If the pruning leads to a decrease in error rate, the
subtree is removed.
2. Random Forest:
Random Forest is an ensemble learning method that utilizes multiple decision trees to make predictions. It helps mitigate overfitting by combining the predictions of several trees and
reducing individual tree biases. Here's how it works:
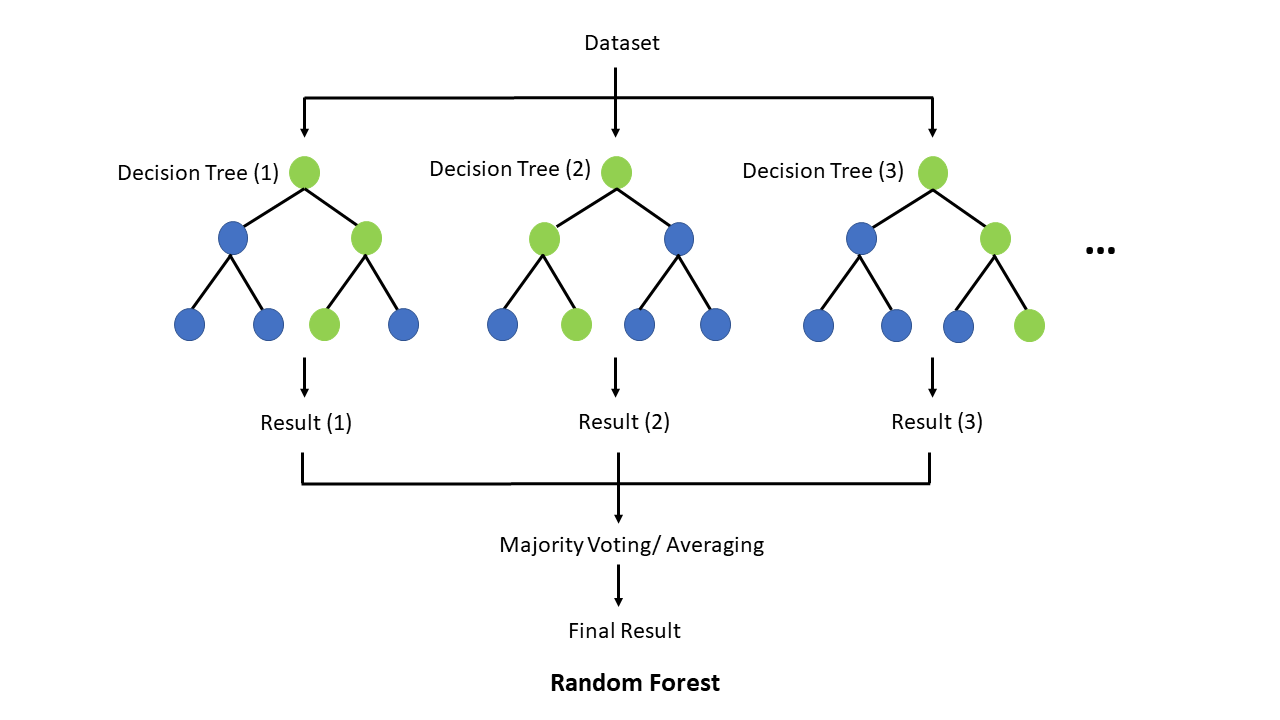
• Randomly select subsets of the training data with replacement (bootstrapping).
• Build a decision tree on each subset with a random selection of features.
• Predict the outcome by aggregating the predictions of all the trees (e.g., majority voting for classification or averaging for regression).
Random Forest improves generalization by reducing the impact of individual decision trees that may overfit the training data. By averaging predictions from multiple trees, it reduces
bias and variance, leading to better overall performance on unseen data.
Example:
Let's consider a scenario where we have a decision tree model for classifying emails as spam or not spam based on various features. If the model is overfitting, it may create complex
branches and nodes that memorize the training data, leading to poor performance on new email samples.
To counter overfitting, we can apply pruning techniques. For instance, we can set a maximum depth limit for the tree, such as 5 levels. This constraint prevents the tree from becoming
overly complex and improves generalization. Additionally, we can use cost complexity pruning, which assigns costs to subtrees based on their performance on validation data, and prunes
subtrees with higher costs.
Alternatively, we can employ a random forest approach. We create an ensemble of decision trees, each trained on a random subset of the training data and a random selection of features.
By aggregating the predictions of multiple trees, we can achieve better accuracy and reduce overfitting.
By using pruning techniques or employing random forest, we can effectively counter overfitting in decision tree models and improve their generalization capabilities to unseen data.
Conclusions
In conclusion, decision tree machine learning is a potent method that may simplify the difficulties of data processing and facilitate efficient decision-making.
It is a useful tool in many disciplines due to its interpretability, capacity to handle nonlinear connections, and feature selection skills. You may use decision trees
to get important insights from your data by comprehending how they function and how they are used.
Powerful methods for data classification and assessing the costs, risks, and possible rewards of ideas are decision tree algorithms. You may use a decision tree to
make bias-free decisions in a methodical, fact-based manner. The outputs offer choices in a manner that is simple to understand, making them applicable in a variety
of settings.
Good luck and happy learning!



 Logicmojo
Logicmojo